◎正当な理由による書き込みの削除について: 生島英之とみられる方へ:
高校数学の質問スレPart399 YouTube動画>1本 ->画像>13枚
動画、画像抽出 ||
この掲示板へ
類似スレ
掲示板一覧 人気スレ 動画人気順
このスレへの固定リンク: http://5chb.net/r/math/1548693213/
ヒント:5chスレのurlに http://xxxx.5chb.net/xxxx のようにbを入れるだけでここでスレ保存、閲覧できます。
987 名前:132人目の素数さん [sage] :2019/01/29(火) 02:05:23.17 ID:JRDBFB+4
(4)は判別式から当てはまるa, bは54通りの間違いでした。
54/6・36で答えは1/4でどうでしょうか?
答えは合っていません。
54通りと、54/6がなぜ出てきたのでしょう。
1の容器に1200gの食塩水が、2には600gの水。1の食塩水の半分を2へいれ、次に2の容器の200gわ1に戻したら1の濃度は7%になった。はじめの1の食塩水の濃度は?

この問題の「カ」はどうやるのがベストですか?
>>7 うまい方法なんてあるのかな?
愚直にやるだけなんじゃ?
>>6 初期状態
食塩水1:溶質12x[g]、溶液1200[g]、濃度x[%]
食塩水2:溶質0[g]、溶液600[g]、濃度0[%]
1回目の操作後
食塩水1:溶質6x[g]、溶液600[g]、濃度x[%]
食塩水2:溶質6x[g]、溶液1200[g]、濃度x/2[%]
2回目の操作後
食塩水1:溶質7x[g]、溶液800[g]、濃度7[%]
食塩水2:溶質5x[g]、溶液1000[g]、濃度x/2[%]
7x/800=7/100
要するに、ある濃度の食塩水600グラム(A)に濃度が半分の食塩水200グラム(B)加えたら濃度7%になったということ
Aに食塩がaグラムだとするとBにはa*1/6グラムの食塩が入っている
従って出来上がった食塩水にはa*7/6グラムの食塩が入っている
BがAと同じ濃度の食塩素であった場合は出来上がる食塩水はAの濃度と当然同じであるがここにはa*8/6グラムの食塩が入っている
同じ量の食塩水にa*7/6グラムの食塩が入っている場合が7%なのであるからa*8/6グラム入っている場合なら8%
つまりAの食塩水は8%
面積図みたいなもので考えれば簡単
(問題)7人の内5人を選ぶ時の場合の数を答えよ。
これは計算式として
7C5= 7×6×5×4×3 =21
--------
5×4×3×2×1
こうなると思うんだけど、
実際に選び方を羅列してみると19個しか思いつかないんだけど、
他にどんな選び方があるんだ?
1-2345,2346,2347 2356,2357 2367
2456,2457 2467
2567
3456,3457
3567
4567
2-3456,3457
3567
4567
3-4567
知っていると思うけど選ばない2人を選ぶと考えれば7C5=7C2で計算が楽
数え上げるときも楽
1-2~7……6通り
2-3~7……5通り
・
・
6-7……1通り
なので6+5+4+3+2+1=21
>>12 1、3、4、6、7
と2、3、4、6、7が抜けてると思ったら、だれかがすぐ答えたはるわ。
角Aと角Cが直角で、角Bが鋭角である四角形ABCDにおいて、
Aから辺BCに下した垂線の足をP、Cから辺BAに下した垂線の足をQとする。
このときPQ⊥BDを示せ。
この問題で、ベクトルで考えて内積計算をシコシコやって解いたのですが
初等幾何で証明する方法はできますか。よければ教えて下さい。
>>17 からBDにおろした垂線の足をK、
LからBDにおろした垂線の足をLとおく。
△BADと△BMKは相似だから
BK = BQ (BA/BD) = BC (BQ/BC) (BA/BD) = BA・BC/BD (BQ/BC)。
同様に
BL = BA・BC/BD (BP/BA)。
ここで△BQCと△BPAも相似だから
BM = BA・BC/BD (BQ/BC) = BA・BC/BD (BP/BA) = BN。
∴PQ⊥BD。
長さ60㎝の針金で長方形を作る。面積が最大のとき何㎝2か。
縦をx横をyにして、
2x+2y=60
x+y=30 とし、14・16 13・17と計算しましたが、答えは225㎝*2でした… 長さが15㎝なら長方形でなく正方形じゃないですか?
>>19 正方形が長方形の特別な場合であることは義務教育で学んでいるはず
>>18 点の定義がめちゃくちゃ過ぎてよくわからんw
>>21 ところが2の問題で長方形は「え、か、く」と答えると×にする教師がいるんですよ
問題貼るの忘れた

こっちは解答もあげられていた


正三角形を二等辺三角形とすると×
小学校は学問ではなくて社会性を身に付ける場だろう
空気を読めということ
×に納得いかない優秀な子は抗議に行ってもいいし教師を当てにせずに自分でやってもいい
まぁ小学校の学校の成績なんてクソほどどうでも良くて痛くも痒くも無いだろう
空気を読むことを教えて才能を潰す所
日本じゃ当たり前だね
100円玉3枚、10円玉4枚、1円玉2枚がある。お釣りをもらうことなく支払うことができる金額は何通りか。0円は考えない。
3*4*2でなく、なぜ3+1)*(4+1)*(2+1)マイナス1になるんですか?
>>29 実際に何通りあるか数えてごらんよ
この手の法則は自力で見つけ出したほうが身に付く
数を減らして考えると楽
百円玉1枚、十円玉1枚だったらどうなるか
あと、その問題では大丈夫だが枚数が多くなれば組み合わせは違うんだけど同じ金額になってしまう場合が生じるのでそれを勘案する必要が出てくる
大きい金額から考えると、
342円、341円、340円、
332円、331円、330円、
322円、321円、320円、
312円、311円、310円、
302円、301円、300円、
というふうに、
300円以上だけで、3×5=15通りある。
200円台も100円台も15通りあるが、100円未満だけ14通りになる。
∵0円は除くから。
よって式を書くなら、
3×5×4-1=59(通り)
点F(6,0)からの距離PFと、y軸との距離の比の値PF/PHが2である点P(x,y)の軌跡をもとめよ。また、点Fは軌跡が曲線の焦点の1つとなっていることを示せ
解けるかたお願いします
至急でたのます
双曲線や円錐曲線の定義のまんまやないか
教科書で充分
前
>>33 >>34 Fとおって傾き±1/2やないかな?
y=±(1/2)(x-6)
∴y±3=±x/2
(複合同順)
前
>>36訂正。
y±3=±(1/2)x
(複号同順)
>>36 君ちょっと 病院行った方がいいと思うよ?
なんかの代謝性疾患かもしれないし
前
>>37 代謝は正常だ。
代謝が活発になるのは数学があるからだ。俺のせいじゃない。
糖質をじゅうぶん短時間に大量に脳内で消費する行為である数学は、当然多尿頻便の傾向をうながす。
一日四食とかふつうにあるし、尿の回数だって冬場はとくに二十四回でおさまるわけがない。
因数分解で
x*2-(y+5)x-(y-2)(2y+3)
まできたのですが、これからどうすればいいのかわかりません
教えていただけますでしょうか。
ちなみに、x*2∓(a∓b)x∓abにするのはわかるのですが、
やり方がわからなくて・・・すみません
ほとんど終わってるじゃん
x*2-(y+5)x-(y-2)(2y+3)
-(2y+3)と(y-2)の和が-(y+5)になるから
(x-(2y+3)) (x+(y-2))
ところでxの二乗はx^2で、x*2はx掛ける2だぞ
>>42 ab = -(y-2)(2y+3) なんだから,
aとbを-y+2と2y+3にするか, y-2と-2y-3にするかくらいしか選択肢がないだろう
両方試せば多分どちらか片方は当たる
...本当は1と-2y^2+y+6とかも考えなくてはならないが
ありがとうございます!
ただ、x*2-(y+5)x-(y-2)(2y+3) から
(x-(2y+3)) (x+(y-2)) にするときの組み合わせ方や符号がこんがらがります
適当にやってみてうまくいかなかったら別なのやりゃいいだろ。普通の因数分解と同じで何回もやってりゃそのうち直ぐに出来るようになる。
x+y+z=4の時 x^2 +y^2 +z^2 の取りうる範囲を求めよ。
これってシュワルツ不等式使う方法以外で解けるの?
1文字文字消去すりゃいいだけじゃん 典型問題だよ
全て正とかの縛りがなきゃ 割とeasyな問題
前
>>40 >>42 x^2-(y+5)x-(y-2)(2y+3)={x+(y-2)}{x-(2y+3)}
=(x+y-2)(x-2y-3)
xが重解をもつとき、
x=-(y-2)=2y+3より、
3y=-1
y=-1/3
x=7/3
2次方程式 x^2+x+1=0の2つの解をα、βおし
xの3次式f(x)=ax^3+bx^2+cx+d が
f(-1)=1, f(1)=1, f(α)=α, f(β)=βを満たすときの
a,b,c,dの値を求める問題の、解説についての質問です。
f(x)=ax^3+bx^2+cx+dにより、f(x)-xの3次の係数はaであるから②,③よりf(x)-x=a(x^3-1)である
↑これを分かりやすく説明してくれませんか
②・・・f(x)-xは (x-1)(x-α)(x-β)で割り切れる
③・・・ (x-1)(x-α)(x-β)=x^3-1
>>53 f(1)=1, f(α)=α, f(β)=βであるから、1、α、βはf(x)=xつまりf(x)-x=0の解
従ってf(x)-x=0は(x-1)、(x-α)、(x-β)を因数に持つ
f(x)は3次式で3次の係数がaであるのでf(x)=a(x-1)(x-α)(x-β)
最初の条件から(x-α)(x-β)=x^2+x+1であるからa(x-1)(x-α)(x-β)=a(x-1)(x^2+x+1)=a(x^3-1)
どの部分がわからないのかよくわからないけど
f(x)=a(x-1)(x-α)(x-β)
↑これのロジックを知りたいです。
なぜ係数がaが出てくるのかが分かりません
>>55 ax^3+bx^2+cx+dの3次の係数がaだからだよ
>>56 それは分かっているのですが、なぜそう考えられるのかを知りたいのです
>>57 どう説明すればいいのかなあ
例えばax+bがx+1を因数に持っていたらax+b=a(x+1)になるとわからない?
>>55 間違えてました
f(x)-x=a(x-1)(x-α)(x-β)
こうですね。f(x)からxを引くことをわすれていました
>>57 これならどうだろう
(x-1)(x-α)(x-β)を因数に持つ3次式はt(x-1)(x-α)(x-β)と表せるでしょう?
これを展開すると3次の係数はtでしょ?
上の問題では3次の係数はaなのでt=a
最高次数の係数を合わせれば良いということですね
ax+bがx+1を因数に持つならばax+b=a(x+1)
↑これが分かりやすかったです。ありがとうございます。
この手の奴は自分で式展開してみたりしないから分からんのだよなぁ
頭悪い癖に手間惜しむ
> 最高次数の係数を合わせれば良いということですね
理解しているかどうか不安が残るな
m*9,8*19,6+1/2*m*9,8^2=m*9.8*h
でのhを求めよ。
答えは24,5ですがやり方がわかりません
>>65 m≠0の場合、両辺をm*9.8で割る
m=0の場合、hは不定
前
>>52 m*9,8*19,6+1/2*m*9,8^2=m*9.8*h
m9.8で辺々割ると、
19.6+(1/2)9.8=h
h=19.6+4.9=24.5
あってる。
二次曲線の標準形ってなんですか?
これを使って証明出来たら証明できたってことにしてやるよってものですか?
例えば楕円だと円や線分のように標準形って特殊な場合をカバーできていないのですが、
なぜ標準形で証明出来たらすべての楕円で証明できたってことになるんでしょう?
二焦点が一致したとき、楕円は円になりますよね?
また二焦点からの距離の輪が二焦点間の距離と一致したとき、線分になりますよね?
楕円の定義は二焦点が一致することや二焦点間の距離と長軸の距離が一致することを否定する記述ってないはずですが。
楕円と円はまだしも、線分を楕円と呼ぶ人はいませんね
標準形を用いる場合、標準形で表せないものは除外して考えているんじゃないのか?
標準形で円をカバー出来ていないのなら、その場合は円は楕円ではないとして議論しているんだろう
>>68 それを使って2次曲線の分類が済んだので、ま、あとは用はない。。
直線は双曲線が退化したものだという解説がついているものもあるな。
x+2/x+1+x+7/x+6=x+3/x+2+x+6/x+5
この分数方程式の解き方が全くわからないです
通分して解いても答えがx=1になって代入しても等しくならないのでお手上げ状態です
1/x+3は(1/x)+3であって1/(x+3)では無い。
こういう曖昧な表記をする奴は 日頃からそういう事を全く気にしていなくて、正しく数式を認識をしてないんだよなぁ
ごめんなさい
この問題です

答え合わせならwolfram先生の方がたよりになるよ。
https://www.wolframalpha.com/input/?i=(x%2B2)%2F(x%2B1)%2B(x%2B7)%2F(x%2B6)%3D(x%2B3)%2F(x%2B2)%2B(x%2B6)%2F(x%2B5)
>>78 >x+2/x+1+x+7/x+6=x+3/x+2+x+6/x+5
(x+2)/(x+1)+(x+7)/(x+6)=(x+3)/(x+2)+(x+6)/(x+5)
だな
1+1/(x+1)+1+1/(x+6)=1+1/(x+2)+1+1/(x+5)
1/(x+1)+1/(x+6)=1/(x+2)+1/(x+5)
1/(x+1)-1/(x+2)=1/(x+5)-1/(x+6)
1/[(x+1)(x+2)]=1/[(x+5)(x+6)]
(x+1)(x+2)=(x+5)(x+6)
x^2+3x+2=x^2+11x+30
8x=-28
x=-7/2
前
>>67 >>80仮分数を帯分数にして辺々2を引くと、
1/(x+1)+1/(x+6)=1/(x+2)+1/(x+5)
通分すると、
(2x+7)/(x+1)(x+6)=(2x+7)/(x+2)(x+5)
2x+7≠0と仮定すると、
(x+1)(x+6)=(x+2)(x+5)
7x+6=7x+10
(6は10じゃねえ!!)
∴矛盾。
よって2x+7=0
x=-7/2
青チャート数2の、展開式の項の係数を求めるところをやっているんですが
一般項書かなくても簡単にできますね
質問を忘れていました。
のちのち一般項を書かないと解答が難しい問題が出るのでしょうか?
一般項を「わざわざ書けるように覚えないといけないですか?」って意味で書かないといけないか?って聞いてるなら 全然分かってないのかっていう感じだけど
解答作成時に一々一般形で見せてやる必要ありますか?っていってるのなら別に見せなくてもいいんじゃ無いって感じ
ただ過不足なくあげた感を出すには一般形書く必要あると思うけどね
わざわざ書けるように覚える。という意味をよく理解できませんが
数Aで習ったことをするだけですよね
今まで律儀に一般項を書いてrを求めていたので時間の無駄だったのかなと思い質問をしました。
こういうやつって授業きいてないの?
教科書の例題も読んでないの?
バカなの?
なんでわざわざ婉曲な表現するんですか?
それと何が言いたいの分からず、ただイキっているようにしか見えませんよ。
>>80 の問題に対していきなりx=-7/2
って答え書いてあったらどう思うのか?って話と同じじゃないの?
一般項を書くという事は(そう見えなかったとしても)全部展開して 該当箇所の係数を答えたって形になるけども
適当にちょこっと係数の計算部分だけ書いてあったら
記述解答としては見栄えは悪いよな。
2次方程式の解の公式を覚えないとのちのち困るような問題がでますか?ってのと一緒
解答の途中で2次方程式はアホほど出てくるし、その都度会の公式使わずに平方完成したり
して解いてたらむだに時間かかる
一般項を使う場面は解の公式ほど多くはないが、使わないと説明不足だったり、式が冗長になったりして
解答としては時間がかかる上にかっこ悪い
そもそも答えを出すのであれば全部脳内で処理すればいいので答えだけ書けばよい
テストというのは、答えにたどりつくまでのプロセスが正しいのかもテストしているの
だから、自分はこういう方法で解きましたよ、ってことを相手に伝えないといけない
大学入試レベルの数列について、
それが漸化式で与えられることと一般項として表わされることとが同値であることが解っていなければ
多分、解答のどこかに減点される記述が現れることだろうね。
デマこくでねえ
方程式に解けないものがあるように
数列の漸化式にも解のないものがあります
例:a(n+1)=1/a(n), a(0)=0
あ、「大学入試レベル」を付けたからという
言い訳は不要です
「同値」という数学用語を使う限りにおいて
主観を含む言葉の使用は許されません
728 オリーブ香る名無しさん sage 2019/02/16(土) 03:06:37.92 ID:hv4yFNTt
煽りの一言を付け加えないと気がすまない人って
最初から自分が感情論ぶつける人間ですって言ってるようなもんだよね
陰関数を偏微分したら何を表しますか
よくある崩落線を媒介変数の偏微分で解く問題の数覚的イメージが全然湧かないです。
高次元に埋め込んで意味を考えるにですが数式で導けても数覚が納得しない
例えばy=2tx--t^2などです
>>95 漸化式として成立しない例を持ち出されてもね。
また、一般項が解析的に得られるかどうかは問題にしていない。
崩落線てのは面白いな
グラフ全体が動くと思えばいいんじゃない?
何となく自己解決しました接線群と接平面群の動きが脳内でアニメーションしました
【イラクの伊藤詩織】 ナディア・ムラド(26)がノーベル平和賞、自民党とISは、米軍傀儡のレイプ集団
http://2chb.net/r/liveplus/1550283084/l50 100リットルの水が入る空の水槽に
水槽いっぱいになるまで毎分2リットルの水をいれていく
午後17:00には水が水槽の半分まではいっていた
この時点を基準にして、x分後に水槽の中の水の量がyリットル増えるとする
このときyをxの式であらわすと
y=2x+50
じゃないのか?
なんでy=2xやねん
17:00の時点の半分を基準にするんちゃうんかワレ
>>104 50入った時点を基準にしてそこから増える量をyとしてるからすでにその時点で入っている50は関係ない
国語の問題
>>105 まて、まて、じゃあこの時点を基準にしてとかいらんやんけ
そもそも午後17:00には水が水槽の半分まではいっていたがいらんやんけ
というか、50は関係ないとどうしていえる
そら五時の時点を基準とするから五時の時点でどんだけ入ってたって増えた量には関係無いわな
~時に半分まで入っていた。この時点(半分まで入っていた)を基準にして
じゃねえのかよ
言ってる意味がわかったわ。
これは発達障害の俺には理解しづらいわ。
つまり半分のとこからの基準、半分からの開始でってことか
国語マジック大嫌いだわ
いや違うよ
>この時点を基準にして、x分後に水槽の中の水の量がyリットル増えるとする
この時点 (五時丁度)を基準にしてx分後yリットル増える
五時1分なら2リットル増えているから
y=2xになるのは当然
5時を基準に52リットル増えてるわけじゃねぇからな
変化の割合=(yの増加量)/(xの増加量)にあてはめると
2=y/x だからy=2x
>>104 自分回答するがこの国語マジック問題はえぐいな
半分の50Lを0つまり基準としての関数になる
問題が
水の量がyリットル増えるとする
ではなくて
水の量がyリットルになったとする
であればy=2x+50
こんなんふつうに問題演習してれば見抜ける話
唐突にこの1問だけやったから見抜けなかったのがバレバレ
>>109 それ言わせてもらうけど小学生ではでないわ。
いや、小学生で比例は扱うけれどこのようなひねったのはない。
ちなみに俺が出したのは中学からの問題から。1次関数の問題。
つまり小学生からやり直せというのは無理があるね、
難関だとこのようなひねった出され方をするだろうけど。
基準の時点で水槽に入っている水の量=50(リットル)
基準の時点からx分経過後までに増える量=2x(リットル)
基準の時点からx分経過後に入っている量=2x+50(リットル)
>>116 まだ理解できてないね
そこらへん歩いてる中2に負けるレベル
「水がどれだけ増えたか」と「水が増えて結果的にどれだけになったか」の
違いを読み取れないということは日本人ではないのかもしれない
>>118 でもこのスレがあるおかげでワイに英知をあたえることになるんやで
>>118 >>114 100リットルの水が入る空の水槽に
水槽いっぱいになるまで毎分2リットルの水をいれていく
午後17:00には水が水槽の半分まではいっていた
この時点を基準にして、x分後に水槽の中の水の量がyリットルになったとする
このときyをxの式であらわすと
なったとするのした場合、適当なスレで問題マルチしてききまくったら
y=2x+50
になるわ
言葉のいいまわしってことだわな
>>115 >>119 >「水がどれだけ増えたか」と「水が増えて結果的にどれだけになったか」の
>違いを読み取れないということは日本人ではないのかもしれない
に書いてある通り 日本語の違い
君は1時30分と1時間30分の違いが分からない小学生と同じレベル
絶対的な量と変化量のどちらについて話しているのか日本語から読み取れていない
>>124 ううーーーーーんまぁ発達障害やからなあ
しゃーないぶぶんあるわ
>>124 1時30分は相対的な量?変化量?
1時間30分は変化量か
>この時点を基準にして、x分後に水槽の中の水の量がyリットルになったとする
最終的な量をきいてるから y=2x+50
>この時点を基準にして、x分後に水槽の中の水の量がyリットル増えるとする
基準からの増え方をきいてるから y=2x
俺の中でこう見解をだした
なおこの問題はマルチしまくって、多数の回答をきいてます。
公立中学学年3位以内→公立高校15位以内→大学
http://2chb.net/r/news4vip/1550315296/ まとめ
メンタルヘルス板での見解
>最初のが「水槽の中の水の量」(増えた分+すでに入っている分)
>2番目のが「増えた水の量」(増えた分だけ)
VIPでの見解 あるスレ1
>問題文の定義しだいやろ
VIPでの見解 あるスレ2
>17:00までに入ってる水のカウントの有無
>>129 戯れに、どんどん機械的な計算を追求してみよう。
sinθ=2 ならば、まず、sin^2+cos^2=1を満たしていなければならないので cos^2(θ)=-3。
よって、cosθ=√(-3)=i√3。
これより e^(iθ)=cosθ+i*sinθ=i√3+i*2=i(2+√3)。
この両辺の対数をとることにより iθ=log(i)+log(2+√3)。
よって θ=-i*(log(i)+log(2+√3))
>>124 よーくみると絶対的な量と変化量って書いてあるのか
絶対的なを相対的なで見間違えた
こういう部分
たとえば不定積分の計算してるときに最後の足し算で間違えるとかそういうミス
文章題でいうと日本語の読み違えとかいうミス
これをなんとかせねば
-1<=x<=1を満たす全てのxに対して、二次関数y=x2-2ax+a+2の値が常に正となるとき
aの値の範囲を求めよ
平方完成して頂点の式は出せたのですが、その後の検証の仕方がわかりません
質問失礼します。
スレチでしたらその旨お伝えください。
問題文の抜粋です。
「P市からQ町までは一本道で通じている。AはP市を出発し一定の速度でQ町に向かい、Aが出発した1時間後にBがQ町を出発してP市に向かった。2人が出会ったあと、3時間後にBがP市に、4時間後にAがQ町に到着した。…」
わからないので答えを見ているのですが、解説文には、「BはAより1時間後に出発してAより1時間早く到着していることから、2人が出会ったのはP市とQ町の中間点である。」と書かれています。
私はなぜ2人が出会ったのがP市とQ町の中間点になるのか理屈がわかりません。
どなたか論理的な説明をお願いします。
スレチよりマルチが嫌われるだろうな。
長方形で絵を描いてみる。
横軸は経過時間、縦軸は進行距離としてAの進んだ距離を時間の関数としてグラフを描き、
Aの軌跡が長方形の対角線となるように描き、そこにBの軌跡を追加する。
>>137 ダイヤグラムを書くとそうなる
縦軸をPからの距離 横軸を時間としてグラフかいたらいい
言葉で説明するなら
一時間の差を埋めるのに必要な距離と
一時間の差を作るのに必要な距離は同じと考えたらどうだろう
整数から成る非空な集合 A であって「a, b ∊ A ならば 3a - 2b ∊ A」をみたすものをすべて求めて
>>138 >>139 お二方、説明ありがとうございます。
ダイヤグラムという考え方が初耳でしたので、調べながら自分で考えてみたところ、理解出来ました!とても嬉しいです。
ダイヤグラムを使えば、平行四辺形が出来上がって対角線が中点で交わるというところから2人が出会ったのは中間点なのだと理解することができました!
本当にありがとうございました。( . .)
>>137 水槽の水の量の俺がきたぞ。
今後このスレにすむことになったんでよろしくな
それはいわゆる出会い算だな。
>>137 昨晩水槽問題で悶絶してた俺が
数学板にしばらくすむことになったので
解説した図をおいておくぞ
一応は数検1級保持者だ、負けられない戦いがここにある。

愛国者の愛がここにある
>>141 気にすることはないぞ。
スレチだろうがマルチだろうが
自分の思うようにすることで世界は変わる。
専用スレを立ててきこうがマルチしてききまくろうがそれは君の自由だぜ
なおマルチするにはコツがあって専用板のここにまず1つ、次にVIPのようなとこに1つもうひとつはなんJのような場所などを1つ、受サロや無関係そうなインテリそうなやつらがいるところに1つ、メンヘラ関係のとこに1つと10マルチくらいはして情報を集めるのがいいぞ。
前
>>84水槽の問題はなにも気にならなかったけど、
>>137なぜBが一定の速度で走れたかが理解できない。そんなことどこにも書いたらへんで?
Aが一定の速度、時速V㎞/時で走ったとすると、
P市とQ町の距離は、
V(㎞/時)×5(時間)=5V(㎞)
AがBと出会ってからQ町に着くまでに走った距離は、
P市からAがBと出会った地点までの距離をx(㎞)として、
V(㎞/時)×4(時間)=5V-x(㎞)
これを簡単にすると、
x=V(㎞)
これはP市とQ町の距離の1/5にあたる。
すなわちAがBと出会った地点はA市とQ町の中間地点じゃなく、はるか手前。
Aの行く人生の道のりは、Bと別れてからのほうが5倍ぐらい長いってことじゃないか? 減速すれば知らんが。
逆にBがAと別れたあと減速したんじゃないの? それか転けたか。
>>137 よく考えるとBは一定速度であることはかかれていないな
だが結果的に1時間ずれで出発して、1時間ずれでついたわけだ
そこで見分けるしかなかろう
もしかすると問題文にはBも一定の速度でと書いてあったのかもしれない
知る由あない
>>143 やっぱ水槽ニキ日本語弱すぎちゃう?
問題文読めてないよその図じゃ
>>141 解決したならマルチしたところを閉じてこいよ
友人から出された問題が解けなくて困ってる
正の実数a,bがa+ab+b=1を満たすとき、(a^2 +1)(b^2 ;1)のとりうる範囲を求めよ
全く分からんので分かる人教えてくれ
>>143 >>137です。
解説して頂きありがとうございます!
こちらの図は、
>>138さんと
>>139さんに教えていただいたダイヤグラムの考え方ですね!自分で書いたものよりわかりやすく理解出来ました。わざわざありがとうございます。
数検一級すごいですね!
>>144 >>137です。
恥ずかしながらマルチという言葉の意味がわかっておらず、知らずに複数の掲示板に書き込んでしまいました。大変失礼致しました。
お心遣いありがとうございます。
以後気を付けます。
>>146 >>137です。
私が聞きたかったことは何故ABが出会った地点がPQ間の中間点なのかということでしたので、関係のない所を省略してあります。
問題文は、
>>137の「」内の後にこう続きます。
「…AがQ町に到着した。Bの歩く速度がAより毎時1km速いとすると、P市とQ町の間の距離は何kmか。」
しかしながら、Bも一定の速度であると書き足しておくべきでした。大変失礼しました。
>>154 a+ab+b=1 の両辺に1を加えて変形すると
1+a+b+ab=2
(1+a)(1+b)=2
a, b は正の実数より 0<a<1, 0<b<1
あとは b=(1-a)/(1+a) を代入して
a だけの式にしてから
最大、最小を求めればよい
解は 24-16√2 ≦ 与式 < 2
最小値は a=b=-1+√2 のとき
前>>147
>>157なんだ歩きか。てっきりバイクかチャリだと。
遅いA ちょっと速いB
↓↓↓ ↓↓↓
~彡∩∩はや! ∩∩
彡((`o`) (`) )
彡(っ┳υ (_υ_)
◎゙υ┻◎゙_/_◎゙┻◎゙
キコキコ……/_/ゴロゴロ……
_/_/_/_/_/_/_/
(解きなおし)Aの速度が時速V(㎞/時)で、Bの速度が時速V+1(㎞/時)とすると、P市とQ町の距離は、
V(㎞/時)×5(時間)=5V(㎞)――①
V+1(㎞/時)×3(時間)=5V(㎞)――②
AがBと出会ってからQ町に着くまでに走った距離は、P市からAがBと出会った地点までの距離をx(㎞)として、
V(㎞/時)×4(時間)=5V-x(㎞)
これを簡単にすると、
x=V(㎞) ――③
(ちなみにこれはP市とQ町の距離の1/5にあたるP市寄りの地点)
②より、3(V+1)=5
3V+3=5
3V=2
V=2/3(㎞/時)
Vの値を①または②に代入し、P市とQ町の距離は、
5V=10/3(㎞)
(ちなみにAとBの出会いの場所は、③よりx=V=2/3 すなわちP市からQ町に向かって2/3㎞の地点) 前
>>160考え中。
Bが出発してからAと出会うまでの時間をt(時間)とすると、
(V+1)t=5V-x――④
BがAと出会ってからP市に着くまでの時間は、
AがBとすれちがってからQ町に着くまでの時間より一時間短いから、
x÷(V+1)+1=(5V-x)/V――⑤
④を⑤に代入すると、
x÷(V+1)+1=(V+1)t/V
③x=Vより、
{V/(V+1)}+1=(V+1)t/V
t=V[{V/(V+1)}+1]/(V+1)
=V(2V+1)/(V+1)^2
④にtの値とxの値を代入すると、
(V+1)V(2V+1)/(V+1)^2=5V-V
V(2V+1)/(V+1)=5V-V=4V
2V^2+V=4V(V+1)
2V^2+3V=0
V=0または-3/2
Aは停まっているか、
時速1.5(㎞/時)で逆走。
>>146 5時間ってのはどこから出て来た時間なんだい?
>>161 >>137です。
この問題は、AB2人が出会ったのがPQ間の中間点であるとわかればすぐに解けました!
PQ間の距離をxとすると、
Aの速さはx/8(時間)
Bの速さはx/6(時間)
Bの方が毎時1km速いことから、この2つの速さの差が1km、つまり
x/6-x/8=1
こちらを解いて、x=24となり、PQ間が24kmと答えが得られます。
考えて下さりありがとうございます!
>>150 お手本っていうかさ
>2人が出会ったあと、3時間後にBがP市に、4時間後にAがQ町に到着した。
の解釈が間違ってんのだよ
あの図ではAもBも P から出発していることになるしね。
前
>>161やりなおした。
>>137これたぶん正解。
↓ ↓ ↓
Aの速度を時速V(㎞/時)とすると、Bの速度は、
時速V+1(㎞/時)
P市からAとBが出会った地点までの距離をx(㎞)、
AとBが出会った地点からQ町までの距離をy(㎞)とすると、
AとBが出会ってからBがP市に着くまでの距離x(㎞)は速さ(V+1)×時間(3)で表され、
x=(V+1)×3――①
AとBが出会ってからAがQ町に着くまでの距離y(㎞)は速さ(V)×時間(4)で表され、
y=V×4――②
AがP市を出発してからBに出会うまでの時間は、
距離(x)÷速さ(V)で表され、
BがQ町を出発してからAと出会うまでの時間は、
距離(y)÷速さ(V+1)で表され、
前者は後者より1時間長いから、
x/V=y/(V+1)+1――③
求めるP市とQ町の距離は、
①、②より、
x+y=3(V+1)+4V=7V+3(㎞)
①、②を③に代入すると、
(3V+3)/V=4V/(V+1)+1
(3V+3)(V+1)=4V^2+V(V+1)
3(V^2+2V+1)=5V^2+V
2V^2-5V-3=0
(V-3)(2V+1)=0
V>0だから、
V=3(㎞/時)
∴x+y=7・3+3=24(㎞)
>>132 θ=π/2+2nπ ±i*log(2+√3)
cosθの候補がもう一つあるのをお忘れなく。
>>163 今さらだけどダイアグラムを知らなくても似たような考え方で出会ったのが中間点だということはわかるよ
BがスタートしたときにAがいる位置をR、BがゴールしたときにAがいる位置をSとすると、PRもSQもAが1時間かけて進む距離だから同じ
従ってRSの中点はPQの中点と一致する
BがQをスタートしてPに到達するまでの間にAはRからSに進んでいるわけだが途中はどうなっているのか考えると
Aが中間点に到達する前はBも中間点に到達せず、Aが中間点に到達したときBも中間点に到達、Aが中間点を超えたらBも中間点を越えている
つまり、出会うのは中間点
イキるのはいいが
>>164-165あたりを見てもう一度考えたらどうだ?
>>170 同じ距離を互いに端からすすむのだからその図で問題なかろう
反論はよ
計算問題で「そこ、符号の+と-が違ってるよ」って注意したら
「数字が合ってるから問題ない、反論はよ」って返す奴か
厄介だな
というか水槽ニキの設定なら 誰も悩まずにダイヤグラムなんて書くことなく処理できるんだよなぁ
【池江の白血病、科学的見解】 飛行機での移動で宇宙からの放射線を浴びたせい、福島原発ではなく
http://2chb.net/r/liveplus/1550460074/l50 階級値に関わる質問です。
身長で150以上155未満(cm)の時は階級値は152.5(cm)なのはわかるのですが、たとえば参加人数のように整数値で10人以上15人未満のとき、階級値は10~15の中央値で、12.5となるのでしょうか。それとも10人以上15人未満なので10,11,12,13,14の中央値で12となるのでしょうか?
前
>>166 >>168数学的に数式と数値で示せると思う。
①より、
x=3V+3=3・3+3=12(㎞)
②より、
y=4V=4・3=12(㎞)
∴x=y
よってAとBはP市とQ町の中間点で出会う。
a^3+b^3+c^3-3abcの因数分解について質問です。
結果はもちろん、一般的な作り方も理解しています。
ただ、どこかで解と係数の関係をうまく使って作り出しているのを見たことがあって、それがどのようなものだったかどうしても思い出せません。
どのようなものかご存知の方いらっしゃいませんか?
a^3+b^3+c^3-abc 解と係数の関係
でググレカス
a^3+b^3+c^3-3abc = (a+p)(a+q)(a+r) とすると、
p+q+r=0, pq+qr+rp=-3bc, pqr=b^3+c^3=(b+c)(b^2-bc+c^2) … ①
ω=exp(2πi/3)として、p=b+c, q=ωb+(ω^2)c, r=(ω^2)b+ωc が ①を満たす
よって与式 = (a+b+c)(a+ωb+(ω^2)c)(a+(ω^2)b+ωc) = (a+b+c)(a^2+b^2+c^2-bc-ca-ab)
前
>>178 >>179 a^3+b^3+c^3+3abc
=(a+b+c)^3-3(a^2・b+a^2・c+b^2・c+b^2・a+c^2・a+c^2・b-6abc+3abc
(^ω^)
>>137 です。
数日経ってまたここを覗きに来ましたが、私の出した問題について揉めている?ような雰囲気になっていて驚きました。皆さんのおかげで理解出来たので感謝しています。どうせggrksって言われて終わりだろうなと思っていたので。
高校生に恥をしのんで聞いてみてよかったです。
考えてくれてありがとうございました。
ですのでどうか、揉めるのはおやめください。
0<x<1において
2^x>x^2+1が成り立つ
これを文系の範囲で証明できませんか?(数Ⅲ微積は未履修です)
前
>>183 >>185 y=2^xのグラフと、
y=x^2+1のグラフを書いて、
0<x<1においてどっちがおっきいか調べたらわ?
あいだどんなけ刻めるかやね。
絶対値が4より大きく7以下の整数の個数という問題なんだけど、
これいくつになるの?6個?
>>186 あいだを何個かとって大体成り立つだろうという予想は立ててるんですが、証明ができなくて困ってます
数Ⅲやるしかないんでしょうか
どういう状況で質問してんの?
受験でこれに対応したいってなら微積やった方が圧倒的に早いでしょ
例え上手い方法を誰かに教えて貰ったからといって自分じゃ絶対気が付けないしなんの汎用性もないからな
>>185 あらすじを書くとこう
・f(x)=2^x-(x^2+1)とおく。f(x)は0<x<1で連続かつ(少なくとも)2回微分可能
・0<x<1でf''(x)<0、よって0<x<1でf'(x)は単調減少
・f'(0)>0,f'(1)<0、よって0<c<1かつf'(c)=0となるcがある
・f(0)=0かつ0<x≦cでf'(x)>0、よって0<x≦cのときf(x)>0
・f(1)=0かつc≦x<1でf'(x)<0、よってc≦x<1のときf(x)>0
・よって0<x<1のときf(x)>0
・よって0<x<1のとき2^x>x^2+1 □
文系で理解できるかどうかは努力しだいかな
>>192 春休みの自由研究の途中で出てきた不等式です
大学付属校なので受験はしないです
なので数Ⅲをやるつもりは今のところありません
所詮自由研究なので、この不等式が成り立つことを認めた上で論理展開しても構わないんですが、
数Ⅱまでの知識でも証明できるならしておきたい(知りたい)ってだけです
>>193 文系向けに噛み砕いてみる
数学的に厳密でないかもしれないけどご容赦。
・(左辺)>(右辺)を証明したいので、f(x)=(左辺)-(右辺)と置いてみる。0<x<1のときf(x)>0と言えれば元の命題が証明できる・f(x)のグラフを描いてみると、f(0)とf(1)がともに0であり、0<x<1ではf(x)がプラスであることがなんとなくわかる
・「0<x<1でf(x)がプラス」を証明するためにグラフの傾きを調べたいので、導関数f'(x)の様子を調べてみる
・f'(0)>0だから、x=0のところでf(x)は増加中、f'(1)<0だから、x=1のところでf(x)は減少中であることがわかる
・0<x<1のすべてでf(x)>0であると言うために、範囲の途中にf'(c)=0となるcがあって、0からcまではf(x)が増加、cから1まではf(x)が減少であることを示す
・そのために導関数f''(x)の様子を調べる
大学附属って文系でも数三までやらせられる所多いのに珍しいな。
経済とか商とか経営系でも四月頭からばしばし微積使うから純粋文学部以外は数三ぐらいは必須だからやるみたいな所の方が多いのに
>>189 >>190 やっぱり数学板って無能しかおらんのじゃないか?
絶対値の問題に詳しいひと 数学
http://2chb.net/r/news4vip/1550810571/ 公務員障害者採用試験スレ20【精神専用】
http://2chb.net/r/utu/1550803131/ なおここにもマルチで立てて質問してるが。
文系理系でもあまり出来や素質は違わないが、経験やカリキュラムの面で大きく差が出ているだけではないか?
>>197 これはニュー速で指摘されてる通りだね。
6個も、無限個も、日本語の解釈として有りうるのでどっちも正解になってしまう。
強いてどっちか一つ選ぶなら読点の存在から無限個の方を選ぶことになる。
指数関数の微分を数三だと扱わないってのと
ネイピア数を扱わないから自然対数取ることも出来ない
三次函数ぐらいの微積分なら文系もやる 笑
文系だと 2^x の微分ができないので増減表以前の問題。
2^xの凸性を認めてもらえるなら手はあるけどくだらない。
結局、数Ⅲまでやったらスパッととけて、数Ⅱまでだと無意味に難しい問題なんかそもそも意味ない。
文系・理系のカリキュラムも知らない馬鹿がなんでドヤ顔で講釈たれてるの?
「できません」→「この無能が」
「できます」→「なにそのドヤ顔」
これが数学板
無理ってことね。了解
>>193とか
>>195みたいな無能って何考えてんだろうな
誰の役にも立たない長文書いて
こっちは微積使うな(初等的に)ってオーダーしてんのに
無理なら無理っていえよ
バカには無理ってはっきり言ってあげた方が本人のためってことだ
a,bを整数の定数とし f(x)=x^2+ax+b とする。
任意の整数xに対してf(x)>0 であうことは、任意の実数xに対してf(x)>0 であるための( )
という問題で
答えは私は必要条件だと思ったのですが正答は必要十分条件らしいのです。
どうしてなんでしょうか。
数Ⅲやるつもりもない無能が教えてもらう人を無能扱いw
>>208 おそらく整数以外の部分でf(x)が0以下になる可能性がある
って考えて必要条件って思ったのだろうけど
a奇数で重解にするためにはbが整数に反するし
a^2-4bが整数である縛りから0<√D<1になり得ないから整数と整数の間だけx軸を切り取るみたいなのが無理
>>208 ちゃんと読んでいなかったすまん。
必要性は明らか。
十分性について、aが偶数の時は、最小値を取るxは整数になるので成り立つ。
aが奇数の時、xが整数ならば整数の掛け算なのでf(x)も整数。
よって、1/4-D/4≧1
∴D≦-3
>>208 >>211,212 さんの回答からわかる通り、これ、瞬間で答えるには結構難問だね。
問題文中の >0 が ≧0なら「必要条件」が正解になるところが面白い。
d^2yってグラフ的に何ですか
dxの2次関数と見なせますか?
211様212様ありがとうぞざいます。十分条件もいけるのですね。
それにしても入試でこの形式だと普通は必要条件のみ答えてしまうのではないですか。
ちょっと意地悪なカンジがすます。
Fラン文系用ならともかく、もし正解が必要条件なら何でもサル問題すぎて怪しいと疑わないか?
文系レベルのアホがゴミカス問題をいつまでも難しい難しいって騒いでて邪魔
>>219 おまえが211や212でなければそんなことを言う資格はなし
こういう奴に限って全然質問に答えられないんだよなw
そもそもなんの根拠もなく
「整数で常に正でも整数じゃないところじゃ負になるかもしれないんだから成り立たない!」
ってバカ丸出し。
そういうバカを振るい落とすために問題は作成されている。バカは一生苦しんどけ
馬鹿が発狂していてワロタ
この馬鹿が何か質問に答えられるかどうかが見ものだなw
>それにしても入試でこの形式だと普通は必要条件のみ答えてしまうのではないですか。
>ちょっと意地悪なカンジがすます。
何言ってんだコイツw
こいつ進研模試で50点も取れないアホなんだろうなwww
>>224 ある無矛盾な公理系τの任意のモデルに対してある論理式φが常に真となるならば、τからφがLKにおいて証明可能となることを示せ
>>978 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 00:59:28.70 ID:BoJlALsC [1/20]
>>977 >より進んだ数学の中には、多項式としては 0 ではないが、それを多項式関数と見た場合は 0 というようなものがある。
ありません
複素関数を考えるにしても、多項式、すなわち連結領域上の正則関数を考えるならば、一致の定理よりある部分で0なら全体で0です
多項式とは有限次元で打ち切りですから、収束半径は無限大、すなわち複素数全体で0となります
前スレ
>>979 自分:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:11:11.10 ID:MxKVVcoK [2/4]
>>978 標数2の素体上で多項式関数 x^2+x を考えると、これは常に0関数となります。
前スレ
>>980 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:13:16.71 ID:BoJlALsC [2/20]
>>979 殺す
代数の知識がかけらもないアホwwwwwワロスwwwwwww
ふつーに標数>0の話してるってわかるよなあ?
それを複素関数ってwwww
数学科すら出ていないウンコ丸出しでワロタ
ふっふっふっふっふくそかんすううううう?????wwwwwwwwwwww
長さxが与えられたとき、
x^2の長さの線分を作図するにはどうすれば
x=1ならそのまんま
x>1なら高さが1で面積がx^2の平行四辺形を作れば長辺の長さがx^2になる
x<1なら長辺が1で面積がx^2の平行四辺形を作れば短辺の長さがx^2になる
描き方は説明が面倒なので省略
こんなのしか思い浮かばなかった
>>235 相似を利用する
1:x=x:A
よって、A=x^2
こんなの教科書にのってるじゃん
236とか237とかは教科書も持ってないアホなおっさん
一点x=aのみで定義されている関数は
x=aで連続ですか
物のつながりを表す数学的構造のことです
連続性とは、そのような位相構造に基づき定義されます
↑これが数学板の実力です↑
専門板なのに異常にレベルが低い
せいぜい数学の少しできる高校生レベル
【超悪質!盗聴盗撮・つきまとい嫌がらせ犯罪者の実名と住所を公開】
①井口・千明(東京都葛飾区青戸6-23-16)
※盗聴盗撮・嫌がらせつきまとい犯罪者のリーダー的存在/犯罪組織の一員で様々な犯罪行為に手を染めている
低学歴で醜いほどの学歴コンプレックスの塊/超変態で食糞愛好家である/醜悪で不気味な顔つきが特徴的である
②宇野壽倫(東京都葛飾区青戸6-23-21ハイツニュー青戸202)
※色黒で醜く太っている醜悪黒豚宇野壽倫/低学歴で人間性が醜いだけでなく今後の人生でもう二度と女とセックスをすることができないほど容姿が醜悪である
③色川高志(東京都葛飾区青戸6-23-21ハイツニュー青戸103)
※色川高志はyoutubeの視聴回数を勝手に短時間に何百何千時には何万回と増やしたり高評価・低評価の数字を一人でいくつも増やしたり減らしたりなどの
youtubeの正常な運営を脅かし信頼性を損なわせるような犯罪的業務妨害行為を行っています
※色川高志は現在、生活保護を不正に受給している犯罪者です/どんどん警察や役所に通報・密告してやってください
【通報先】
◎葛飾区福祉事務所(西生活課)
〒124-8555
東京都葛飾区立石5-13-1
℡03-3695-1111
④清水(東京都葛飾区青戸6-23-19)
※低学歴脱糞老女:清水婆婆 ☆☆低学歴脱糞老女・清水婆婆は高学歴家系を一方的に憎悪している☆☆
清水婆婆はコンプレックスの塊でとにかく底意地が悪い/醜悪な形相で嫌がらせを楽しんでいるまさに悪魔のような老婆である
⑤高添・沼田(東京都葛飾区青戸6-26-6)
※犯罪首謀者井口・千明の子分/いつも逆らえずに言いなりになっている金魚のフン/親子孫一族そろって低能
⑥高橋(東京都葛飾区青戸6-23-23)
※高橋母は夫婦の夜の営み亀甲縛り食い込み緊縛プレイの最中に高橋親父にどさくさに紛れて首を絞められて殺されそうになったことがある
⑦長木義明(東京都葛飾区青戸6-23-20) ※日曜日になると風俗店に行っている
閉区間で微分可能は考えないのですか
|x|は[0,∞]が定義域ならx=0でも微分可能ですか
サイコロをn回振って出た目を全て掛け合わせた数の期待値って
(一回振って出る目の期待値)^nで合ってますか?
質問です。
瀬山四郎先生のトポロジー柔らかい幾何学の本を読んでいます。
10ページめの
"S^3は中身のつまった2個の3次元球面体の表面を貼り合わせて作られことになりますが.."
これはx^2+y^2+(z-2)^2=r^2 の rを[0,2),[2,∞)に分けることらしいのですが
なんで当たり前のことをわざわざ言うのでしょうか
まだ射影幾何的なことは出ていません。
S^2のときは、いいのですが、S3では球面をボールの外と同一視しているということでしょうか?
正六角形の辺をサイコロが出た目だけ反時計回りに回る
3回振って出発点に初めて到着する確率はなんでしょうという問題で
自分は1回目で6以外が出ればいいから5/6
2回目で、出してはいけない目は1つ(出発点に到着してしまう目)だから5/6
3回目は到着しなければならないからどの点にいても1/6
5/6×5/6×1/6で25/216となりました
答えはあっているのですが、模範回答には場合分けによる解法のみで、こんな解答は載っていませんでした
もしこの解答に抜け目があれば教えてください
教科書の樹形図の項目に問題があれば
全通りを図に書くのが正解となる
教科書・問題集の全体を晒さないと
判断できない
251に関連するんですが
サイコロをn回投げて出た目の総積が12で割り切れる回数の期待値
は
(4で割り切れる回数の期待値)*(3で割り切れる回数の期待値)
で合ってますか?
それは合ってないんじゃないか?
後者の方が大きくなるように思えるが
総積が2や3のような素因数で割り切れる回数の期待値ならすぐ求まるのですが...
2*3や2*2*3のように複数の素因数で割り切れる回数の期待値のときはどう求まるんでしょうか?
>>262 1/6×n以外での出し方考える事からはじめたら?
あーごめん1/6ではないか ただまぁいいたいのは一回辺りの期待値出してそれをn倍するみたいな方法でないってこと
確率について教えてください。
10000のクジの内、当たりが100枚の場合
当選確率は100/10000で、当選確率1%と表示されそうですが
実際にクジを購入する場合に1枚しか買わなかった場合
当選確率は1%になるのでしょうか?
このケースでは、100枚購入した場合の当選確率が1%だと思うのですが、どうでしょうか?
>>264 6と偶数
3と4
3と偶数2つ
で場合分けですかね?
ここから期待値を求める方法が分かりません
>>266 割り切れる回数をカウントしないといけないから
君のやり方だと12で割れるかどうかを考えるのには多少は役に立つけど
何回割れるかを考えるのには向いてないから
真面目にそれぞれ2,3,4,6が出る回数を考えて何回割れるか考察して それが何パターンあるかを考えるってのがいいと思うよ

違いを教えてください
30%、100個に30個、10個に3個は全て意味が違うのですか?
>>270 上はサンプルが大量にあって30%が不良品って分かってるケースで考えている
正確にはもし一個目に不良品を引いたら、二個目を引く時に全体の中から不良品が一個分少なくなっていてその分不良品を引く確率が下がってるはず。
しかし大量にあるなら大した影響は無いから無視できる。
下はサンプルがホントに100個しかなくて そのうち30個が不良品ってのが分かってるケース
でも不良品が30%と言われて全数が与えられていないなら通常は上で考える
なぜなら下で考えるにはサンプル数によって答えが変わるから
ここ話題がすぐ変わってつまらんな
単発スレ立てるは
二者択一の◯×問題の正解率がどの問題も等しく80%である時、
五者択一の正解率の求め方ってありますか?
例えば五者択一なのに、1問1問を二者択一で仮に回答を行ったところ、××◯×◯という回答をした時には「◯が2つは有り得ない、おかしい」という普通の判断を行うものとします
>>274 問題の前提がわからないのでこういう仮定をしてみる:
・正答を知っている回答者は必ず正答を選ぶ
正答を知っている回答者の正答率は1/1
・正答を知らない回答者は選択肢を無作為に選ぶ
正答を知らない回答者の正答率は二択卓なら1/2、五択なら1/5
・上記2通りのどちらか以外の回答者は居ない
回答者のうち正答を知らない割合をxとすると、
二択の場合の正答率は(1/1)(1-x)+(1/2)xで、
五択の場合の正答率は(1/1)(1-x)+(1/5)x
>>274 設定がよくわからない
どんな問題であろうと二者択一なら必ず8割正解出来る人物が存在するという仮定してその人物が五者択一問題をどれくらいの割合で正解出来るかってこと?
家庭に無理あるんでないんだろうか
>>275 >>276 申し訳ない
~~は◯か×か?という問いの正解率が80%の前提
次の5択の中に正解は1つ
a、~~は◯である
b、~~は×である
c、~~は◯である
d、~~は◯である
e、~~は×である
~~で省略しましたが全部違う問いです
この五択の正解率は導けるのかなと思っての質問でした
アンパンマンはパンである◯か×か
カレーパンマンはラーメンである◯か×か
食パンマンはそばである◯か×か
チーズは犬である◯か×か
ジャムおじさんはおばあさんである◯か×か
このような一問一答の正解率が80%の人がいて、この一問一答で構成された五者択一
a、アンパンマンはパンである
b、カレーパンマンはラーメンである
c、食パンマンはそばである
d、チーズは猫である
e、ジャムおじさんはおばあさんである
の正解率が導けるのかなと思っての質問です
この正解はaですが、仮にaとbの両方が正解だと思っても、両方は有り得ないだろう、という判断が前提となる話です
そんなの仮定出来るのかなあ?
二者択一を50万問やるとだいたい10万問間違える
正解は教えずに、間違えた10万問だけ別の問題に差し替えて再び50万問やらせたらどうなるんだ?
正解の選択肢をaと仮定しても構わない。解答にaを選ぶ可能性があるのは次の2パターンである。
i. 選択肢を読んでaを○と判断した場合
(1) 他の選択肢をすべて×と判断した場合: (4/5)^5
(2) 他の選択肢に1つだけ○と判断し、1/2の確率でaと解答した場合: (4/5)×4×(4/5)^3×(1/5)×(1/2)
(3) 他の選択肢に2つだけ○と判断し、1/3の確率でaと解答した場合: (4/5)×6×(4/5)^2×(1/5)^2×(1/3)
(4) 他の選択肢に3つだけ○と判断し、1/4の確率でaと解答した場合: (4/5)×4×(4/5)×(1/5)^3×(1/4)
(5) 他の選択肢もすべて○と判断し、1/5の確率でaと解答した場合:
(4/5)×(1/5)^4×(1/5)
ii. 選択肢を読んですべて×と判断し、1/5の確率でaと解答した場合: (1/5)×(4/5)^4×(1/5)
これらをすべて足すと8660/(5^6)=0.554…
複数を○と判断した場合にどうするのかは等確率で選ぶことにしちゃっていいんだろうか
>>280 正解率は常に80%としています
その場合、80%の前提を覆してしまうので想定していません
>>281 学がないので計算式はよく理解できませんが、55%というのには感覚的には納得できる数字です!
ありがとうございます!
よければこの55%を70%や80%にするために、元の一問一答の正解率がいくつになれば良いのか(例では80%としていた部分)も教えてもらえないでしょうか?
>>282 やはりそこの定義付けが必要になりますか
ひょっとしたらなくてもいけちゃうのかな?とも思ったのですが、必要でしたら等確率で構いません
最初に2つ○となった場合、そのうちのどちらかを選ぶのは二者択一なのだからその中に正解のaがあるなら80%でaを選ばないとおかしいことにならないか?
じゃあ、3つ○となった場合、その中にaがあったらどうするのかとかちょっと不確定な要素が多いように思う
>>284 あくまでフラットな状態での正解率が80%であって2つ◯がつく=わからない問題である、と捉えた方が実践的なのでわからない問題=等確率でOKです
>>285 それでは二択を8割で合わせれないよ
選択肢2つのケースはどう考えるんだ?
二択を8割で当てられるとしてそれが5問並んでいる
答えを一つが前提にすると5つとも正しいと判定した場合その5個の中からランダムに一つ選ぶ?
全部解なしと判断した時は五択にかける行動をするのか?
選択肢を二者択一で比較検討した時にベターなものを80%で選べて
ダメなもの同士を比較したときはふつうに1/2で選ぶ
特定の二択につき一回しか比較不可能
っていうルール下で
どういうセレクションが1番正答率高く出て何パーなのか
みたいなのなら考えれるのでは?
>>283 複数○が付いた場合の行動を
>>281のように定義して良いのであれば
各選択肢の○×を正しく判定する確率がxのとき、正しい選択肢を解答できる確率はx(2x^3+x^2+x+1)/5
あとはwolframとかで近似解計算してくれ
>>286 わからない=等確率
で良い、と判断したので
アンパンマンはパンである→2択を選ぶ→結果80%
アンパンマンはパンである
カレーパンマンはラーメンである
両方◯と判断した場合=わからない=等確率という仮定です
>>287 >>289 その通りです
五角形の鉛筆転がします
仮に4択までは絞れるなら1/4にしたいところですが
>>291 walframですか
ぐぐってみます
前提は◯2つ以上で等確率という計算ですよね
それで大丈夫です
ありがとうございました
二択なら8割正解出来る人が、○2つのときそこに正解があるとしても等確率って設定にどうも納得出来ないわ
全然実践的じゃないように思う
そもそもどんな問題でも二択なら正解率80%って設定が実践的じゃないけど
そういう設定をするならすでに答えを知っているが4/5で当たるくじを引いて当たりだったらそのまま正解を答え、外れたらわざと不正解するとかじゃないと実現出来ないんじゃないだろうか
でもその場合だと何択であろうと正解率80%になっちゃって面白くもなんともないけど
>>275の設定が現実的な感じがするね
xは0.4になる
1対1の演習を演習題も合わせて全て回答、理解した場合、進研模試の偏差値はどれくらいが期待できますか?
超えないですよ
満点とったことありますけど80ピッタリでしたから
80.0で本当にぴったりだったんで上限設定されてるのかと思ってました
データの分析を習ったことのないいい年こいたジジイなんだろ
高卒でもない限り偏差値なんて知ってるぞまだ中卒の小僧
偏差値の定義くらい知ってますけど
あなたたちと一緒にしないでください?
東大プレとか100越えたことあるけど、進研模試とか平均高すぎて80も取れない気がするんだけど
なんで上限設定なんてものがあると思ったのかが謎だけどな
数学で満点で80越えないなんてかなり珍しいんじゃないか?
他の回の1位がどんなだか見りゃわかることなんじゃ?
分布表とか出ないの?
>>307 そんなことないと思うけどなあ
進研模試って駿台とかと比べたら下の方まで受けるだろう?
それで満点で80以下が当然なら簡単すぎてマーチレベルくらいからもうほとんど差がつかなくなって模試の意味なくなっちゃうじゃん
実際そんなことにはなっていないようだよ
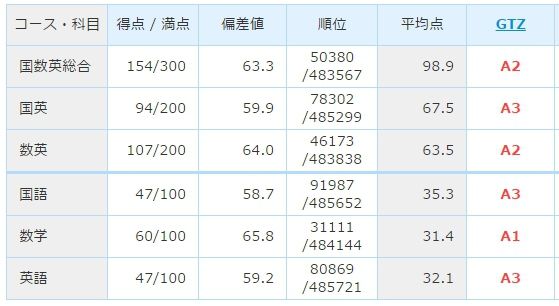
これだと数学満点なら偏差値88くらい
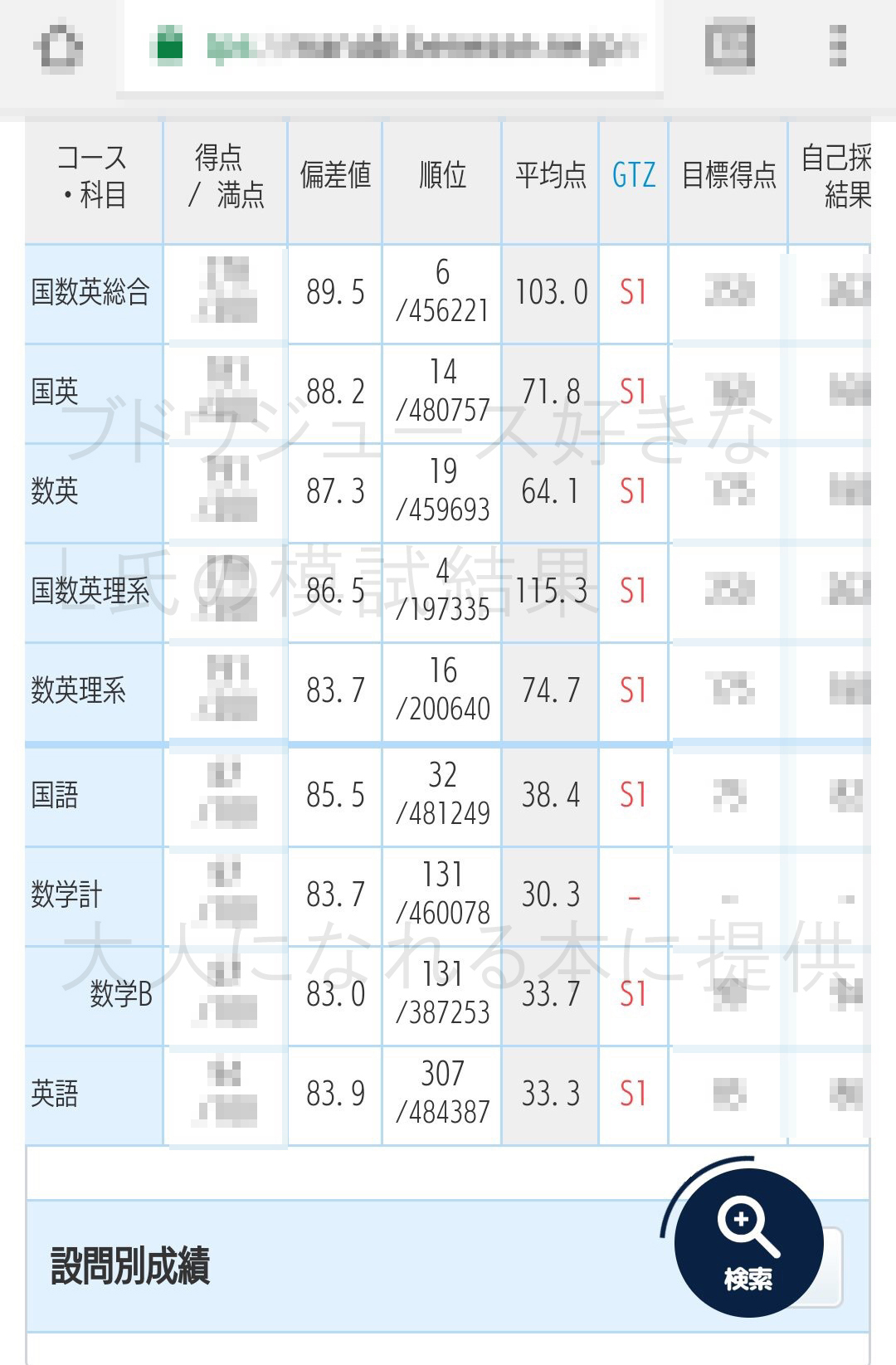
これなかは得点が無いから満点だったらどうだかわからないけど満点でなくても80越え
やっぱ進研模試でも満点で80.0は例外的に簡単だったんだと思う
進研模試の数学ってミスったらバカwwwwwみたいな感じだしな
だから偏差値の定義も頭に入ってないバカな爺なんだろ
それに進研模試が平均高すぎてと書いてるキチガイがいるけど
進研模試はバカ学校も受けるから平均点は3割程度。
調べる能力もない馬鹿はいちいち書き込まんでいい。
なにがバカかというとろくに調べる能力も労力もないウスラバカが
自分の狭いダサい価値観のみが普遍的な事実であるかのように妄想
してるところ。
まじで病院いってこい。
>>312 ある無矛盾な公理系τの任意のモデルに対してある論理式φが常に真となるならば、τからφがLKにおいて証明可能となることを示せ
>>313 >>978 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 00:59:28.70 ID:BoJlALsC [1/20]
>>977 >より進んだ数学の中には、多項式としては 0 ではないが、それを多項式関数と見た場合は 0 というようなものがある。
ありません
複素関数を考えるにしても、多項式、すなわち連結領域上の正則関数を考えるならば、一致の定理よりある部分で0なら全体で0です
多項式とは有限次元で打ち切りですから、収束半径は無限大、すなわち複素数全体で0となります
前スレ
>>979 自分:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:11:11.10 ID:MxKVVcoK [2/4]
>>978 標数2の素体上で多項式関数 x^2+x を考えると、これは常に0関数となります。
前スレ
>>980 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:13:16.71 ID:BoJlALsC [2/20]
>>979 殺す
仮に同じとして差を取って微分すれば常に0になる
二つのグラフの差は定数
>>316 不連続のある関数なら定数は連続区間ごとに変えていいぞ
↑化け物がドアップで出てきてギャーーーーーって叫ぶ動画
>>559 4+7=11じゃなくて
Ω={(i,j)|1≦i≦4,1≦j≦7}から
#A=(4x7)-(3x6)=28-18=10により
∴Tの要素数の最大値は10
>>607 それだと5,7で1~24のとき最大値12が説明できないのでは?
■スイッチング関数
Table[2n-1+(-1/4+i/4)((-i)^(n-b)+i^((n-b)+1)+(-1-i)),{b,1,4},{n,1,10}]
Table[2n-1+{((n-b)+3)mod4},{b,1,8},{n,1,10}]
二項定理と数列の性質なんですが、
X〔k+m]+Y〔k+m〕√5=(X〔k〕+Y〔k〕√5)(X〔m〕+Y〔m〕√5)
※〔〕は小文字
凄く簡単みたいなんですが、意味がわからないので教えていただけると有難いです
y=(2x+1)^2はy=0のときx=-1/2になりますが、頂点の座標は(-1,0)ですよね?おかしくないですか?
Table[2n-1+{(n-4)+3mod4}+C(1,n-9)((-1)^n+1)/2+C(3,n-8)((-1)^(n+1)+1)/2,{n,1,10}]
{1, 4, 7, 10, 9, 12, 15, 18, 20, 21}
☆☆☆
Table[2n-1+{(n-2)+3mod4}+C(1,n-6)4((-1)^(n+1)+1)/2,{n,1,10}]
{3, 6, 5, 8, 11, 14, 17, 16, 19, 22}
>>616 Table[2n-b+{(n-1)mod4}+4C(0,n-9),{b,0,1},{n,1,10}]
{2, 5, 8, 11, 10, 13, 16, 19, 22, 21}
{1, 4, 7, 10, 9, 12, 15, 18, 21, 20}
1の4乗根て±1と±iですよね。
「4√1(←4×ルート4じゃなくて、√の左に小さい4のあるヤツ)はいくらか?」て書いてあったら
何と答えるのか教えてください。
自分としては「1」だと思いますが間違ってますか?
それで「-4√1」だったら「-1」だと思うんですが?
あと「-4√1」みたいな書き方で「+i」とか「-i」て答えなければいけない書き方てあるんでしょうか?
証明問題で、よって,ゆえに,したがって、といった接続詞を全て∴の記号に置き換えても問題ありませんか?
そもそも 故に 従って とか単に記号に置き換えてもよさそうな所にわざわざ書く必要ないよ
質問系スレッド18あるうち、ここが一番近いと思ったのでお借りします
(万一スレチならすいませんがスルーお願いします)
三点A,B,Cがあり、AB=AC=BCの場合、この図形は二次元の正三角形である
四点A,B,C,Dがあり、AB=AC=AD=BC=BD=CDの場合、この図形は三次元の正四面体である
五点A,B,C,D,Eがあるとする
AB=AC=AD=AE=BC=BD=BE=CD=CE=DE を満たす場合、
その図形は四次元(またはそれ以上)空間の図形になるでしょうか?
もしそのような図形がある場合、各頂点の座標はどうなるでしょうか?
>>624 そうだね 実際必要不可欠だと思う? 無いと意味変わるかな?誤解されるかな?
同値変形であるのかないのかとか 何故その変形が許されるのかとか その手の事に比べたらホントどうでもいい事だと思うよ
次の問題の解き方を教えて下さい。
【問題】
箱Aの中に10円硬貨、50円硬貨、100円硬貨がそれぞれ34枚・30枚・35枚入っています。
これに対し次の操作を繰り返し行う。
操作
2種類の硬貨を1枚ずつ箱Aから取り出し、代わりに先ほど取り出さなかった種類の硬貨2枚を,箱Aに入れる。
たとえば10円硬貨、50円硬貨を1枚ずつ箱Aから取り出したとき、代わりに100円硬貨を2枚箱Aに入れる。
このとき、箱Aの中の硬貨を1種類だけにすることができるか。できるならば、その具体的な手順を説明せよ。
できないならば,そのことを証明せよ。
出来ないような気がするが証明が合ってるかどうかよくわからない
その操作によって2種類の硬化の枚数の差は変わらないか3変わるかどちらか
現在の差は1、4、5なのでどの2種類もその操作を何度繰り返してもその差が0になることはない
最後に1種類だけになるにはそれ以外の2種類を1枚ずつ取り出しその2種類が0になる場合だけだがそうすると2種類の差が0であるときがあったことになり矛盾する
(10円玉の枚数) + (50円玉の枚数)*2 という値(Xとしよう)を考えると
10円が増える操作では変化しない
50円が増える操作では3増える
100円が増える操作では3減る
いずれにせよXを3で割った余りは変化しない
終了状態(いずれかのコインが99枚)でXは3の倍数
初期状態でX=94 は3で割って1余るので不可能.
>>630-631 どうも有り難うございます。
3で割った余り(3の剰余系?)で分類すれば良い訳ですね。
背理法になりますかね。
Table[2n-b-a+{(n+a)mod4}+4C(0,n-8+a),{a,0,1},{b,0,2},{n,1,10}]
{3, 6, 9, 8, 11, 14, 17, 20, 19, 22}
{2, 5, 8, 7, 10, 13, 16, 19, 18, 21}
{1, 4, 7, 6, 9, 12, 15, 18, 17, 20}
{3, 6, 5, 8, 11, 14, 17, 16, 19, 22}
{2, 5, 4, 7, 10, 13, 16, 15, 18, 21}
{1, 4, 3, 6, 9, 12, 15, 14, 17, 20}
高校数学じゃなかったらごめんなさい
n分の1の確率であたるくじをn回ひいていちども当たらない割合をAとすると
A=(n-1 )^n /n^n
ここでn→∞のとき近似値は0.37は有名だけど、Aは計算で展開できますか?
ありがとうございます!電卓たたいたら本当でした、知らなかった➰
えっ知ってて0.37って言ってんじゃないの?
A=(n-1 )^n /n^n=((n-1)/n)^n
=(1-1/n)^n
=(1+1/(-n))^n
=[(1+1/(-n))^(-n)]^(-1)
n→∞で[]の中がeになるから1/e
>>637 知らねーから質問してんだろーが
そして教えてやったら「知らなかった」といって喜んでんだろ
どう超解釈したら「知ってて言ってる」になるんだよ
いっかい精神病院いってこい
別に展開してるわけじゃないし1/eの方が0.37より有名だよ
どこで聞いていいかわかりませんが
高専ではフーリエや線形代数は習いますか?
>>641 習うけど大学でやるのと比べると程度は抑えられている
ふわっとした質問で恐縮なんだけど
関数の最大値最小値を求める数1の問題と
領域を求める数2の問題って似たような感じがするんだけど
違いってあります?
領域に境界が含まれるか否かを確認しなければならないのが最大最小問題の肝かな
ww.sankei.com/premium160627/prm1606270012-a.html
嘘つきマスゴミ障害者ウヨ猿産廃便所紙ゴキブリの人皮を剥がせ
ゴキブリ産廃便所社員を死刑にしろ
(2^(m+1)-2)/m が整数になるような自然数mは
1,2,6 の先にもまだまだありますか。
>>648 無数にある。
n≧0 のとき m=2×3^n はその性質を満たす。
なんと。そうなんですか。
これは簡単に示せるのですか。僕には無理?
1以上22以下の自然数の集合をSとする
Sの部分集合Tで、次の条件を満たすものを考える
[条件] Tに属する任意の2つの要素の差は4でも7でもない
Tの要素数の最大値はいくらか
1 5 9 13 17 21
2 6 10 14 18 22
3 7 11 15 19
4 8 12 16 20
aを定数とする。0≦x≦1のとき、関数y=-4^x+a*2^-x+2の最大値とそのときのxの値を求めよ
2定点A,Bと直線Lが与えられたとき
(例として座標表示でA(-1,0), B(1,0), L:y=x+4 とします。)
AとBを通りLに接する円を定木とコンパスで作図するにはどうすればいいですか。
>>657 AP = (PとLの距離)
を満たす点の軌跡を求めて(放物線) y=x+4 との交点求めればいいんじゃない?
>>659 求めた点は2次方程式の解なんだから作図できるじゃん。
数値的に解いた結果が作図できるというのと
作図的に解くというのは違うのでは?
>>657 直線ABとLの交点をCとおく。
CA・CB=CT^2を満たすTを作図する。
具体的には|CA|,|CB|を直角を挟む直角三角形を作図し、その外接円に内接する正方形を作図し、その一辺の長さaをとり、CT=aとなる点をとる。
△ABTの外接円が求める円。
Tは2つあるので円も2つできる。
質問主657ではないけど
なるほど方べきか
使い方が上手いなあ
本気で感心した
けっこう難しく手がかかるものなのですね
ありがとうぼざいます
すみません。下記の問題の解き方を教えて頂けないでしょうか。
【問題】
正四面体の各頂点をABCD、各頂点から等距離にある中心点をEとする。
中心点Eから各頂点への距離が30cmのとき、以下の問いに答えよ。
① 正四面体ABCDの一辺の長さを求めよ。
② 正四面体ABCDの高さを求めよ。
③ 正四面体ABCDの体積は、四面体BCDEの何倍か答えよ。
頂点座標が(0,0,0),(0,x,x),(x,0,x),(x,x,0)の正四面体を考えると、
一辺の長さ、体積、中心点から頂点への距離は簡単に出せる
前
>>186 >>665 ②中心Eは正四面体ABCDの重心で、4つの頂点からそれぞれ向かいあう面に引いた4つの高さはすべてEで交わる。正三角形の重心が正三角形の3つの高さをそれぞれ2:1に分ける点で交わることから、Eはその3つの高さをそれぞれ3:1にわけるはず。
(たとえばベクトルで表すと→AB/3+→AC/3+→AD/3=→AE=→3AH/4)
∴30(㎝)×(4/3)=40(㎝)
③底面の△BCDが共通で、高さが4倍だから、体積は4倍。
①正四面体ABCDの一辺をxとおくと、面の高さ、たとえば辺BCに対する頂点Aの高さは、BCの中点をMとして、
AM=(√3)x/2
MH=(1/3)MD
=(1/3)AM
=(√3)x/6
△AMHにおいて三平方の定理より、
AM^2=AH^2+MH^2
3x^2/4=40^2+3x^2/36
27x^2-3x^2=1600・36
24x^2=1600・36
x^2=800・3=2400
∴x=20√6(㎝)
以下の問題の答えを教えてください
白、青、緑、赤に塗られたボールが箱にたくさん入っている。
ボールが全部でいくつあるのかは分からないが、
全部の個数に対するそれぞれのボールの割合は
白……58%
青……29%
緑……10%
赤……3%
箱から無作為にボールを1個取り出すのを4回繰り返すが、
1個目のボールを取り出した後箱の中の赤のボールを全て取り除き、
2個目のボールを取り出した後箱の中の緑のボールを全て取り除き、
3個目のボールを取り出した後箱の中の青のボールを全て取り除く。
このとき4回連続で白のボールを引く確率は?
>>673 ボールが整数個であるためには
全部の個数が100nである必要がある
>>674(≒22.69%)はn=1における確率だが
nを大きくしていくと
極限1682/7275(≒23.12%)に漸近していく
というか
>3個目のボールを取り出した後箱の中の青のボールを全て取り除く。
この設定なしで「3回連続で白をひく確率」でいいのでは?
>>674 >>675 ありがとうございます
>「3回連続で白をひく確率」でいいのでは?
それはレスしてから気づきました
>>673前
>>672 lim(x→∞)58(0.58x-1)(0.58x-2)/(0.98x-1)(0.87x-2)
lim(x→∞)(195112x^2-10092x+20000)/(8526x^2-28300x+20000)
微分して(195112・2x-10092)(8526x^2-28300x+20000)-(195112x^2-10092x+20000)(8526・2x-28300)=0
(390224x-10092)(8526x^2-28300x+20000)-(195112x^2-10092x+20000)(17052x-28300)=0
(97556x-2523)(8526x^2-28300x+20000)-(195112x^2-10092x+20000)(4263x-775)=0
4回連続白が出る確率を考える。
1回目は0.58x個あった白が
2回目には(0.58x-1)個、
3回目には(0.58x-2)個と減っていて、
4回目をとるときは、
(0.58x-3)個ある。
全体の個数は、
2回目には赤3%を除き、97%になる。
3回目には赤3%と緑10%の合計13%を除き、87%になる。
4回目には赤3%と緑10%と青29%の合計42%を除き、58%になる。
つまり(0.58x-3)個、
これは白の数と同じ。
4回目は100%白が出る。
x=100のとき、
58・57・56/96・87=133/6
=22.166……
x=200のとき、
58・115・57/193・86=29・115・57/193・43
=190095/8299
=22.905771……
x=300のとき、
58・174・173/290・259=174・173/5・259
=30102/1295
=23.244787……
前
>>677訂正。
1も2も全体の数xと比べてじゅうぶん小さいから、
(58^3/97・87)・100
=58^2・200/97・3
=11600/291
=23.120274……
前
>>678修正。
=58^2・200/97・3
=58・11600/291
=(58000+5800+34800)/291
=(63800+34800)/291
=98600/291
=23.120274……
e (ネイピア数) = 2.71828,,,, と言うのがありますよね。極限の式
(1 + 1/n)^n
lim n → ∞
で、得られる数値ですが、これの n を x に置き換えた指数関数として y = (1 + 1/x)^x を考えます。
先の極限の式は有名なので、y = もよく扱われているだろう。と思っていました。
そこで、グラフで見たいと思いネットで探しました。しかし、指数、対数の一般的な
グラフはあるのですが、ピッタリのグラフは見当たりません。
そこでお願いです。
y = (1 + 1/x)^x のグラフのあるサイトを教えて下さい。
または、この式のグラフが描けるツールを教えて下さい。
一応、ツールも簡単ですが探しましたが、一般的な指数、対数のグラフ用で
求める式のグラフ作図は出来ない印象を受けました。
n つまり x は 1-20 程度を考えています。
宜しくおねがいします。
>>681 ありがとうございます。エクセル はちょっと面倒かな
>>682 これは良いですねー。ありがとうございます。
>>680 log y=xlog(1+1/x)=(log(1+t))/t (t=1/x)
>>684 回答ありがとうございます。
log で見るというのは、違った視点ですね。
参考になります。
Aとkとcを自然数とするます。
kA + 1 と A^c は互いに素というのは明らかにいえますか。
>>689 最大公約数が1より大きいならば, 公約数のなかに素数が存在するはずである(最大公約数の素因数分解を考えよ).
ここでA^cの約数のうち素数であるものdを適当にとってくると, これはAの約数である.
一方でkA+1をdで割ると1余るのでdはkA+1の約数でないので, 素数であるような公約数は存在しない.
すみません。適当なスレが見当たらないのでここで質問させてください
totoBIGの確率の話なのですが
BIGは14個の数字全て当たる確率が約480万分の1(一等)
14個のうち1つ外れて13個当たる確率が17万分の1となっています。(二等)
そして、当選金額の低いBIG1000では、11個の数字全て当たる確率が約17万分の1(一等)となっており、BIGの二等と同じ確率なのです。
14個中13個の数字を当てるのと、11個中11個の数字を当てるのは同じ確率なのでしょうか。
>>691 なんなら14個中13個あてる確率の方が若干高いよ
体感的な説明としては
14個のうちどれを外すかだけで14通りもあるし
その外したものをどう外すかのレパートリーも多い
totoだと三択だから 正解はひとつしかないけど
外す選択肢はその2倍あるわけだからね
>>691 だいたい同じなだけだね
totoBIGは2*14/3^14=1/170820.3214285714285714285714……
BIG1000は1/3^11=1/177147
totoのサイトでも上は約1/17万、下は1/177147となっていてピッタリ同じとは書かれていない
>>692 >>693 なるほど、ありがとうございます。
>>690 ありがとうございます。
あとこれはA=1でも成り立つるとして良いのですよね。
y=(log^2)^2の微分をどなたか教えてください
こんなん教師にでも質問するかwolframなりmaximaなり使えば一発でわかるだろ
わざわざガイジがガイジにマウント取るためのバトルフィールドで出すようなもんじゃない
AとBが互いに素で、DがAの約数なら、DとBも互いに素ですか?
「11の次に大きい素数は?」 日本人の78%が間違えた問題が話題に
http://2chb.net/r/news/1557483808/ nが自然数のとき、n^2が8の倍数ならnは4の倍数であることを示せ。
これを次のように証明したのですがこれでいいでしょうか。
(証明) n^2=8m (mは自然数)とおける。
n = √(8m) = 2√(2m) となる。
nは自然数だから、mは「2×(平方数)」の形である。
よってm = 2×k^2 (kは自然数)とおける。
n = 2√(2m) = 2*2k = 4k となるので、nは4の倍数である。
よろしくお願いします
1次試験参加者の最終試験合格率 10/86
2次試験参加者の最終試験合格率 10/46
1次試験から2次試験への合格率いくつでしょうか?
約52%だと計算したのですが、如何でしょうか?
>>704 論理に飛躍がある
√(2m)が自然数かすら分からん
n = 4k + r (0≦r<3) とすると
n^2 = 8k(2k+r) + r^2 ≡ r^2 (mod 8)
題意より r^2 ≡ 0 (mod 8)
r = 0,
nは4の倍数。
合同式使うならその余り置かずにやれるし、余り置くなら合同式は蛇足
あそうか
n=2√(2m) が整数だからといって、√(2m)が整数とは限らず
√(2m) が 半整数の可能性もある、ということですね。
その場合は √(2m) = k/2 とおいて2乗すると 8m = d^2
あああ元に戻っちゃった・・・
つーか証明なんて
これで良いのでしょうか?ってレベルの奴じゃダメだよ元から結果は分かってるような事いうなら余計に
動揺してます 8m=d^2 じゃなくて 8m=k^2 ですた
自分が混乱するなら、あまり良い証明ではないのでは。
試験では解答できなさそう。
/_/_/人人_/_/_/_
/_/_(_^_)/_/_/_
/_/_(__)/_/_/_
/_/_((^。^)/_/_/_
/_/_(_っ-┓_/_/_
/_/_◎゙┻υ◎゙/_/_/_/_/_/キコキコ……/_/_/_/_/_/_/_/_/もっと先のその先へ。前
>>679加速してみたくはないか。
10%の食塩水1kg作るのに必要な塩と水は? 大学生が「%」を分からない絶望的な日本【ゆとりw】
http://2chb.net/r/news/1557794917/ 前>>715
>>716、,
((-_-)
(っц)~
「 ̄ ̄ ̄]ビーカーに塩100gを入れ、メスシリンダーで水900ml測りとり、これを注ぎ溶かす。
10%は塩辛い。 >>704 nは自然数だから→m,nは自然数だから
にすれば、nが自然数だから√2を消すパターンと(√2)^=2を作るパターンがあるが、
mも自然数なので後者しかありえないと主張したことにはなるが、
そこまであなたはわかってないんだよね?
二次関数が分からなさすぎる
みんなどうやって理解してるのか不思議でしょうがない
コツとかあるんかな
前
>>717 y=c(x-a)^2+b
点(a,b)を頂点とした放物線。世界がこんな典型的な関数ばっかりだったら楽だな。
>>719 高校数学の基本のきだからかなりの理解が必要。
まあがんばれ
√(2*10^n + 5) が有理数になるような自然数n は1だけでショウか。
無限級数の質問です
Sn = Σ(-1)k n→∞
これが偶数と奇数の時0と-1になるのはわかるんですが、これって振動じゃないんですか?
発散って書いてあってちょっとよくわかりません
>>726 教科書に書いてあるから、ゴミみたいな問題集や参考書に頼ってないで教科書よめ
>>726 数列が発散するとは、数列が収束しないこと
数列が振動するとは、数列が収束も正の無限大への発散も負の無限大への発散もしないこと
つまり、振動は発散の一形態
>>719 定数を含む二次関数の場合分けが理解できるか否かが以後の数学学習の
ひいては人生の分かれ目といっても過言ではない

(4)の解説お願いします…おきかえがうまくいかないです
すみません、もしかしたらめちゃくちゃ簡単なことを聞いてるかもしれませんが、画像の問題をお願いします

ある関数のグラフとy=xに対称なグラフってのは
逆関数のグラフってのは知識
指数関数の逆関数が対数関数なのも知識
それはおいといて今回の問題はPと軸に対称な点Qを考えてPQの長さが1番短いってことだから
Pが一番対称軸に近い所考えてねってこと
一番y=xに近い点考えたらいい
点と直線の距離公式でも使ったら?
>>749 p/qとおく
>>750 PQの距離=(y=2^xとy=xの距離)×2
>>750 その曲線のグラフを考える
その曲線とy=xとの距離が求まればよい
その曲線の傾きが1となる点を見つければよいってことなんじゃ?
>>749 n≧2 において
2*10^n + 5 は 5 の倍数であり
かつ 25 の倍数でない
ありがとうございます
これ数3の微分必要になりますか?
>>749 2*10^n + 5が平方数になればいい
2*10^n + 5は5を因数に持つ奇数であるのでこれが平方数であるとき25*(2m+1)と表せる(nが2以上のときmは正の整数)
2*10^n + 5はnが2以上のとき十の位が0であるが、25*(2m+1)=50m+25はmが正の整数であるとき十の位が0になることがない
>>754 ああそうか
それだけでいいのか
自分のはどうもブサイクな証明だなと思っていた
暗記でしょうか、公式はそうかもしれませんが
それがテストでできるようになるまでの膨大な計算量と(時々部分的に理解が詰まる部分と)
その奥底にあるものがなんであるか考えてしまう部分とで難しく感じます
>>761 ただの暗記ではないね
ちょっと応用する習慣があるだけで暗記すべきことは格段に減るし
パターンを暗記してもそれをあてはめるための判断力がないと意味が無い
逆に本来ならケースバイケースで状況を見て応用を考えるべき部分を
いくらか類型化して割り切って暗記で進めることで理解も効率的に進むこともある
両輪がないとどっちかに偏ってるとかなり苦しむだろうね
あと忘れられがちだが机上の空論にばかり走ってて
初歩過ぎる要素(たとえば単純な計算力)が鍛えられてないと
そのせいで発想や判断、暗記するにあたっての整理の仕方などにも影響が出ることもある
まぁ1a2bならおっしゃる事も分からんでも無いけど
入試の数三なんてパターン暗記色はその他の分野以上に強いよ
そもそも要求される作業量多いしチンタラ考えてるような奴は処理しきれん
>>750ですが、答えかなり汚い式になりますか?
微分してもらちが明かないので、直線y=x+pがy=2^xと接すると考え、連立して
2^x=x+pが重解をもつ、つまり判別式=0
からpを求めると考えたんですが(これなら数3使わなくて済みそう)
この場合だとここからどうすればいいでしょうか
>>765 二次関数でないのに判別式ってどういうこと?
数学脳は人それぞれで暗記でこなすタイプの人などいろいろなタイプの人がいるのかなと思いました
数3なんて理解できんよ
説明不足にもほどがある
暗記するだけ、理解とか言ってる奴は理解したつもりになってるだけ
>>772 問題の難易度としてはそうかもな
脳みそ空にして計算だけ繰り返すのは確かに小学低学年の算数
受験生は忙しいから理解はな~
大学生になってから暇に任せて研究するといいのかな
積分計算の工夫もパズル感あるしな
1a2bまでの理詰めで出てくる工夫と違って
知らんと時間内には気が付かない系のオンパレード
パズルというより型を覚えているか否か
微分することと異なり積分は原始関数が知られているものしかできないわけだから
高校の積分すらマスターできないアホがパズル本見ても無駄
札南>札北>北嶺>札西>札東>旭川東>帯広柏葉>旭丘>国際情報>月寒
これが北海道の学力トップ10
渋幕>市川>県千葉>東邦>船橋>秀英>専修松戸>東葛飾>佐倉>千葉東
これが千葉県の学力トップ10
整数を余りが0のものと1のものと2のものに分けるってことだよ
鳩ノ巣原理でピジョンボックスに割り振って適当な代表元としてハッシュ値を割り振るということだよ。」
急いでます。
ψ(x.t)=Asin(2π/λ・x-2π/T・t)
をxで二回偏微分すると、どうして
-(2π/λ)^2ψ(x.t)
になるのですか? 途中計算わかるひといますか?
tは定数とみなしてxで微分するだけ
あとはsinの中をf(x)と置いて合成関数の微分をすればよい
>>786 なぜ高校数学の質問スレで偏微分を聞くのか
高校数学に偏微分なかったんか
分ける意味が分からんな
2変数だからです、これ以上はスレから外れるので無視してください
高専の方は忖度しないと住民に殺されるので、注意しましょう
三角形ABCにおいてa=√3 B=45° C=15°の時
辺b=√2になるのですが
辺cを出すときにBを使って答えを出そうとすると(√6±√2)÷2という答えが出てきます
しかし解説と解答を見るとAを使って(√6-√2)÷2という答えにしかなりません
この場合は前者の答えは間違いになるのでしょうか
またそれはなぜでしょうか
よろしくお願いします
>>796 三角形の合同条件
∠B=45°、a=√3、b=√2という三角形は2通り描けるだろう?
これらだけを条件にcを求めたら2通り答えが出てくるのは当然
>>797 ありがとうございます
「三角形が1通りとなる要素」が問題から得られていないので
最初にBをつかって±となる答えがでてしまったら
もう一方の方(A)で計算しろということでしょうか
Aを使えばc>0であることから
計算で出せた±のうちの+の数に限定できます
その場合、二度手間になりますが
一発目で決めることはできないんでしょうか
補足
実際には二辺とその間の角が解るので「三角形が一通りとなる要素」は満たされているのですが
15°では余弦定理が使えないので
>>798の考え方になるんでしょうか
>>798 三角形の頂角の大小と対応する辺の大小の関係から、一方は捨てられる。
15の倍数の角度は知らなくても求められるというのは常識にしておかないとまずい
普通に出るぞ
15度なんて初見でと45-30とか 30/2 とか いくらでも作り方思い浮かびそうなもんだが
36度とか72度なんて作れねぇってならまだ同情の余地があるけど
>>810>>811
まあ中学の三平方で済むわけだけど
結局三角比の初歩での数値計算練習だとどうせ15の倍数角くらいしか使わんから
796にとって三角比の正弦定理余弦定理などをどう使うかの練習・その過程で出てきた疑問を考えるという意味なら
三角比でやる意味はあるだろう
>>798 まず余弦定理の二次式で解が2つ出たのは
>>797の言うとおりで
その二次式にはC=15°の条件が反映されてないから2通りになる
(形によっては0や負になるのでその場合は話が早い)
ともに正の解になった場合もそのあと計算するまでもなく
>>800で分かるが
ためしに
>>797の条件でどういう形で三角形が2つできるのかを自分で作図してみれば
(先にBCを描いておいてコンパスで点Aを作図することをイメージしてみれば)
2つの解がどういう状況なのかが簡単に理解できるよ
簡単な問題には即座に解答がつき解答者は大人ぶる
これが数学板の実力です
専門板なのに異常にレベルが低い
せいぜい数学の少しできる高校生レベル
そもそも高校数学の質問スレで量子力学の問題を乗せること自体おかしい
>>800 >>803 やっと理解できました
意外に二通りあるんですね
ありがとうございます
15°もついでに覚えておくことにします
スキームを関手として定義している本がありますが
どういうことなんでしょう
等式の変形 ってのが良くわからんのだが
左辺と右辺をそれぞれ微分や積分しても一緒なのか?
四則演算以外に何が出来るんだよ
元々同じものなら全く同じ操作をしたって同じものになるのは当然だろ。
もし違うとしたら同じ操作をしてないか
もともと違ったものだったかだけ
でもさ、左辺が関数で右辺が0とするじゃん
この場合、両辺を何回でも微分しても、
その全ての等式って必ず成立するってことか?
恒等式と方程式の区別が付いてないのでは?
x=3
とか3x=9とかのxは変数じゃないから
xで積分とか微分はナンセンス
>>818 ある無矛盾な公理系τの任意のモデルに対してある論理式φが常に真となるならば、τからφがLKにおいて証明可能となることを示せ
>>819 何で示す必要あるのかはやく答えろよゴミカス
>>819 毎度毎度逃げるのかよ
オメエも死んどけやクソゴミが
あれ?一時期シーフの話にいったんじゃないの?また完全性定理に戻ってるよ。
>>978 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 00:59:28.70 ID:BoJlALsC [1/20]
>>977 >より進んだ数学の中には、多項式としては 0 ではないが、それを多項式関数と見た場合は 0 というようなものがある。
ありません
複素関数を考えるにしても、多項式、すなわち連結領域上の正則関数を考えるならば、一致の定理よりある部分で0なら全体で0です
多項式とは有限次元で打ち切りですから、収束半径は無限大、すなわち複素数全体で0となります
>>979 自分:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:11:11.10 ID:MxKVVcoK [2/4]
>>978 標数2の素体上で多項式関数 x^2+x を考えると、これは常に0関数となります。
>>819 標数もしらない無知無能のクソ猿がwww
バカがなんでのうのうと生きてんだよ
うんこ製造してるだけの馬鹿なんだからさっさと死ね
>>825 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)
>>827 何で示す必要あるのか早くこたえろよゴミカス
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)
>>829 何で示す必要あるのか早くこたえろよゴミクズ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>831 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>833 何で示す必要あるのか早くこたえろよゴミカス
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>835 何で示す必要あるのか早くこたえろよゴミクズ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>837 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>839 何で示す必要あるのか早くこたえろよゴミカス
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>841 何で示す必要あるのか早くこたえろよゴミクズ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>843 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>845 何で示す必要あるのか早くこたえろよゴミクズ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>847 何で示す必要あるのか早くこたえろよゴミカス
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>849 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>851 何で示す必要あるのか早くこたえろよゴミクズ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>853 何で示す必要あるのか早くこたえろよゴミカス
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>855 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>857 何で示す必要あるのか早くこたえろよゴミクズ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>859 何で示す必要あるのか早くこたえろよゴミカス
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>861 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>863 何で示す必要あるのか早くこたえろよゴミクズ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>865 何で示す必要あるのか早くこたえろよゴミカス
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>867 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>869 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>871 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>873 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>875 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>877 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>879 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>881 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>883 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>885 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>887 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>889 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>891 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>893 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>895 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>897 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>899 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>901 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>903 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>905 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>907 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>909 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>911 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>913 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>915 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>917 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>919 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>921 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>923 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>925 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>927 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>929 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>931 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>933 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>935 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>937 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>939 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>941 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>943 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>945 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>947 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>949 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>951 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>953 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>955 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>957 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>959 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>961 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>963 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>965 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>967 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>969 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>971 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>973 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>975 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>977 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>979 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>981 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>983 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>985 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>987 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>989 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>991 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>993 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>995 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>997 何で示す必要あるのか早くこたえろよゴミ
つまり、わからないと言うことですね(笑)(笑)(笑)(笑)(笑)
>>999 何で示す必要あるのか早くこたえろよゴミ
このスレッドは1000を超えました。
新しいスレッドを立ててください。
life time: 123日 21時間 15分 52秒
5ちゃんねるの運営はプレミアム会員の皆さまに支えられています。
運営にご協力お願いいたします。
───────────────────
《プレミアム会員の主な特典》
★ 5ちゃんねる専用ブラウザからの広告除去
★ 5ちゃんねるの過去ログを取得
★ 書き込み規制の緩和
───────────────────
会員登録には個人情報は一切必要ありません。
月300円から匿名でご購入いただけます。
▼ プレミアム会員登録はこちら ▼
https://premium.5ch.net/ ▼ 浪人ログインはこちら ▼
https://login.5ch.net/login.php
lud20250729124106caID:C5mohd4sのレス一覧:
>>132 θ=π/2+2nπ ±i*log(2+√3)
cosθの候補がもう一つあるのをお忘れなく。
>>163 今さらだけどダイアグラムを知らなくても似たような考え方で出会ったのが中間点だということはわかるよ
BがスタートしたときにAがいる位置をR、BがゴールしたときにAがいる位置をSとすると、PRもSQもAが1時間かけて進む距離だから同じ
従ってRSの中点はPQの中点と一致する
BがQをスタートしてPに到達するまでの間にAはRからSに進んでいるわけだが途中はどうなっているのか考えると
Aが中間点に到達する前はBも中間点に到達せず、Aが中間点に到達したときBも中間点に到達、Aが中間点を超えたらBも中間点を越えている
つまり、出会うのは中間点
イキるのはいいが
>>164-165あたりを見てもう一度考えたらどうだ?
>>170 同じ距離を互いに端からすすむのだからその図で問題なかろう
反論はよ
計算問題で「そこ、符号の+と-が違ってるよ」って注意したら
「数字が合ってるから問題ない、反論はよ」って返す奴か
厄介だな
というか水槽ニキの設定なら 誰も悩まずにダイヤグラムなんて書くことなく処理できるんだよなぁ
【池江の白血病、科学的見解】 飛行機での移動で宇宙からの放射線を浴びたせい、福島原発ではなく
http://2chb.net/r/liveplus/1550460074/l50 階級値に関わる質問です。
身長で150以上155未満(cm)の時は階級値は152.5(cm)なのはわかるのですが、たとえば参加人数のように整数値で10人以上15人未満のとき、階級値は10~15の中央値で、12.5となるのでしょうか。それとも10人以上15人未満なので10,11,12,13,14の中央値で12となるのでしょうか?
前
>>166 >>168数学的に数式と数値で示せると思う。
①より、
x=3V+3=3・3+3=12(㎞)
②より、
y=4V=4・3=12(㎞)
∴x=y
よってAとBはP市とQ町の中間点で出会う。
a^3+b^3+c^3-3abcの因数分解について質問です。
結果はもちろん、一般的な作り方も理解しています。
ただ、どこかで解と係数の関係をうまく使って作り出しているのを見たことがあって、それがどのようなものだったかどうしても思い出せません。
どのようなものかご存知の方いらっしゃいませんか?
a^3+b^3+c^3-abc 解と係数の関係
でググレカス
a^3+b^3+c^3-3abc = (a+p)(a+q)(a+r) とすると、
p+q+r=0, pq+qr+rp=-3bc, pqr=b^3+c^3=(b+c)(b^2-bc+c^2) … ①
ω=exp(2πi/3)として、p=b+c, q=ωb+(ω^2)c, r=(ω^2)b+ωc が ①を満たす
よって与式 = (a+b+c)(a+ωb+(ω^2)c)(a+(ω^2)b+ωc) = (a+b+c)(a^2+b^2+c^2-bc-ca-ab)
前
>>178 >>179 a^3+b^3+c^3+3abc
=(a+b+c)^3-3(a^2・b+a^2・c+b^2・c+b^2・a+c^2・a+c^2・b-6abc+3abc
(^ω^)
>>137 です。
数日経ってまたここを覗きに来ましたが、私の出した問題について揉めている?ような雰囲気になっていて驚きました。皆さんのおかげで理解出来たので感謝しています。どうせggrksって言われて終わりだろうなと思っていたので。
高校生に恥をしのんで聞いてみてよかったです。
考えてくれてありがとうございました。
ですのでどうか、揉めるのはおやめください。
0<x<1において
2^x>x^2+1が成り立つ
これを文系の範囲で証明できませんか?(数Ⅲ微積は未履修です)
前
>>183 >>185 y=2^xのグラフと、
y=x^2+1のグラフを書いて、
0<x<1においてどっちがおっきいか調べたらわ?
あいだどんなけ刻めるかやね。
絶対値が4より大きく7以下の整数の個数という問題なんだけど、
これいくつになるの?6個?
>>186 あいだを何個かとって大体成り立つだろうという予想は立ててるんですが、証明ができなくて困ってます
数Ⅲやるしかないんでしょうか
どういう状況で質問してんの?
受験でこれに対応したいってなら微積やった方が圧倒的に早いでしょ
例え上手い方法を誰かに教えて貰ったからといって自分じゃ絶対気が付けないしなんの汎用性もないからな
>>185 あらすじを書くとこう
・f(x)=2^x-(x^2+1)とおく。f(x)は0<x<1で連続かつ(少なくとも)2回微分可能
・0<x<1でf''(x)<0、よって0<x<1でf'(x)は単調減少
・f'(0)>0,f'(1)<0、よって0<c<1かつf'(c)=0となるcがある
・f(0)=0かつ0<x≦cでf'(x)>0、よって0<x≦cのときf(x)>0
・f(1)=0かつc≦x<1でf'(x)<0、よってc≦x<1のときf(x)>0
・よって0<x<1のときf(x)>0
・よって0<x<1のとき2^x>x^2+1 □
文系で理解できるかどうかは努力しだいかな
>>192 春休みの自由研究の途中で出てきた不等式です
大学付属校なので受験はしないです
なので数Ⅲをやるつもりは今のところありません
所詮自由研究なので、この不等式が成り立つことを認めた上で論理展開しても構わないんですが、
数Ⅱまでの知識でも証明できるならしておきたい(知りたい)ってだけです
>>193 文系向けに噛み砕いてみる
数学的に厳密でないかもしれないけどご容赦。
・(左辺)>(右辺)を証明したいので、f(x)=(左辺)-(右辺)と置いてみる。0<x<1のときf(x)>0と言えれば元の命題が証明できる・f(x)のグラフを描いてみると、f(0)とf(1)がともに0であり、0<x<1ではf(x)がプラスであることがなんとなくわかる
・「0<x<1でf(x)がプラス」を証明するためにグラフの傾きを調べたいので、導関数f'(x)の様子を調べてみる
・f'(0)>0だから、x=0のところでf(x)は増加中、f'(1)<0だから、x=1のところでf(x)は減少中であることがわかる
・0<x<1のすべてでf(x)>0であると言うために、範囲の途中にf'(c)=0となるcがあって、0からcまではf(x)が増加、cから1まではf(x)が減少であることを示す
・そのために導関数f''(x)の様子を調べる
大学附属って文系でも数三までやらせられる所多いのに珍しいな。
経済とか商とか経営系でも四月頭からばしばし微積使うから純粋文学部以外は数三ぐらいは必須だからやるみたいな所の方が多いのに
>>189 >>190 やっぱり数学板って無能しかおらんのじゃないか?
絶対値の問題に詳しいひと 数学
http://2chb.net/r/news4vip/1550810571/ 公務員障害者採用試験スレ20【精神専用】
http://2chb.net/r/utu/1550803131/ なおここにもマルチで立てて質問してるが。
文系理系でもあまり出来や素質は違わないが、経験やカリキュラムの面で大きく差が出ているだけではないか?
>>197 これはニュー速で指摘されてる通りだね。
6個も、無限個も、日本語の解釈として有りうるのでどっちも正解になってしまう。
強いてどっちか一つ選ぶなら読点の存在から無限個の方を選ぶことになる。
指数関数の微分を数三だと扱わないってのと
ネイピア数を扱わないから自然対数取ることも出来ない
三次函数ぐらいの微積分なら文系もやる 笑
文系だと 2^x の微分ができないので増減表以前の問題。
2^xの凸性を認めてもらえるなら手はあるけどくだらない。
結局、数Ⅲまでやったらスパッととけて、数Ⅱまでだと無意味に難しい問題なんかそもそも意味ない。
文系・理系のカリキュラムも知らない馬鹿がなんでドヤ顔で講釈たれてるの?
「できません」→「この無能が」
「できます」→「なにそのドヤ顔」
これが数学板
無理ってことね。了解
>>193とか
>>195みたいな無能って何考えてんだろうな
誰の役にも立たない長文書いて
こっちは微積使うな(初等的に)ってオーダーしてんのに
無理なら無理っていえよ
バカには無理ってはっきり言ってあげた方が本人のためってことだ
a,bを整数の定数とし f(x)=x^2+ax+b とする。
任意の整数xに対してf(x)>0 であうことは、任意の実数xに対してf(x)>0 であるための( )
という問題で
答えは私は必要条件だと思ったのですが正答は必要十分条件らしいのです。
どうしてなんでしょうか。
数Ⅲやるつもりもない無能が教えてもらう人を無能扱いw
>>208 おそらく整数以外の部分でf(x)が0以下になる可能性がある
って考えて必要条件って思ったのだろうけど
a奇数で重解にするためにはbが整数に反するし
a^2-4bが整数である縛りから0<√D<1になり得ないから整数と整数の間だけx軸を切り取るみたいなのが無理
>>208 ちゃんと読んでいなかったすまん。
必要性は明らか。
十分性について、aが偶数の時は、最小値を取るxは整数になるので成り立つ。
aが奇数の時、xが整数ならば整数の掛け算なのでf(x)も整数。
よって、1/4-D/4≧1
∴D≦-3
>>208 >>211,212 さんの回答からわかる通り、これ、瞬間で答えるには結構難問だね。
問題文中の >0 が ≧0なら「必要条件」が正解になるところが面白い。
d^2yってグラフ的に何ですか
dxの2次関数と見なせますか?
211様212様ありがとうぞざいます。十分条件もいけるのですね。
それにしても入試でこの形式だと普通は必要条件のみ答えてしまうのではないですか。
ちょっと意地悪なカンジがすます。
Fラン文系用ならともかく、もし正解が必要条件なら何でもサル問題すぎて怪しいと疑わないか?
文系レベルのアホがゴミカス問題をいつまでも難しい難しいって騒いでて邪魔
>>219 おまえが211や212でなければそんなことを言う資格はなし
こういう奴に限って全然質問に答えられないんだよなw
そもそもなんの根拠もなく
「整数で常に正でも整数じゃないところじゃ負になるかもしれないんだから成り立たない!」
ってバカ丸出し。
そういうバカを振るい落とすために問題は作成されている。バカは一生苦しんどけ
馬鹿が発狂していてワロタ
この馬鹿が何か質問に答えられるかどうかが見ものだなw
>それにしても入試でこの形式だと普通は必要条件のみ答えてしまうのではないですか。
>ちょっと意地悪なカンジがすます。
何言ってんだコイツw
こいつ進研模試で50点も取れないアホなんだろうなwww
>>224 ある無矛盾な公理系τの任意のモデルに対してある論理式φが常に真となるならば、τからφがLKにおいて証明可能となることを示せ
>>978 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 00:59:28.70 ID:BoJlALsC [1/20]
>>977 >より進んだ数学の中には、多項式としては 0 ではないが、それを多項式関数と見た場合は 0 というようなものがある。
ありません
複素関数を考えるにしても、多項式、すなわち連結領域上の正則関数を考えるならば、一致の定理よりある部分で0なら全体で0です
多項式とは有限次元で打ち切りですから、収束半径は無限大、すなわち複素数全体で0となります
前スレ
>>979 自分:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:11:11.10 ID:MxKVVcoK [2/4]
>>978 標数2の素体上で多項式関数 x^2+x を考えると、これは常に0関数となります。
前スレ
>>980 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:13:16.71 ID:BoJlALsC [2/20]
>>979 殺す
代数の知識がかけらもないアホwwwwwワロスwwwwwww
ふつーに標数>0の話してるってわかるよなあ?
それを複素関数ってwwww
数学科すら出ていないウンコ丸出しでワロタ
ふっふっふっふっふくそかんすううううう?????wwwwwwwwwwww
長さxが与えられたとき、
x^2の長さの線分を作図するにはどうすれば
x=1ならそのまんま
x>1なら高さが1で面積がx^2の平行四辺形を作れば長辺の長さがx^2になる
x<1なら長辺が1で面積がx^2の平行四辺形を作れば短辺の長さがx^2になる
描き方は説明が面倒なので省略
こんなのしか思い浮かばなかった
>>235 相似を利用する
1:x=x:A
よって、A=x^2
こんなの教科書にのってるじゃん
236とか237とかは教科書も持ってないアホなおっさん
一点x=aのみで定義されている関数は
x=aで連続ですか
物のつながりを表す数学的構造のことです
連続性とは、そのような位相構造に基づき定義されます
↑これが数学板の実力です↑
専門板なのに異常にレベルが低い
せいぜい数学の少しできる高校生レベル
【超悪質!盗聴盗撮・つきまとい嫌がらせ犯罪者の実名と住所を公開】
①井口・千明(東京都葛飾区青戸6-23-16)
※盗聴盗撮・嫌がらせつきまとい犯罪者のリーダー的存在/犯罪組織の一員で様々な犯罪行為に手を染めている
低学歴で醜いほどの学歴コンプレックスの塊/超変態で食糞愛好家である/醜悪で不気味な顔つきが特徴的である
②宇野壽倫(東京都葛飾区青戸6-23-21ハイツニュー青戸202)
※色黒で醜く太っている醜悪黒豚宇野壽倫/低学歴で人間性が醜いだけでなく今後の人生でもう二度と女とセックスをすることができないほど容姿が醜悪である
③色川高志(東京都葛飾区青戸6-23-21ハイツニュー青戸103)
※色川高志はyoutubeの視聴回数を勝手に短時間に何百何千時には何万回と増やしたり高評価・低評価の数字を一人でいくつも増やしたり減らしたりなどの
youtubeの正常な運営を脅かし信頼性を損なわせるような犯罪的業務妨害行為を行っています
※色川高志は現在、生活保護を不正に受給している犯罪者です/どんどん警察や役所に通報・密告してやってください
【通報先】
◎葛飾区福祉事務所(西生活課)
〒124-8555
東京都葛飾区立石5-13-1
℡03-3695-1111
④清水(東京都葛飾区青戸6-23-19)
※低学歴脱糞老女:清水婆婆 ☆☆低学歴脱糞老女・清水婆婆は高学歴家系を一方的に憎悪している☆☆
清水婆婆はコンプレックスの塊でとにかく底意地が悪い/醜悪な形相で嫌がらせを楽しんでいるまさに悪魔のような老婆である
⑤高添・沼田(東京都葛飾区青戸6-26-6)
※犯罪首謀者井口・千明の子分/いつも逆らえずに言いなりになっている金魚のフン/親子孫一族そろって低能
⑥高橋(東京都葛飾区青戸6-23-23)
※高橋母は夫婦の夜の営み亀甲縛り食い込み緊縛プレイの最中に高橋親父にどさくさに紛れて首を絞められて殺されそうになったことがある
⑦長木義明(東京都葛飾区青戸6-23-20) ※日曜日になると風俗店に行っている
閉区間で微分可能は考えないのですか
|x|は[0,∞]が定義域ならx=0でも微分可能ですか
サイコロをn回振って出た目を全て掛け合わせた数の期待値って
(一回振って出る目の期待値)^nで合ってますか?
質問です。
瀬山四郎先生のトポロジー柔らかい幾何学の本を読んでいます。
10ページめの
"S^3は中身のつまった2個の3次元球面体の表面を貼り合わせて作られことになりますが.."
これはx^2+y^2+(z-2)^2=r^2 の rを[0,2),[2,∞)に分けることらしいのですが
なんで当たり前のことをわざわざ言うのでしょうか
まだ射影幾何的なことは出ていません。
S^2のときは、いいのですが、S3では球面をボールの外と同一視しているということでしょうか?
正六角形の辺をサイコロが出た目だけ反時計回りに回る
3回振って出発点に初めて到着する確率はなんでしょうという問題で
自分は1回目で6以外が出ればいいから5/6
2回目で、出してはいけない目は1つ(出発点に到着してしまう目)だから5/6
3回目は到着しなければならないからどの点にいても1/6
5/6×5/6×1/6で25/216となりました
答えはあっているのですが、模範回答には場合分けによる解法のみで、こんな解答は載っていませんでした
もしこの解答に抜け目があれば教えてください
教科書の樹形図の項目に問題があれば
全通りを図に書くのが正解となる
教科書・問題集の全体を晒さないと
判断できない
251に関連するんですが
サイコロをn回投げて出た目の総積が12で割り切れる回数の期待値
は
(4で割り切れる回数の期待値)*(3で割り切れる回数の期待値)
で合ってますか?
それは合ってないんじゃないか?
後者の方が大きくなるように思えるが
総積が2や3のような素因数で割り切れる回数の期待値ならすぐ求まるのですが...
2*3や2*2*3のように複数の素因数で割り切れる回数の期待値のときはどう求まるんでしょうか?
>>262 1/6×n以外での出し方考える事からはじめたら?
あーごめん1/6ではないか ただまぁいいたいのは一回辺りの期待値出してそれをn倍するみたいな方法でないってこと
確率について教えてください。
10000のクジの内、当たりが100枚の場合
当選確率は100/10000で、当選確率1%と表示されそうですが
実際にクジを購入する場合に1枚しか買わなかった場合
当選確率は1%になるのでしょうか?
このケースでは、100枚購入した場合の当選確率が1%だと思うのですが、どうでしょうか?
>>264 6と偶数
3と4
3と偶数2つ
で場合分けですかね?
ここから期待値を求める方法が分かりません
>>266 割り切れる回数をカウントしないといけないから
君のやり方だと12で割れるかどうかを考えるのには多少は役に立つけど
何回割れるかを考えるのには向いてないから
真面目にそれぞれ2,3,4,6が出る回数を考えて何回割れるか考察して それが何パターンあるかを考えるってのがいいと思うよ

違いを教えてください
30%、100個に30個、10個に3個は全て意味が違うのですか?
>>270 上はサンプルが大量にあって30%が不良品って分かってるケースで考えている
正確にはもし一個目に不良品を引いたら、二個目を引く時に全体の中から不良品が一個分少なくなっていてその分不良品を引く確率が下がってるはず。
しかし大量にあるなら大した影響は無いから無視できる。
下はサンプルがホントに100個しかなくて そのうち30個が不良品ってのが分かってるケース
でも不良品が30%と言われて全数が与えられていないなら通常は上で考える
なぜなら下で考えるにはサンプル数によって答えが変わるから
ここ話題がすぐ変わってつまらんな
単発スレ立てるは
二者択一の◯×問題の正解率がどの問題も等しく80%である時、
五者択一の正解率の求め方ってありますか?
例えば五者択一なのに、1問1問を二者択一で仮に回答を行ったところ、××◯×◯という回答をした時には「◯が2つは有り得ない、おかしい」という普通の判断を行うものとします
>>274 問題の前提がわからないのでこういう仮定をしてみる:
・正答を知っている回答者は必ず正答を選ぶ
正答を知っている回答者の正答率は1/1
・正答を知らない回答者は選択肢を無作為に選ぶ
正答を知らない回答者の正答率は二択卓なら1/2、五択なら1/5
・上記2通りのどちらか以外の回答者は居ない
回答者のうち正答を知らない割合をxとすると、
二択の場合の正答率は(1/1)(1-x)+(1/2)xで、
五択の場合の正答率は(1/1)(1-x)+(1/5)x
>>274 設定がよくわからない
どんな問題であろうと二者択一なら必ず8割正解出来る人物が存在するという仮定してその人物が五者択一問題をどれくらいの割合で正解出来るかってこと?
家庭に無理あるんでないんだろうか
>>275 >>276 申し訳ない
~~は◯か×か?という問いの正解率が80%の前提
次の5択の中に正解は1つ
a、~~は◯である
b、~~は×である
c、~~は◯である
d、~~は◯である
e、~~は×である
~~で省略しましたが全部違う問いです
この五択の正解率は導けるのかなと思っての質問でした
アンパンマンはパンである◯か×か
カレーパンマンはラーメンである◯か×か
食パンマンはそばである◯か×か
チーズは犬である◯か×か
ジャムおじさんはおばあさんである◯か×か
このような一問一答の正解率が80%の人がいて、この一問一答で構成された五者択一
a、アンパンマンはパンである
b、カレーパンマンはラーメンである
c、食パンマンはそばである
d、チーズは猫である
e、ジャムおじさんはおばあさんである
の正解率が導けるのかなと思っての質問です
この正解はaですが、仮にaとbの両方が正解だと思っても、両方は有り得ないだろう、という判断が前提となる話です
そんなの仮定出来るのかなあ?
二者択一を50万問やるとだいたい10万問間違える
正解は教えずに、間違えた10万問だけ別の問題に差し替えて再び50万問やらせたらどうなるんだ?
正解の選択肢をaと仮定しても構わない。解答にaを選ぶ可能性があるのは次の2パターンである。
i. 選択肢を読んでaを○と判断した場合
(1) 他の選択肢をすべて×と判断した場合: (4/5)^5
(2) 他の選択肢に1つだけ○と判断し、1/2の確率でaと解答した場合: (4/5)×4×(4/5)^3×(1/5)×(1/2)
(3) 他の選択肢に2つだけ○と判断し、1/3の確率でaと解答した場合: (4/5)×6×(4/5)^2×(1/5)^2×(1/3)
(4) 他の選択肢に3つだけ○と判断し、1/4の確率でaと解答した場合: (4/5)×4×(4/5)×(1/5)^3×(1/4)
(5) 他の選択肢もすべて○と判断し、1/5の確率でaと解答した場合:
(4/5)×(1/5)^4×(1/5)
ii. 選択肢を読んですべて×と判断し、1/5の確率でaと解答した場合: (1/5)×(4/5)^4×(1/5)
これらをすべて足すと8660/(5^6)=0.554…
複数を○と判断した場合にどうするのかは等確率で選ぶことにしちゃっていいんだろうか
>>280 正解率は常に80%としています
その場合、80%の前提を覆してしまうので想定していません
>>281 学がないので計算式はよく理解できませんが、55%というのには感覚的には納得できる数字です!
ありがとうございます!
よければこの55%を70%や80%にするために、元の一問一答の正解率がいくつになれば良いのか(例では80%としていた部分)も教えてもらえないでしょうか?
>>282 やはりそこの定義付けが必要になりますか
ひょっとしたらなくてもいけちゃうのかな?とも思ったのですが、必要でしたら等確率で構いません
最初に2つ○となった場合、そのうちのどちらかを選ぶのは二者択一なのだからその中に正解のaがあるなら80%でaを選ばないとおかしいことにならないか?
じゃあ、3つ○となった場合、その中にaがあったらどうするのかとかちょっと不確定な要素が多いように思う
>>284 あくまでフラットな状態での正解率が80%であって2つ◯がつく=わからない問題である、と捉えた方が実践的なのでわからない問題=等確率でOKです
>>285 それでは二択を8割で合わせれないよ
選択肢2つのケースはどう考えるんだ?
二択を8割で当てられるとしてそれが5問並んでいる
答えを一つが前提にすると5つとも正しいと判定した場合その5個の中からランダムに一つ選ぶ?
全部解なしと判断した時は五択にかける行動をするのか?
選択肢を二者択一で比較検討した時にベターなものを80%で選べて
ダメなもの同士を比較したときはふつうに1/2で選ぶ
特定の二択につき一回しか比較不可能
っていうルール下で
どういうセレクションが1番正答率高く出て何パーなのか
みたいなのなら考えれるのでは?
>>283 複数○が付いた場合の行動を
>>281のように定義して良いのであれば
各選択肢の○×を正しく判定する確率がxのとき、正しい選択肢を解答できる確率はx(2x^3+x^2+x+1)/5
あとはwolframとかで近似解計算してくれ
>>286 わからない=等確率
で良い、と判断したので
アンパンマンはパンである→2択を選ぶ→結果80%
アンパンマンはパンである
カレーパンマンはラーメンである
両方◯と判断した場合=わからない=等確率という仮定です
>>287 >>289 その通りです
五角形の鉛筆転がします
仮に4択までは絞れるなら1/4にしたいところですが
>>291 walframですか
ぐぐってみます
前提は◯2つ以上で等確率という計算ですよね
それで大丈夫です
ありがとうございました
二択なら8割正解出来る人が、○2つのときそこに正解があるとしても等確率って設定にどうも納得出来ないわ
全然実践的じゃないように思う
そもそもどんな問題でも二択なら正解率80%って設定が実践的じゃないけど
そういう設定をするならすでに答えを知っているが4/5で当たるくじを引いて当たりだったらそのまま正解を答え、外れたらわざと不正解するとかじゃないと実現出来ないんじゃないだろうか
でもその場合だと何択であろうと正解率80%になっちゃって面白くもなんともないけど
>>275の設定が現実的な感じがするね
xは0.4になる
1対1の演習を演習題も合わせて全て回答、理解した場合、進研模試の偏差値はどれくらいが期待できますか?
超えないですよ
満点とったことありますけど80ピッタリでしたから
80.0で本当にぴったりだったんで上限設定されてるのかと思ってました
データの分析を習ったことのないいい年こいたジジイなんだろ
高卒でもない限り偏差値なんて知ってるぞまだ中卒の小僧
偏差値の定義くらい知ってますけど
あなたたちと一緒にしないでください?
東大プレとか100越えたことあるけど、進研模試とか平均高すぎて80も取れない気がするんだけど
なんで上限設定なんてものがあると思ったのかが謎だけどな
数学で満点で80越えないなんてかなり珍しいんじゃないか?
他の回の1位がどんなだか見りゃわかることなんじゃ?
分布表とか出ないの?
>>307 そんなことないと思うけどなあ
進研模試って駿台とかと比べたら下の方まで受けるだろう?
それで満点で80以下が当然なら簡単すぎてマーチレベルくらいからもうほとんど差がつかなくなって模試の意味なくなっちゃうじゃん
実際そんなことにはなっていないようだよ

これだと数学満点なら偏差値88くらい

これなかは得点が無いから満点だったらどうだかわからないけど満点でなくても80越え
やっぱ進研模試でも満点で80.0は例外的に簡単だったんだと思う
進研模試の数学ってミスったらバカwwwwwみたいな感じだしな
だから偏差値の定義も頭に入ってないバカな爺なんだろ
それに進研模試が平均高すぎてと書いてるキチガイがいるけど
進研模試はバカ学校も受けるから平均点は3割程度。
調べる能力もない馬鹿はいちいち書き込まんでいい。
なにがバカかというとろくに調べる能力も労力もないウスラバカが
自分の狭いダサい価値観のみが普遍的な事実であるかのように妄想
してるところ。
まじで病院いってこい。
>>312 ある無矛盾な公理系τの任意のモデルに対してある論理式φが常に真となるならば、τからφがLKにおいて証明可能となることを示せ
>>313 >>978 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 00:59:28.70 ID:BoJlALsC [1/20]
>>977 >より進んだ数学の中には、多項式としては 0 ではないが、それを多項式関数と見た場合は 0 というようなものがある。
ありません
複素関数を考えるにしても、多項式、すなわち連結領域上の正則関数を考えるならば、一致の定理よりある部分で0なら全体で0です
多項式とは有限次元で打ち切りですから、収束半径は無限大、すなわち複素数全体で0となります
前スレ
>>979 自分:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:11:11.10 ID:MxKVVcoK [2/4]
>>978 標数2の素体上で多項式関数 x^2+x を考えると、これは常に0関数となります。
前スレ
>>980 返信:132人目の素数さん[sage] 投稿日:2018/10/18(木) 01:13:16.71 ID:BoJlALsC [2/20]
>>979 殺す
仮に同じとして差を取って微分すれば常に0になる
二つのグラフの差は定数
>>316 不連続のある関数なら定数は連続区間ごとに変えていいぞ
↑化け物がドアップで出てきてギャーーーーーって叫ぶ動画
>>559 4+7=11じゃなくて
Ω={(i,j)|1≦i≦4,1≦j≦7}から
#A=(4x7)-(3x6)=28-18=10により
∴Tの要素数の最大値は10
>>607 それだと5,7で1~24のとき最大値12が説明できないのでは?
■スイッチング関数
Table[2n-1+(-1/4+i/4)((-i)^(n-b)+i^((n-b)+1)+(-1-i)),{b,1,4},{n,1,10}]
Table[2n-1+{((n-b)+3)mod4},{b,1,8},{n,1,10}]
二項定理と数列の性質なんですが、
X〔k+m]+Y〔k+m〕√5=(X〔k〕+Y〔k〕√5)(X〔m〕+Y〔m〕√5)
※〔〕は小文字
凄く簡単みたいなんですが、意味がわからないので教えていただけると有難いです
y=(2x+1)^2はy=0のときx=-1/2になりますが、頂点の座標は(-1,0)ですよね?おかしくないですか?
Table[2n-1+{(n-4)+3mod4}+C(1,n-9)((-1)^n+1)/2+C(3,n-8)((-1)^(n+1)+1)/2,{n,1,10}]
{1, 4, 7, 10, 9, 12, 15, 18, 20, 21}
☆☆☆
Table[2n-1+{(n-2)+3mod4}+C(1,n-6)4((-1)^(n+1)+1)/2,{n,1,10}]
{3, 6, 5, 8, 11, 14, 17, 16, 19, 22}
>>616 Table[2n-b+{(n-1)mod4}+4C(0,n-9),{b,0,1},{n,1,10}]
{2, 5, 8, 11, 10, 13, 16, 19, 22, 21}
{1, 4, 7, 10, 9, 12, 15, 18, 21, 20}
1の4乗根て±1と±iですよね。
「4√1(←4×ルート4じゃなくて、√の左に小さい4のあるヤツ)はいくらか?」て書いてあったら
何と答えるのか教えてください。
自分としては「1」だと思いますが間違ってますか?
それで「-4√1」だったら「-1」だと思うんですが?
あと「-4√1」みたいな書き方で「+i」とか「-i」て答えなければいけない書き方てあるんでしょうか?
証明問題で、よって,ゆえに,したがって、といった接続詞を全て∴の記号に置き換えても問題ありませんか?
そもそも 故に 従って とか単に記号に置き換えてもよさそうな所にわざわざ書く必要ないよ
質問系スレッド18あるうち、ここが一番近いと思ったのでお借りします
(万一スレチならすいませんがスルーお願いします)
三点A,B,Cがあり、AB=AC=BCの場合、この図形は二次元の正三角形である
四点A,B,C,Dがあり、AB=AC=AD=BC=BD=CDの場合、この図形は三次元の正四面体である
五点A,B,C,D,Eがあるとする
AB=AC=AD=AE=BC=BD=BE=CD=CE=DE を満たす場合、
その図形は四次元(またはそれ以上)空間の図形になるでしょうか?
もしそのような図形がある場合、各頂点の座標はどうなるでしょうか?
>>624 そうだね 実際必要不可欠だと思う? 無いと意味変わるかな?誤解されるかな?
同値変形であるのかないのかとか 何故その変形が許されるのかとか その手の事に比べたらホントどうでもいい事だと思うよ
次の問題の解き方を教えて下さい。
【問題】
箱Aの中に10円硬貨、50円硬貨、100円硬貨がそれぞれ34枚・30枚・35枚入っています。
これに対し次の操作を繰り返し行う。
操作
2種類の硬貨を1枚ずつ箱Aから取り出し、代わりに先ほど取り出さなかった種類の硬貨2枚を,箱Aに入れる。
たとえば10円硬貨、50円硬貨を1枚ずつ箱Aから取り出したとき、代わりに100円硬貨を2枚箱Aに入れる。
このとき、箱Aの中の硬貨を1種類だけにすることができるか。できるならば、その具体的な手順を説明せよ。
できないならば,そのことを証明せよ。
出来ないような気がするが証明が合ってるかどうかよくわからない
その操作によって2種類の硬化の枚数の差は変わらないか3変わるかどちらか
現在の差は1、4、5なのでどの2種類もその操作を何度繰り返してもその差が0になることはない
最後に1種類だけになるにはそれ以外の2種類を1枚ずつ取り出しその2種類が0になる場合だけだがそうすると2種類の差が0であるときがあったことになり矛盾する
(10円玉の枚数) + (50円玉の枚数)*2 という値(Xとしよう)を考えると
10円が増える操作では変化しない
50円が増える操作では3増える
100円が増える操作では3減る
いずれにせよXを3で割った余りは変化しない
終了状態(いずれかのコインが99枚)でXは3の倍数
初期状態でX=94 は3で割って1余るので不可能.
>>630-631 どうも有り難うございます。
3で割った余り(3の剰余系?)で分類すれば良い訳ですね。
背理法になりますかね。
Table[2n-b-a+{(n+a)mod4}+4C(0,n-8+a),{a,0,1},{b,0,2},{n,1,10}]
{3, 6, 9, 8, 11, 14, 17, 20, 19, 22}
{2, 5, 8, 7, 10, 13, 16, 19, 18, 21}
{1, 4, 7, 6, 9, 12, 15, 18, 17, 20}
{3, 6, 5, 8, 11, 14, 17, 16, 19, 22}
{2, 5, 4, 7, 10, 13, 16, 15, 18, 21}
{1, 4, 3, 6, 9, 12, 15, 14, 17, 20}
高校数学じゃなかったらごめんなさい
n分の1の確率であたるくじをn回ひいていちども当たらない割合をAとすると
A=(n-1 )^n /n^n
ここでn→∞のとき近似値は0.37は有名だけど、Aは計算で展開できますか?
ありがとうございます!電卓たたいたら本当でした、知らなかった➰
えっ知ってて0.37って言ってんじゃないの?
A=(n-1 )^n /n^n=((n-1)/n)^n
=(1-1/n)^n
=(1+1/(-n))^n
=[(1+1/(-n))^(-n)]^(-1)
n→∞で[]の中がeになるから1/e
>>637 知らねーから質問してんだろーが
そして教えてやったら「知らなかった」といって喜んでんだろ
どう超解釈したら「知ってて言ってる」になるんだよ
いっかい精神病院いってこい
別に展開してるわけじゃないし1/eの方が0.37より有名だよ
どこで聞いていいかわかりませんが
高専ではフーリエや線形代数は習いますか?
>>641 習うけど大学でやるのと比べると程度は抑えられている
ふわっとした質問で恐縮なんだけど
関数の最大値最小値を求める数1の問題と
領域を求める数2の問題って似たような感じがするんだけど
違いってあります?
領域に境界が含まれるか否かを確認しなければならないのが最大最小問題の肝かな
ww.sankei.com/premium160627/prm1606270012-a.html
嘘つきマスゴミ障害者ウヨ猿産廃便所紙ゴキブリの人皮を剥がせ
ゴキブリ産廃便所社員を死刑にしろ
(2^(m+1)-2)/m が整数になるような自然数mは
1,2,6 の先にもまだまだありますか。
>>648 無数にある。
n≧0 のとき m=2×3^n はその性質を満たす。
なんと。そうなんですか。
これは簡単に示せるのですか。僕には無理?
1以上22以下の自然数の集合をSとする
Sの部分集合Tで、次の条件を満たすものを考える
[条件] Tに属する任意の2つの要素の差は4でも7でもない
Tの要素数の最大値はいくらか
1 5 9 13 17 21
2 6 10 14 18 22
3 7 11 15 19
4 8 12 16 20
aを定数とする。0≦x≦1のとき、関数y=-4^x+a*2^-x+2の最大値とそのときのxの値を求めよ
2定点A,Bと直線Lが与えられたとき
(例として座標表示でA(-1,0), B(1,0), L:y=x+4 とします。)
AとBを通りLに接する円を定木とコンパスで作図するにはどうすればいいですか。
>>657 AP = (PとLの距離)
を満たす点の軌跡を求めて(放物線) y=x+4 との交点求めればいいんじゃない?
>>659 求めた点は2次方程式の解なんだから作図できるじゃん。
数値的に解いた結果が作図できるというのと
作図的に解くというのは違うのでは?
>>657 直線ABとLの交点をCとおく。
CA・CB=CT^2を満たすTを作図する。
具体的には|CA|,|CB|を直角を挟む直角三角形を作図し、その外接円に内接する正方形を作図し、その一辺の長さaをとり、CT=aとなる点をとる。
△ABTの外接円が求める円。
Tは2つあるので円も2つできる。
質問主657ではないけど
なるほど方べきか
使い方が上手いなあ
本気で感心した
けっこう難しく手がかかるものなのですね
ありがとうぼざいます
すみません。下記の問題の解き方を教えて頂けないでしょうか。
【問題】
正四面体の各頂点をABCD、各頂点から等距離にある中心点をEとする。
中心点Eから各頂点への距離が30cmのとき、以下の問いに答えよ。
① 正四面体ABCDの一辺の長さを求めよ。
② 正四面体ABCDの高さを求めよ。
③ 正四面体ABCDの体積は、四面体BCDEの何倍か答えよ。
頂点座標が(0,0,0),(0,x,x),(x,0,x),(x,x,0)の正四面体を考えると、
一辺の長さ、体積、中心点から頂点への距離は簡単に出せる
前
>>186 >>665 ②中心Eは正四面体ABCDの重心で、4つの頂点からそれぞれ向かいあう面に引いた4つの高さはすべてEで交わる。正三角形の重心が正三角形の3つの高さをそれぞれ2:1に分ける点で交わることから、Eはその3つの高さをそれぞれ3:1にわけるはず。
(たとえばベクトルで表すと→AB/3+→AC/3+→AD/3=→AE=→3AH/4)
∴30(㎝)×(4/3)=40(㎝)
③底面の△BCDが共通で、高さが4倍だから、体積は4倍。
①正四面体ABCDの一辺をxとおくと、面の高さ、たとえば辺BCに対する頂点Aの高さは、BCの中点をMとして、
AM=(√3)x/2
MH=(1/3)MD
=(1/3)AM
=(√3)x/6
△AMHにおいて三平方の定理より、
AM^2=AH^2+MH^2
3x^2/4=40^2+3x^2/36
27x^2-3x^2=1600・36
24x^2=1600・36
x^2=800・3=2400
∴x=20√6(㎝)
以下の問題の答えを教えてください
白、青、緑、赤に塗られたボールが箱にたくさん入っている。
ボールが全部でいくつあるのかは分からないが、
全部の個数に対するそれぞれのボールの割合は
白……58%
青……29%
緑……10%
赤……3%
箱から無作為にボールを1個取り出すのを4回繰り返すが、
1個目のボールを取り出した後箱の中の赤のボールを全て取り除き、
2個目のボールを取り出した後箱の中の緑のボールを全て取り除き、
3個目のボールを取り出した後箱の中の青のボールを全て取り除く。
このとき4回連続で白のボールを引く確率は?
>>673 ボールが整数個であるためには
全部の個数が100nである必要がある
>>674(≒22.69%)はn=1における確率だが
nを大きくしていくと
極限1682/7275(≒23.12%)に漸近していく
というか
>3個目のボールを取り出した後箱の中の青のボールを全て取り除く。
この設定なしで「3回連続で白をひく確率」でいいのでは?
>>674 >>675 ありがとうございます
>「3回連続で白をひく確率」でいいのでは?
それはレスしてから気づきました
>>673前
>>672 lim(x→∞)58(0.58x-1)(0.58x-2)/(0.98x-1)(0.87x-2)
lim(x→∞)(195112x^2-10092x+20000)/(8526x^2-28300x+20000)
微分して(195112・2x-10092)(8526x^2-28300x+20000)-(195112x^2-10092x+20000)(8526・2x-28300)=0
(390224x-10092)(8526x^2-28300x+20000)-(195112x^2-10092x+20000)(17052x-28300)=0
(97556x-2523)(8526x^2-28300x+20000)-(195112x^2-10092x+20000)(4263x-775)=0
4回連続白が出る確率を考える。
1回目は0.58x個あった白が
2回目には(0.58x-1)個、
3回目には(0.58x-2)個と減っていて、
4回目をとるときは、
(0.58x-3)個ある。
全体の個数は、
2回目には赤3%を除き、97%になる。
3回目には赤3%と緑10%の合計13%を除き、87%になる。
4回目には赤3%と緑10%と青29%の合計42%を除き、58%になる。
つまり(0.58x-3)個、
これは白の数と同じ。
4回目は100%白が出る。
x=100のとき、
58・57・56/96・87=133/6
=22.166……
x=200のとき、
58・115・57/193・86=29・115・57/193・43
=190095/8299
=22.905771……
x=300のとき、
58・174・173/290・259=174・173/5・259
=30102/1295
=23.244787……
前
>>677訂正。
1も2も全体の数xと比べてじゅうぶん小さいから、
(58^3/97・87)・100
=58^2・200/97・3
=11600/291
=23.120274……
前
>>678修正。
=58^2・200/97・3
=58・11600/291
=(58000+5800+34800)/291
=(63800+34800)/291
=98600/291
=23.120274……
e (ネイピア数) = 2.71828,,,, と言うのがありますよね。極限の式
(1 + 1/n)^n
lim n → ∞
で、得られる数値ですが、これの n を x に置き換えた指数関数として y = (1 + 1/x)^x を考えます。
先の極限の式は有名なので、y = もよく扱われているだろう。と思っていました。
そこで、グラフで見たいと思いネットで探しました。しかし、指数、対数の一般的な
グラフはあるのですが、ピッタリのグラフは見当たりません。
そこでお願いです。
y = (1 + 1/x)^x のグラフのあるサイトを教えて下さい。
または、この式のグラフが描けるツールを教えて下さい。
一応、ツールも簡単ですが探しましたが、一般的な指数、対数のグラフ用で
求める式のグラフ作図は出来ない印象を受けました。
n つまり x は 1-20 程度を考えています。
宜しくおねがいします。
レス:1-200 201-400 401-600 601-800 801-1000 ALL
このスレへの固定リンク: http://5chb.net/r/math/1548693213/
ヒント:5chスレのurlに http://xxxx.5chb.net/xxxx のようにbを入れるだけでここでスレ保存、閲覧できます。
TOPへ TOPへ
全掲示板一覧 この掲示板へ 人気スレ |
>50
>100
>200
>300
>500
>1000枚
新着画像
↓「高校数学の質問スレPart399 YouTube動画>1本 ->画像>13枚 」を見た人も見ています:
・ソフィーのアトリエ 攻略質問スレ Part3
・【投資一般板】 初心者質問スレッド Part64
・【ごまおつ】ゴシックは魔法乙女 質問スレ★51【初心者歓迎】
・新規スレッド立てるまでも無い質問@車板501
・スレ立てるほどもない質問に嘘八百で答えろ46
・MHWの質問に全力で答えるスレ122
・欅坂46の長濱ねると面識あるけど質問ある?
・子宮内でずっと不登校してるんだが質問あるか?
・【仙台高裁】大川小訴訟 「津波と無関係な学校ではありませんよね」 裁判官の質問で原告が涙★6
・都内で家賃4万円の部屋住んでるけど質問ある?
・部活3ヶ月で辞めたけど質問ある?
・偏差値47の高校から筑波理工受かったけど質問ある?
・【テレビ】『めざまし8』再炎上! 谷原章介“土石流被災者”に不謹慎質問「残念な人」 [jinjin★]
・【これがバカマンコだ】 「相手が自分に気があるかどうか」 必ずわかるという必殺技の質問がこちらw
・オフ大会総合スレPart.58 ※転載厳禁
・【BiSH EMPiRE】wack総合スレッド part82【BiS GANG PARADE】
・【覇権候補🐰】未来の覇権を探すスレ シノアリスpart631【スマゲ支部🏡】
・TUBEスレッド Part164〜 🐖🐗💩🚽
・【DQW】ドラクエウォーク 無課金スレ part.63【コテハン禁止】
・iOS 15.xを語るスレ Part16 ★
・前田彩佳ちゃんが難関大学の受験にチャレンジする模様
・豊島将之 Part69
・【邪神ちゃんドロップキック】ぺこらはホームレスかわいい Part9
・カントク part10
・熊本大学part23
・アンテナケーブル分配器分波器ブースター Part22
・【リーフ】FR・LGの女主人公に萌えるスレ 39
・【齊藤陽介】十字珍宝オンラインPart9153【後藤美名子】
・【鯵】アジングを楽しむ part91【ルアー】
・Pにゃんこ大戦争~多様性のネコ~Part3【京楽】
・【グラクロ】七つの大罪 ~ 光と闇の交戦(ひかりとやみのグランドクロス) part137
・【クリユニ】クリスタルオブリユニオンpart73
・スポットバイトル part1
・東北高校PART34
・東北高校PART37
・【AM4】AMD Ryzen 9/7/5/3 Part317
・誉高校 part2
・東北高校PART35
・東北高校PART36
・【DMM.R18】あやかしランブル!part111 ©bbspink.com
・高校アーチェリーpart3
・【MGSV】METAL GEAR SOLID V part520【GZ/TPP】
・【健康】太奥、元太奥のダイエット【痩せる】 Part.6
・NMB48本スレ★10239
・【五輪】東京五輪ロゴの白紙撤回を求めるデモスレ2
・オッツダルヴァと書くと良い事が起きるスレ
・AMD雑談スレ 981条
・℃-uteのブログとInstagram更新を辛抱強く待つスレ 952待ち
・Nintendo Switch総合スレ★874
・青山学院大学陸上競技部応援スレ97
・◆◆◆雑談専用スレ★411◆◆◆
・Shadowverseまったりスレ 428ターン目 【シャドウバース】
・新潟市都市開発スレ140
・☆☆☆ 俺の塩総合スレ 3 ☆☆☆
・闇金情報スレ 238
・【地獄先生ぬ~べ~及び霊媒師いずな】葉月いずなスレ
・【悲報】松村沙友理の卒業2スレもいかず終わり
・【櫻坂46】小池美波応援スレ★21【みいちゃん】
・コーヒーや紅茶を飲みながらのんびり屋の1と話すスレ
・NHK総合を常に実況し続けるスレ 183425 おパンツ
・◆視聴率情報提供専用スレ3512◆
・【つまハゲ】レプリカを語るスレ【ヒカゴ】 ★2
・【UFC】海外MMA総合スレ その891【Bellator】
・IIDXランカースレ(IDなし)★171
・ロリータ画像総合スレ
・【般若】写経スレ【心経】 #02
00:56:28 up 103 days, 1:55, 0 users, load average: 23.72, 21.06, 18.83
in 0.016247034072876 sec
@0.016247034072876@0b7 on 072913
|







 これだと数学満点なら偏差値88くらい
これだと数学満点なら偏差値88くらい  これなかは得点が無いから満点だったらどうだかわからないけど満点でなくても80越え
これなかは得点が無いから満点だったらどうだかわからないけど満点でなくても80越え 


 これだと数学満点なら偏差値88くらい
これだと数学満点なら偏差値88くらい  これなかは得点が無いから満点だったらどうだかわからないけど満点でなくても80越え
これなかは得点が無いから満点だったらどうだかわからないけど満点でなくても80越え