�����w���̐��w��D�����N�����I
�Ȃ�тɏ����w�Z�͈͂̎Z���E���w�̖��ŔY��ł�����I(�N����킸)
������Ȃ���肪��������C�y�Ƀ��X���Ă��������B
�w�Z�̏h��A�m�̖��ȂǕ��L�������Ă��������Ǝv���܂��B
�����̎g��������>>2���Q�Ƃ̂��ƁB
�������܂ŏ����w���̂��߂̃X���Ȃ̂Ŕ͈͊O�̂��̂ɂ��Ă͕ʃX���ɁB
���炩�ɔ͈͊O�̎���ɂ͑�NG�o�^�őΏ����Ă������B���������畉���ł��B�F�l�̂����͂�낵�����肢���܂��B
�O�X��
�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 58
http://2chb.net/r/math/1642258588/ >>3

> calc(43,51,13,17)
deg
1 26
26���ł����Ă�B �O>>3
>>4���肪�ƁB
����ς菬���w�Z�͊�����ˁB �����w�����^�����Ċ��ŏ����悤�ɂȂ�����L�Q�ł���
�O>>5
AP��BP��CP�̕ӂ̔䂪�{�p�O�{�p�ŕ\����B
��BAC=56����26����30���ɕ����邵���Ȃ��B
����BAP=26�� ���ꋳ����
447�P�R�Q�l�ڂ̑f������2022/04/03(��) 20:57:44.19ID:zdgXgqlk>>452
�L�����Ȃ̂Œm���Ă�l�͂����������Ă���B
�S�v�f�̘a��2022�ƂȂ�2�ȏ�̎��R���̏W�����l����B
���̂悤�ȏW���̑S�v�f�̐ς̍ő�l�͂������H
��) ����2022��10�̏ꍇ�ɂ��āA�ȉ��̒ʂ�ɉ������B
�u�S�v�f�̘a��10�ɂȂ�2�ȏ�̎��R���̏W���̑S�v�f�̐ς̍ő�l�͂������H�v
�S�v�f�̘a��10�̏W���ƁA���̎��̐ς͈ȉ��̒ʂ�B
�W���F�i10�j�A�ρF10
�W���F�i2,8�j�A�ρF2*8=16
�W���F�i3,7�j�A�ρF3*7=21
�W���F�i4,6�j�A�ρF4*6=24
�W���F�i5,5�j�A�ρF5*5=25
�W���F�i2,2,6�j�A�ρF2*2*6=24
�W���F�i2,3,5�j�A�ρF2*3*5=30
�W���F�i2,4,4�j�A�ρF2*4*4=32
�W���F�i3,3,4�j�A�ρF3*3*4=36
�W���F�i2,2,2,4�j�A�ρF2*2*2*4=32
�W���F�i2,2,3,3�j�A�ρF2*2*3*3=36
�W���F�i2,2,2,2,2�j�A�ρF2*2*2*2*2=32
���̒��Őς̒l���ł��傫���̂́A36�B
���̂��߁A2022�̕�����10�ɕς����ꍇ�̉�36�B �p�b�g��3�����������ǂ�����
>>8
5�ȏ�̗v�fa�������a��a-2,2�Ǝ�芷����Θa�͕ς�炸�ς͑����邩��5�ȏ�̗v�f�͂Ȃ�
4���Q�����4,4��3,3,2�Őς������邩��4�͂ЂƂȉ�
2���R��L���2,2,2��3,3�ő����邩��2�͂Q�ȉ�
2��4���L���2,4��3,3���_��
�܂Ƃ߂��
�E2��2�ȉ�
�E4��1�ȉ�
�E2,4�����g���̂̓_��
�E�c���3
���K�v����
�����������̂͑S��3�����Ȃ� a[1]�Aa[2]�A�E�E�E�Aa[n]�͂ǂ̍������Řa��A�ł���Ƃ���
�������敽�ςɂ��(A/n)^n����[k=1,n]a[k]
���ӂ̑ΐ�������n(logA-logn)�@��������Ɓ@logA-logn-1
n��1����A/2�܂œ����̂�n=A/e�̂Ƃ��ő�ƂȂ�
�䂦��a[1]�Aa[2]�A�E�E�E�Aa[n]�̂ǂ����e�ɋ߂��Ƃ��ς��ő�ɂȂ�
�܂�2�܂���3�̐ςɂ��Ă̂ݍl�����邾���ł���
A=2022�̏ꍇ��674*3�Ȃ̂őS��3����Ȃ��3^674���l����
������3��2��菜��2��3������Ƃ��̉ӏ���2^3/3^2=8/9�Ō�������
�䂦�ɑS��3����Ȃ��3^674���ő�
�O>>7
�����w���ɂ͏K���Ă��Ȃ��Ƃ��߂Ƃ��������Ȃ��ւ��肪����B
������Ŋ��͍őP�̕��@���B
��BAP=26���̂Ƃ��A
��BAC=��ABC=180��-(13��+43��)-(51��+17��)
=56��������BC=AC
��CAP=56��-26��=30��
��ACP�ɂ�����AC/sin47��=AP/sin17��=PC/sin30��
=2PC
AC=2PCsin47��
��BCP�ɂ�����BC/sin86��=BP/sin51��=PC/sin43��
=BC/2sin43��cos43��
BC=2PCcos43��
�������ꂽ�B >>12
���������ɂȂ�悤�ɖ����쐬����̂������ȁB
���̃g���[�j���O�@�Q��


�����ł��炠�Ƃ��痝�����l����
�Տ��������Ă���Ȋ����B������ȂǍזE�E���q���x���ł̗����͂��ƕt���B �A�r�W�W�C�̔]���Տ��ł͂����Ȃ��Ă�́Hw
�ォ�痝�����l����wwwww
���O�ɂł��邩�A�z�`wwwwwwwwwww
�O>>12
>>13
24��(��BAP=2��CAP�Ƃ���Ɩ������݂���Ȃ�)
60��(2��PBC=��PCB�������BAP=2��ACP�Ȃ�o�����X������) �O>>16�����B
>>13
24��(��BAP=2��CAP�Ƃ���Ɩ������݂���Ȃ�)
52��(AP���߂��ĂĒ����������ɃM�U���Ă邩��60���͂Ȃ��B��BAP=98�����ǂ������邩�B
52����46���ɕ�����Ɩ������݂���Ȃ�) x�͐����B�f��p�� (x^2)+1 �������Ƃ�
p��4�Ŋ��������܂��3�ł͂Ȃ����Ƃ�����
𝔽ₚ�̏�@�QG�ɂ����ē�悷��ʑ���f�A(p-1)/2�悷��ʑ���g�Ƃ����im(f) = ker(g)
�����
-1�̗ނ�������
�� -1 ��im(f)
�� -1��ker(g)
�� (-1)^((p-1)/2) �� 1 ( mod p ) or p = 2
�� p �� 1 ( mod 4 ) or p = 2
�O>>17�Տ������B
>>13
(���})
��BAC=180��-(54��+42��)-(30��+18��)=36��
��BAP=24��,��CAP=12���Ƃ���ƁA
��APB=180��-(24��+54��)=102��
��BPC=180��-(42��+30��)=108��
��CPA=180��-(18��+12��)=150��
��APB+��BPC+��CPA=102��+108��+150��=360��
����BAP=24��
—————————————————————
(�E�})
��BAC=180��-(19��+11��)-(22��+30��)=98��
AP���߂��Ă邩���BAP��60��
��BAP=52��,�� CAP=46���Ƃ���ƁA
��APB=180��-(52��+19��)=109��
��BPC=180��-(11��+22��)=147��
��CPA=180��-(30��+46��)=104��
��APB+��BPC+��CPA=109��+147��+104��=360��
����BAP=52�� x^2+1=4m+3�Ə�����Ƃ���Ɓ@
x^2=4m+2
�E�ӂ������Ȃ̂ō��ӂ������ƂȂ�x�͋���
�䂦�ɍ��ӂ�4�̔{���ƂȂ邪�E�ӂ͂����łȂ����疵��
a>0, b>0, c>0, d>0
a*b*c*d=1�����Ƃ�
a+b+c+d��4
�������B�i���w���x���łȁj
a + b - 2��ab = (��a - ��b)²��0 �� a+b �� 2��ab
c + d - 2��cd = (��c - ��d)²��0 �� c+d �� 2��cd
2��ab + 2��cd - 4���abcd = (2��ab - 2��cd)²��0 �� 2��ab + 2��cd �� 4���abcd
�� a+b+c+d �� 4���abcd
>>15
�C���t���G���U�̌o�@���N�`���ƒ��˃��N�`�����ׂ�Ɨ��_�I�ɂ͕���^�R�̂�U������o�@���N�`���̂ق������ʂ������Ƃ����\���͗Տ������Ŕے肳�ꂽ�B
�㗝�G���h�|�C���g�ł̔�r�������Տ��Ƙ�������̂͂����Όo������BCAST�����Ƃ��Ō�t�ł��m���Ă���B �}���V�����ɕی��K���̂���Z�t�@�����`���Ƃ��A�F���ꂽ�_���ɂ�����ƍ����͓��v�I�ɂ��ɂ߂Ĕ���B
��p�@���ȂǑS���s���B
>>25
�܂����O�ɂ͂��������������Ă�̂����痝���o���ĂȂ��� >>24
�����B�B�Ƃ������A�f�ł��̏ؖ����ӎ����甲���Ă���
���܂�
���w���x�����ƋA�[�@������ĂȂ�����A���̂��炢�����E���ȁB �O>>20
>>13
(�E�})
AP�̉�������BC�̌�_��Q�Ƃ���ƁA
��ABQ�䁢CBA(��2�p��������)
��BQA+��PBQ=11��+98��=109��=��APB
��������52���ł����Ă�Ǝv���B
���}��2�{�p��3�{�p�ɂȂ�24���������Ƃ��炵���A
������\��������B �O>>29
BP�̉�������AC���������邩��A
APsin12��=CPsin18��
������ǂ������A�Ƃ�������B �U�N���̔�̗��p���ŗ������m�肽���ł�
��@A��2/5��B��3/4�����������A
A��B�̔���ł��ȒP�Ȑ����̔�ŕ\��
����8:15�Ƌt�ɂȂ��Ă��܂��܂�
��낵�����˂������܂�
�O>>30
>>31
��ӂ��(2/5)A=(3/4)B
8A=15B
��A:B=15:8 >>31
A��2/5��C�Ƃ����B��3/4��C
A��C��5/2�{�ŁAB��C��4/3�{
�܂�AC:A:B=1:5/2:4/3������A:B=5/2:4/3
�ȒP�Ȑ�����ɒ����ɂ͗���6�{����15:8
�����ǂ��Ԉ���Ă���̂��͖����ǂ������v�Z�������̂������Ȃ��Ɠ����悤���Ȃ� >>32���� >>33����
���肪�Ƃ��������܂�
A��C��5/2�d�̐����ŗ����ł��܂���!
���肪�Ƃ��������܂��� �O>>32
������̓��̒��ɏZ��ł��邨������̕�����2/5�ƁA
�s�G����3/4�����傤�Ǔ������ƍl������������Ȃ��ł��ˁB
�������搶�Ȃ�A����Ȃ��킢�炵�����E�͕������ɁA
���ɂ���Ƃ���Ɏ��𗧂ĂȂ����܂������Č����Ǝv���܂��B
�܂��ł��A��l�����̂���ȐS�z�Ȃǂ��悻�ɂ����ɑ傫���Ȃ��ł��傤�ˁB >>20
��}���Ă̗Տ�����
> calc(42,30,54,18)
A = -0.132157+1.257387i
P = 0.3906944+0.3517828i
deg
24
> calc(11,22,19,30)
A = 0.689144+0.3978775i
P = 0.6751701+0.1312398i
deg
57 �O>>35
>>20
����Ȃ��ȁB
��BAP��60���Ƃ��āA
��������52���͂�����Ə������C�������B
53������59���܂�7�ʂ�̓���������̂ɁA
�Ȃ��57���Ȃ낤�H
�`�F�o�̒藝�A���l���E�X�̒藝�A
�����藝��g�ݍ��킹��Έ�ӂɌ��܂�̂����B �A���������������Č�_�̍��W���v�Z�A�x�N�g���̓��ςƋt�]�����g���Ċp�x���v�Z
������v���O�����ɂ����������B
��������̂�萮���ɂȂ���̍쐬�͗������������đI���B
�ɂԂ��ɂ͂��傤�ǂ悩�����B
���̈Ӗ���������Ί��ł��낤���듚�ł��낤���A�����o���Ȃ��ł͂����Ȃ��C�i���ɂ͒E�X�B
���������呲����B�@�s���Ȃ��Ă悩�����B
���͓���Z����̎�����A����ƍ�����w���̓�Z���ł����B
���̂���̕������x�Ƃ��Ă͂悩������Ȃ����ȁB
>>37
>53������59���܂�7�ʂ�̓���������̂ɁA
�v���O�����ł̊ۂߌ덷�Ŏ��͐������ł͂Ȃ��\����������A����������������Ă��Ƃ͂Ȃ���B >>40
�����Ŋw��̈���������w�ɍ��i����Ƃ����̂��e�Ƃ̈Öق̗����������Ȃ��B
���w�̋��t����͊w��̈������������Z�ɍ��i����̂���Ԃ̐e���s���ƌ���ꂽ�̂����ł��o���Ă���B
���̈�������ނ̒n�����Ǝ������Z�͌����ɕs���i�̗������ڂꂪ�d���Ȃ��ɂ������Z�Ƃ����ʒu�Â��������B ���̈�������ނ̒n�����Ǝ������Z�͌����ɕs���i�̗������ڂꂪ�d���Ȃ��ɂ������Z�Ƃ����ʒu�Â��������B
��
���̈��������̒n�����Ǝ������Z�͌����ɕs���i�̗������ڂꂪ�d���Ȃ��ɂ������Z�Ƃ����ʒu�Â��������B
�e�䂳�t�̉A�ŋ����Ă����邾�낤�Ȃ�
���C�̓ł�
>>42
�����S���I�ɂ�������
��������Ȃ��n�������邯�Ǘ�O�I >>40
�����A�r�W�W�C
����ȂƂ���Ŗ������ĂȂ��ł������Ƌ����w�̖��O������ >>40
����Z�̍��Ɉ�w���}���Z�[���Ă�ƕ��͂���ۂǂƂ����v����� �O>>37
��₪���������ėՏ������Ɏ��Ԃ��������Ă邯�ǁA
��₪�������邾���ł�����ƌv�Z����Έ�ӂɌ��܂�͂��B �ʔ������l������(1)�͗U��
(1) (x+y)(x^2-xy+y^2)��W�J����
(2) 3857143��f������������
�N��30���~�҂����l�o��TikToker�B17�ŃX�^�oCEO�̔N������
�Čo�ώ��t�H�[�u�X�ɂ��ƁATikTok�i�e�B�b�N�g�b�N�j��2021�N�ɍł��҂���
�C���t���G���T�[�uTikToker�i�e�B�b�N�g�b�J�[�j�v�̔N����1750���h���i��20���~�j
�ŁA�X�^�[�o�b�N�X��A�N�Z���`���A��CEO�̔N���������Ă����B
�t�H�[�u�X�����\�����u2021�N�ɍł��҂����e�B�b�N�g�b�J�[�v�����L���O��
���2�ʂ�Ɛ肵���̂́A�f�B�N�V�[�E�_�~���I�iDixie D�fAmelio�j�ƃ`���[���[�E
�_�~���I�iCharli D�fAmelio�j�̎o���������B
1�ʂ͖��̃`���[���[�E�_�~���I�ŁA�N����1750���h���B2004�N���܂��
�`���[���[��21�N���_��17�A�t�H�����[����1��3400���l���ւ�B���ϕi���[�J�[
�ȂǂƂ̍L���X�|���T�[�_��ɉ����A�o�̃f�B�N�V�[�Ƌ��Ƀt�@�b�V�����u�����h��
�����グ���ق��A�e���r�ԑg�ɂ��o�����Ă���B
2�ʂ͎o�̃f�B�N�V�[�E�_�~���I�ŁA�N����1000���h���i��11��5000���~�j�B
21�N���_�̔N���20�ŁA�t�H�����[���͖�5700���l�B
�Ŕ���193�~�̏��i��24�������Ƃ�����A���v�̐ō��݉��i�Ɛō��ݒP��������ɂȂ�H
���̐ݒ肾�ƒ[�����o��
�[���̈����͎��Ǝ҂����߂���̂ň�ӂɓ����͏o�Ȃ�
>>53
�ł͐ō��ݒP����213�̍��v5095�̏ꍇ���Ăǂ������������藧���Ă܂����H
����213�ɂȂ�̂�������Ȃ��� �{�̒P��213�~�̏��i��n�����ꍇ
���Ǝ҂�1�ԂԂ�ǂ낤�Ǝv����21.3�~�̒[����グ��22�~�A�P���ō�235�~�ɂ���n�̒l�i��235n�~
�ł��ǐS�I�Ȃ̂͐�̂ĂĐō��P��234�~��n�̒l�i��234n�~
���͈̔͂ŏ���Ɍ��߂Ă�����Ȃ��́H
�O�O���Ă����Ǝ҂����߂Ă����Ƃ����o�Ă��Ȃ�����m���
���肪�Ƃ��������܂��B
�����_�ȉ���������グ��Ǝ҂����āA����͔C�ӂŌ��߂�����Ă��Ƃł��ˁB
����łɂ��Ă��Z���ɂ��Ă��S���킩��Ȃ��̂ŕ��ɂȂ�܂����B
���߂�A����ϑ���̃~�X��������
212�ł����B
�Ȃ��������ȂƎv������
���߂�̖��̐����������Ăق�������
�u1��240�~�̃�������1��160�~�̃I�����W��S����12�����3,000�~�x��������760�~�̂��ނ肪�߂��Ă�����I�����W�������͂������H�v
���Ė��
3,000�~�x�����Ă��ނ肪760�~������
���v2,240�~
2400���i240+160X�j�~12�@�Ȃ̂��ȁH
�悭�킩��Ȃ��̂ŋ����Ă�����
>>60
���ԈႦ��
2260���i240+160X�j�~�P�Q�Ȃ̂��ȁH 240(12-x)+160x=2240.
2880-80x=2240.
80x=640.
x=8.
4n+3�in�͐����j�Ƃ����`�ŕ\���ł���f���͖����ɑ��݂��邱�Ƃ�����
>>64
+3���Ə����I�ȉ�@�Ȃ���Ȃ��́H
�ꉞ�Z���o�[�O�̏ؖ��Ƃ����邯�� �����A����Ȏ��Ȃ���
�L�������Ȃ��Ƃ��đS��������1�����͂����̂�
�ߎ��l�ƗL�������ɂ��Ă̎���ł�
2�n�_�Ԃ̋����𑪒肵�A10m�������l�̌ܓ����đ���l2700m���B
(1)�L���������Ȃ����B
(2)�^�̒l����m�Ƃ���Ƃ��A���̒l�͈̔͂�s�������g���ĕ\���Ȃ����B
�Ƃ����₢�ŁA(1)��2�Ɠ������Ƃ���A������2,7,0�ł���
(2)�̓�����2695������2705�ɂȂ邽�߁A�M���ł��鐔����2����(�S�A�\�̈ʂ͕K��7��0�ɂȂ�m�͂Ȃ�)�Ǝv���A(1)��2�Ɠ������̂ł����A����7��0���L�������ɂȂ�̂ł��傤��
����������茈�߂Ȃ�ł���H
��������2700.0456....
0.04�ȉ���̂Ă�
2700.0
�ł����A�L�������͍ŏ���2�������Ă킯�Ȃ�
������������Ȃ̖��Ƃ���
2.70�~10³
�̌`�ŏ����ĂȂ��Ə��Ȃ��Ƃ�
2.700�~10³
�Ƌ�ʂł��Ȃ��A�v�Z���Ă��܂�����ǂ�����2700����
���̌`�ŗL������������Ȃ�Ă������������Q�[
���̎���ł͏K��Ȃ������̂ō������ƒ��ׂĂ݂��B
2.70�~10^3
������2,7,0�@�Ȃ̂��ȁB
���������l���Ă݂��B
10m�������l�̌ܓ����đ���l2700m
����
�L������3����
�ɂȂ邩��2.70�~10^3
�����������Ƃ��ȁB
>>72
�����A���������_�\�����Ȃ��Ƃ킩��Ȃ�
2.7�~10³
2.70�~10³
2.700�~10³
...
�S���L�������͈Ⴄ�A���̌`�ŗ^�����ĂȂ��Ɠ����o����͂��Ȃ�
2700�̗L�������́H�Ƃ��Ȃɂ�����Ęb >>69
�����������Ă�낤���ǁA���\�ȗ����Ă�Ȃ� >>75
�킩��z�ɂ̓R���ł킩�邵�킩���z�͂����Ə����Ă��킩�����킩��z�ɂ͖��߂���s�Ԃ͏����Ȃ��̂��d�v�ȋZ�p >>77
�킩��킩����0/100
�����킩��Ƃ����肦�Ȃ�
0/100�v�l�͉��������_������0/100�̃A�z �f���藝�������Ŏv��������A���[�N���b�h���݂̓V�ˁB
�m���Ă��邩�m��Ȃ����̈Ⴂ�ł����Ȃ��B
�Ƃ���ŁA��悷��K�v����̂��H
�ǂ����A�Q���|�邩��A�����Ȃ�Q�ŁA��Ȃ�]�Q�ł���H
�P�����ƂR���]�P������A�ǂ����ł���������ˁH
���̒��x�̗���x�ł��������Ă���A�z
>>71-74
���X���肪�Ƃ��������܂�
�w����10���h�����̖�肾������ł����A
���̃h�����A��b���e���Ώۂ̂��߂�
�ɉ�������ĂȂ��ӏ��������āA
����ł�����܂ł͑��}�̂Œ��ׂĂ���Ă���ł���
����̂͂ǂ����Ă�����܂���ł���
�i�L�������ɂ��ăO�O��Ƃقځu�M���ł��鐔���v�Ƃ�������A
���Ƃ�>>74�̗l�ɏ���✕10�ׂ̂���̏���������ō���̖��̉������ƌ��ѕt�����Ȃ������j
���炭>>73�̒ʂ�ȂƎv���܂����A
���ɂ��Ă̓����������܂��� �X���`���݂܂���B
���w���̎Z���v�����g������ł���T�C�g�Ȃ��ł����H
���тނ��h�����͌Œ�Ȃ̂Œ���I�ɖ�肪�X�V�����悤�ȃT�C�g����������ĉ������B
�O>>49
>>60
x���g���Ă͂����Ȃ��ꍇ�A
3000-760=2240
��������A���ꂳ��A�q������l�A
��������4�Ƃ���ƁA
240�~4=960
2240-960=1280
1280��160=8
��8�� ������ĒߋT�Z���ȁH
240�{�̑��̃��������J�f��160�{�̑��̃I�����W���J�f�����킹��12�C
���̑�����2240
>>86
12-(2240-160*12)/(240-160) ���肢���܂��B
���u�`�N�A�a�N�A�b�N�A�c�N�A�d�N�A�e�N�̂U�l�����܂��B���̎q��������l��g�̃y�A������ĂR�`�[���Ő킢�܂��B
�`�[�������͉��ʂ�ɂȂ�ł��傤�H�v
�Ƃ�����肪�����āA�u�`�a�y�A�A�`�b�y�A�A�`�c�y�A�c�c�Ƃ����悤�Ƀy�A�����ʂ肩���肦�邩�v�Ƃ������ƂȂ̂�
�u�`�a�y�A�u�r�b�c�y�A�u�r�d�e�y�A���P�g�ƍl���āA���̂悤�ȑg���������ʂ肠�肦�邩�v�Ƃ������ƂȂ̂����f�ł���
���w�̖��Ȃ̂ɕ��������B�����Ȃ��Ǝv�����̂ł����A
�ӂƁA�u�Ⴄ�I����́A�ǂ���̉��߂ł������͓����Ȃ̂ł͂Ȃ����v�Ƃ����C�ɂȂ��Ă��܂����B
�����ŁA�ǂ���̉��߂ł��S�p�^�[���������o���Ă݂���P�T�ʂ肾�����̂ł����A�����Ă܂��ł��傤���H
�܂��A�{���͂ǂ������v�Z�ōl����ׂ��Ȃ̂ł��傤���H
C(6,2)*C(4,2)*C(2,2)/3! = 15�ʂ�
>>89
���p���
�q�����W�l�����܂��B���̎q��������l��g�̃y�A������ĂS�`�[���Ő킢�܂��B�`�[�������͉��ʂ�ɂȂ�ł��傤�H
C(8,2)*C(6,2)*C(4,2)*C(2,2)/4!=105 ���p���
�q����9�l�����܂��B���̎q������3�l��g�̃y�A�������3�`�[���Ő킢�܂��B�`�[�������͉��ʂ�ɂȂ�ł��傤�H
3�l���ƃy�A����Ȃ���
����
���p���
�q����9�l�����܂��B���̎q������3�l��g�̃`�[���������3�`�[���Ő킢�܂��B�`�[�������͉��ʂ�ɂȂ�ł��傤�H
�O>>84
>>92
(9C3)(6C3)=(9�E8�E7)/(3�E2)=3�E4�E7=84
��84�ʂ� >>88
�u3�`�[���Ő키�B�`�[�������͉��ʂ肩�B�v�Ȃ̂�������
1�`�[���������Ȃ����Ƃ��u�`�[�������v�Ƃ͌���Ȃ�
�B���ł͂Ȃ��Ǝv��
�O�҂ƌ�҂����ʓI�ɓ������ɂȂ�̂͂��܂���
8�l����1�`�[����I�ԏꍇ��4�`�[�����ꍇ�Ȃǂł͈���Ă��� >>88
�܂�A�ƃy�A�ɂȂ�l�̑I�ѕ���C[5,1] = 5�ʂ�
�c��4�l�̂���1�ԃA�t�t�@�x�b�g���ŎႢ�l��I�т��̐l�ƃy�A�ɂȂ�l�̑I�ѕ���C[3,1] = 3�ʂ�
�� 5�~3 = 15�ʂ�
����{���ŏ������W�����
6!/(2!2!2!)��3! = 15
���X >>88
����ق�����������B
�v���O������g��Ōn���I�ɗB
1 : AB CD EF
2 : AB CE DF
3 : AB CF DE
4 : AC BD EF
5 : AC BE DF
6 : AC BF DE
7 : AD BC EF
8 : AD BE CF
9 : AD BF CE
10 : AE BC DF
11 : AE BD CF
12 : AE BF CD
13 : AF BC DE
14 : AF BD CE
15 : AF BE CD >>93
9C3�@* 6C3 / 3! = 280����Ȃ��H �������
���w���I�ɂ�6�~6�̑�������\����čl���������ǂ���ˁB
���Ԃ�����[�̔�����15�ɂȂ�͂��B
>>92
�q�����P~�X�܂ł̔ԍ������āA3�l����3�`�[���ɂ킯��g�ݍ��킹���
[1,] 123 456 789
[2,] 123 457 689
[3,] 123 458 679
[4,] 123 459 678
[5,] 123 467 589
[6,] 123 468 579
[7,] 123 469 578
[8,] 123 478 569
[9,] 123 479 568
[10,] 123 489 567
....
....
[271,] 189 234 567
[272,] 189 235 467
[273,] 189 236 457
[274,] 189 237 456
[275,] 189 245 367
[276,] 189 246 357
[277,] 189 247 356
[278,] 189 256 347
[279,] 189 257 346
[280,] 189 267 345
280�ʂ� �����ȉ��̌v�Z�����Ȃ̂�
7��35�~�i-25�j�݂����Ȗ�肪����
�A�X�y���Đ��w�͓��ӂȂ�������ĕ���������
�v�Z�����ُ�ɑ����Đ��m�������͖��͑S���o���Ȃ�����
������ƌv�Z�̎d�����킩��Ȃ��̂ŋ����Ă������������ł��D
9=a�ゔ-16
15=a��t
a��t�͖��m���ł��D
�����a��t�����߂�ɂ͂ǂ̂悤�ɂ���Ηǂ��̂ł��傤���D
���ׂĂ݂�ƁC�A���������ʼn����K�v������̂ł��傤��
��낵����C�������������Ă��������܂����H
��̎��̉E�ӑ�ꍀ�����̎��̍��ӂŒu���������9=15-16�@�������a,t�͂Ȃ�
9=a��(t-16)
15=a��t
�̂��肩�ȁH
t = 225/14
a = (3 ��(14))/5
>>109
�㔼�͊ԈႢ�Ȃ̂œP��B
9=a��(t-16)
15=a��t
�̗��ӂ�����Z����2�悷���
(3/5)^2=(t-16)/t
9/25=(t-16)/t
(9/25)t=t-16
t=16/(1-9/25)=25
a=9/��(t-16)=9/��(25-16)=3 �O>>93�����B
>>92
9�l�ɖ��O������B
�A�J���A�C�T���A�E�~�A�G�C�^���E�A�I�T���A�J�i�G�A�L���^���E�A�N�~�A�P�C�R�B
�ƂȂ蓯�m3�l�g�ɂȂ�Ƃ܂�1�ʂ�B
�A�J���ƃC�T����2�l�Œ�ł���1�l�̑I�ѕ���7�ʂ�B
2�l�Œ�̓A�J���ƃE�~�ł��������A�C�T���ƃE�~�ł������B
�܂�3�~7=21(�ʂ�)
2�l�Œ��1�O���[�v�ł�����2�O���[�v�ł��悩�������A3�O���[�v�ł��悩�����B
21�~3=63(�ʂ�)
����1�l�Œ�����A�ʂ̃O���[�v����2�l����Ă���B
���Ƃ��A�J���Œ�ŃG�C�^���E�ƃI�T������Ă���B
�Œ肪3�ʂ�A��Ă���͓̂��O���[�v������Ȃ�6�ʂ�A
�ʃO���[�v����1�l���Ȃ�3�~3=9(�ʂ�)
3�~(3+6)=27(�ʂ�)
���킹��63+27=90
3�l�Œ�ł��Ƃ�2�O���[�v�̕�������(6C3)=6�~5�~4/(3�~2)=20(�ʂ�)
���Ԃ肪�C�ɂȂ邯�ǁA
90+20=110(�ʂ�)
�m���Ȃ͂���܂肠�Ăɂ��Ȃ��B >>113
�m���̖��
����׃`�[���������Ă��邵��
(1)�A�J���ƃC�T���������`�[���Ɋ��蓖�Ă���m���͂����炩�H
(2)�A�J���A�C�T���A�E�~�������`�[���Ɋ��蓖�Ă���m���͂����炩�H >>115
(1) 3*7!/(3!3!) / (9!/(3!3!3!))
(2) 3*6!/(3!3!) / (9!/(3!3!3!)) (1) 3*7!/(3!3!) / (9!/(3!3!3!)) = 1/4
(2) 3*6!/(3!3!) / (9!/(3!3!3!)) = 1/28
>>115
(3)�A�J���A�C�T���A�E�~�� 3�`�[���Ɋ��蓖�Ă���m���͂����炩 ���̕����ȒP
(1)
�A�����@�������@�������@2/8=1/4
(2)
�A�C���@�������@�������@1/7
(1)*1/7=1/28
(3)
�A�����@�C�����@������3/7
1-(1)=3/4
3/4*3/7=9/28
�����������ăV�~�����[�V����

> c(1/4,1/28,9/28)
[1] 0.25000000 0.03571429 0.32142857
�ɋߎ��������ʂ�����ꂽ�B �y�j���̓����i��{�A�Q�����j�łX�D�Q���~�Q�b�g�B
>>124
���C��Ɠ������i��wwww
�A�z�` >>125
�R�X�g�p�t�H�[�}���X�ǍD�ȐE���(�E�́E)��!! >>126
�Ȃ��A�}�N�h�̃o�C�g��wwww
���Ԓm�炸�̔\����wwwwwwww
�O��̈�t���Ǝ����č��N���猤�C�����Ă�m�荇���ɕ������炠�蓾�Ȃ����Ă�
�A�z�`wwwwwwwww �O>>116
>>86
���������J�f1�C�ƃI�����W���J�f1�C�̑��̐��𑫂��ƁA
240+160=400
6�C���Ȃ�400�~6=2400(�{)
2240�{�ɂ��邽�߂Ƀ��������J�f��4�C�A
�I�����W���J�f��8�C�ɂ���ƁA
240�~4=960
160�~8=1280
960+1280=2240(�{)
�����������J�f4�C�A�I�����W���J�f8�C �O>>128
>>88
A�N��B�N�AC�N�AD�N�AE�N�AF�N��5�l�̂����̂��ꂩ�Ƒg��Ń`�[�������ƁA
�c��4�l���ǂ��g�ނ��́A���Ƃ���A�N��B�N�Ƒg�Ƃ��āA
C�N��D�N�AE�N�AF�N��3�l�̂����̂��ꂩ�Ƒg�ނ��ƂŁA
���Ƃ���C�N��D�N�Ƒg�Ƃ��āA
�����I��E�N��F�N���g�ނ��ƂɂȂ�Ƃ����ӂ��Ɍ��܂邩��A
5�~3=15
��15�ʂ� >>127
���C��͒P�Ɛf�Â͋ւ����Ă��邩��
�O�Ńo�C�g�Ȃ�Ăł��낤�B �`�N�A�a�N�A�b�N�A�c�N�A�d�N�A�e�N�AG�N�AH�N�AI�N�AJ�N�̂P�O�l�����܂��B�R�l�A�R�l�A4�l����Ȃ�R�`�[���ɕ����܂��B
�`�[�������͉��ʂ�ɂȂ�ł��傤�H
�Ⴂ���͂���Ă��~�}�ԓ���o�C�g
������h�N�^�[�J�[�̃o�C�g�͈�ӂP�R���������B
���ς��Ĉ�ӂłR��̏o�������������A�H�ɏo���O�Ƃ������Ƃ��������Ȃ��B�`�b�k�r�̃v���g�R���ɏ]���Ă̐S�x�h���̏o�O���d���B
>>132
���O����Ɠ������H
���C�ĂȂ����O�͌��C��Ɠ�������ł����Ȃ� >>133
2100�ʂ�
���Z�ɁA����v���O����������Ď��s�B
�ꍇ�̐��𐔂�����A�������̕�����������B
[1,] ABC DEF GHIJ
[2,] ABC DEG FHIJ
[3,] ABC DEH FGIJ
[4,] ABC DEI FGHJ
[5,] ABC DEJ FGHI
[6,] ABC DFG EHIJ
[7,] ABC DFH EGIJ
[8,] ABC DFI EGHJ
[9,] ABC DFJ EGHI
[10,] ABC DGH EFIJ
[11,] ABC DGI EFHJ
[12,] ABC DGJ EFHI
[13,] ABC DHI EFGJ
[14,] ABC DHJ EFGI
[15,] ABC DIJ EFGH
....
[2086,] DGI FHJ ABCE
[2087,] DGJ FHI ABCE
[2088,] DHI FGJ ABCE
[2089,] DHJ FGI ABCE
[2090,] DIJ FGH ABCE
[2091,] EFG HIJ ABCD
[2092,] EFH GIJ ABCD
[2093,] EFI GHJ ABCD
[2094,] EFJ GHI ABCD
[2095,] EGH FIJ ABCD
[2096,] EGI FHJ ABCD
[2097,] EGJ FHI ABCD
[2098,] EHI FGJ ABCD
[2099,] EHJ FGI ABCD
[2100,] EIJ FGH ABCD
2100�ʂ�ł����Ă���݂����B
>>135
��t���A�܂�����Ďł���������̂ɁB
���̍��͗Տ����C�͓w�͋`���ŃX�g���[�g���ǂ��f�t�H�̎���B
������Ɏs���a�@�ɏA�E����̂͏����h�������ȁB
���A��1�N�߂ňݐ؏��������Ă��炦���B�M�v�X���Ƃ��鉤�؊J�̏���Ƃ��O�ȈȊO�̎d���ɂ��]���ł����B
�O�Ȃ̓��^�C�A�������ǁA�������▃���̃o�C�g�͑����Ă���B
��t�ߏ�Ńo�C�g�̑�������ꂩ��ǂ�ǂ����Ă������낤�Ȃ��B >>136
100�������Ĉ�t���A�܂��������Ƃ��Đ��Ԓm�炸�̓��{�Љ�̊���A�ނ��Ƃ͂Ȃ� 10�l�̎q��(A,B,C,....,J)���R�`�[���Ɋ��蓖�Ă�B
�e�`�[���͂P�l�ȏ�̎q�������蓖�Ă���B
���ʂ�̕����������邩�H
��.
(A) (J) (B,C,D,E,F,G,H,I)
(A,C) (H,I,J) (B,D,E,F,G)
>>140
���l���̃`�[���͋�ʂ��Ȃ�
�q���͋�ʂ��� >>137
����ς�A�܂�����ˁB
���d��������Ă�́H �O>>130���ŁB
>>133
A�N(����)
10�~7�~3=2100
��2100�ʂ� �O>>144�����B
>>133
3�l�O���[�v��2�B
��肪����B
��105 >>144
C[10,4]*C[6,3]/2=2100�ʂ� �v�f��10�̏W������A�v�f��5�̕����W����10�쐬����B
�����10�̕����W���̂ǂ�2�̋��ʕ����̗v�f����3�ȉ��ł���Ƃ����B
���̂悤��10�̕����W�����\�����邱�Ƃ͉\���H
����
[,1] [,2] [,3] [,4] [,5]
[1,] 1 4 8 9 10
[2,] 2 4 5 8 10
[3,] 3 4 5 6 7
[4,] 1 2 5 6 10
[5,] 2 4 6 7 8
[6,] 3 5 6 8 10
[7,] 2 3 4 6 9
[8,] 1 2 3 5 9
[9,] 1 3 4 6 10
[10,] 1 4 5 7 9
2�s�̑g�ݍ��킹�Ƌ��ʗv�f�̐��𐔂���i1�ڂ̍s�ԍ��A2�ڂ̍s�ԍ��A���ʗv�f�̐��j
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 1 3 1
[3,] 1 4 2
[4,] 1 5 2
[5,] 1 6 2
[6,] 1 7 2
[7,] 1 8 2
[8,] 1 9 3
[9,] 1 10 3
[10,] 2 3 2
[11,] 2 4 3
[12,] 2 5 3
[13,] 2 6 3
[14,] 2 7 2
[15,] 2 8 2
[16,] 2 9 2
[17,] 2 10 2
[18,] 3 4 2
[19,] 3 5 3
[20,] 3 6 3
[21,] 3 7 3
[22,] 3 8 2
[23,] 3 9 3
[24,] 3 10 3
[25,] 4 5 2
[26,] 4 6 3
[27,] 4 7 2
[28,] 4 8 3
[29,] 4 9 3
[30,] 4 10 2
[31,] 5 6 2
[32,] 5 7 3
[33,] 5 8 1
[34,] 5 9 2
[35,] 5 10 2
[36,] 6 7 2
[37,] 6 8 2
[38,] 6 9 3
[39,] 6 10 1
[40,] 7 8 3
[41,] 7 9 3
[42,] 7 10 2
[43,] 8 9 2
[44,] 8 10 3
[45,] 9 10 2
�ׂ�
�i�q�_����Ȃ鐳�O�p�`�����݂��Ȃ����Ƃ�����
�̏��w���ł��킩��ؖ��Ƃ����̂��Љ��Ă�
���X�ʔ���
���_��ʂ�2�����@y=tx��y=ux�@�̂Ȃ��p����/3�̂Ƃ��@(t-u)/(1+tu)=��3
t,u�͂Ƃ��ɗL�����ł��邱�Ƃ͂Ȃ�
������2�̊i�q�_����钼���̌X���͂Ƃ��ɗL����������
�i�q�_�����2�����łȂ��p����/3�ł�����̂͂Ȃ�
�܂�
�E�ʐρ����²
�E�ӂ̌X��
�g���̂�����
�Љ��Ă���@��
�u�i�q�_����Ȃ鐳�O�p�`������ΕK�����̓����ɂ��i�q�_����Ȃ鐳�O�p�`���Ƃ��v
�������Ƃ������
�L�[��
�uA,B���i�q�_�Ȃ�A���S��B��90���Ă��i�q�_�v
���g��
�܊p�Ȃ̂ŁA>>152�ɕ⑫
(0,0),(a,b),(c,d)���i�q�_����Ȃ鐳�O�p�`���Ƃ���ƁA
(a,b),(d,-c),(b+c,-a+d)�̎O�_���i�q�_����Ȃ鐳�O�p�`�ŁA����L��菬�����B
�����ɁA��菬���Ȋi�q�_����Ȃ鐳�O�p�`�������������Ƃ��\�ƂȂ薵���B �f���炵��
�ׂŏЉ��Ă��ؖ�
���Ȃ݂ɓ����v�̂�n��5�Ő�n�p�`�������Ȃ̂������܂�


EBD���ӎO�p�`�ł��邱�Ƃ��ǂ����Ă킩��̂ł����H E������������AED=75���ł���悤�ɂƂ��Ă���
����Ǝ����I�Ɂ�EBD�͓ӎO�p�`
�ʐς��ׂĂ݂�Ɖ��̐}���番����ʂ�
��EBD = 1/2 AD (1/2AD) = 1/4 AD²
��ABD = 1/4 AD² (�����`��1/4)
�Ł�EBD�́�ABD�̓��ϕό`�ł���(��ӂ�ς�����A��E��BD�ɕ��s�ȃX���C�h)�Ƃ킩��
>>156
���ꂾ�Ɗ̐S�̎O�p�`EBC���O�p�`�ɂȂ邩(EDC�������ɂȂ邩)������Ȃ��B
>>155
E����BD�ɉ��낵�������̑���H�Ƃ��āA�O�p�`EHD�����ɐ܂�Ԃ��AD�̈ړ����F�Ƃ���ƎO�p�`EFD�ƎO�p�`BDE�������ɂȂ�B�ؖ���F����ED�ɐ��������낵�Ē��p�O�p�`�̑������g���Ă����B >>157
�Ⴄ��
����CD�Ɣ�����BC��B���S��75�����̌����ɉ�]�������������̌�_��E�Ƃ����
�O�p�`�ɂȂ�Ȃ��킯���Ȃ� >>158
�����Ă邱�Ƃ̈Ӗ���������Ȃ����A>>156�Ƃ������Ă邱�Ƃ��Ⴄ�B
�Ă���������>>155�̓ڂ̉摜�Łu�C�Â��ɂ����v�Ə����Ă������>>156�͂�����������B
�܂��W���j�A�Z�I��������A>>157�قǂ����Ƃ��Ȃ��Ă��A75�x����C�Â�����Ă��Ƃ���B >>159
���O����҂���Ȃ�����H
�������炨�O�����l�̎���ɑ��铚���ɑ��āu���O�̌����Ă鎖�͕������v�Ƃ����̂����������؈Ⴂ���H
����҂��킩��Ȃ��Ȃ�Ƃ�����
�܂����̒��x�̍s�ԓǂ߂�l�Ԃ����l�ɐ��w�A�h�o�C�X�ł��郌�x���ɂ͂Ȃ��� >>160
���Ⴀ���߂Ă��ꂪ���₷���B
����CD�Ɣ�����BC��B���S��75�����̌����ɉ�]�������������̌�_��E�Ƃ����Ƃ��AE���uA��ʂ�BD�ƕ��s�Ȓ����v��ɂ���͉̂��̂ł����H >>161
�����炻�̐�����>>156���H
�����ׂ����Ƃ́�BAD�̖ʐςƁ�BED�̖ʐς������ł��鎖
��BAD�͒��p�ӎO�p�`
��ӂ̒����F������2:1�Ŗʐς�1/4BD² (����>>156�͊Ԉ���Ă�)
��BED�͂�͂�BD���ӂƂ݂��
��ӂ̍����F����= 2:1�Ŗʐς�1/4BD²
2�ڂ̂�͓������2���ڂ̉摜�ɒ�ӂƍ����̔䂪2:1�ɂȂ鎖���w�E����Ă�
���������uE���������ς��Ȃ��悤�ɂƂ������ӎO�p�`�ɂȂ�̂���������������v���Ɂu�t�ɓӎO�p�`�ɂȂ�悤�ɂƂ��č������ς��Ȃ����������Ȃ����H�v�ƍl����̂͏����̏퓅��i���H >>162
������A
>��BED�͂�͂�BD���ӂƂ݂�ƒ�ӂ̍����F����= 2:1��
�����E�����s����ɂ��邩��ł����āA�ӎO�p�`�ɂȂ�悤��E��������ꍇ�ɁAE�����s����ɂ��邱�Ƃ������Ȃ��Ƃ����Ȃ�����H������Ă���B >>138
�ꍇ�������Čv�Z������6010�ʂ�ɂȂ����B ����
[,1] [,2] [,3] [,4]
[1,] 1 1 8 45
[2,] 1 2 7 120
[3,] 1 3 6 280
[4,] 1 4 5 420
[5,] 2 2 6 630
[6,] 2 3 5 840
[7,] 2 4 4 1575
[8,] 3 3 4 2100
>>163
������
������Ƃ��O���x���Ⴗ����� >>166
�����Ⴄ�˂�w
�������Ȃ������瑊����Ȃ����āA�����p���������s�ׂ����ė������ė~�����ˁB
�܁A����̃��x�����Ⴉ�낤���A����̎���ɓ������Ȃ������͎̂����B���̃X���`���l�݂͂�Ȃǂ����������������������Ă��B ���̂����H
ABCD�̔z�u�킩���Ă邩�H
�R���͖�蕶�ɗ^�����Ă���H
�Œ���CD��Ɂ�EBC=75���ƂȂ�_�͎��܂��H
�Ƃ���ȁH
�����Ƃ�Ə�������ȁH
���̎���EBD�͓ӎO�p�`�ɂȂ���ď�������ȁH
�Ȃ�܂��H
��BED=30���A��BCE=30���Ȃ��EBC�͉��x�ɂȂ�H
�v�Z�ł��܂��H
���̎���EBD�͉��x�ɂȂ�H
�����Z�ł���́H
�����Z�ł���A�z���A�z�ƌ����ĉ���������H
�\����
�����A�ꃖ���~�X���Ă��
�ł����̃A�z�������\�����邩�珑���Ƃ���
��EBC=75���A��BCE=30���Ȃ��BECC�͌v�Z�ł��܂��H
180��-(75��+30��)���v�Z�ł��ˁH
����Ƃ��O�p�`�̓��p�̘a��180�����Ēm��܂��H
�A�z�ł����H
�ꍇ���������Ɍv�Z�ł���̂��낤���H
>>168
>>169
�͂��c(��)
���̂Ȃ��A���̖��̖ړI�������Ă�H
CB=CE�ƂȂ�ӎO�p�`�Ȃ�č�낤�Ǝv������Ɍ��܂��Ă邶���B
�l�p�`ABCD�̖ʐς����߂邽�߂ɂ͎O�p�`ABD�ƎO�p�`EBD�������ʐςł���Ǝ����Ȃ��Ƃ����Ȃ�����H���̂��߂ɂ͂����ӎO�p�`���܂����A����Ȃ��AE�����s����ɂ���Ǝ����Ȃ��Ƃ����Ȃ����낤���B
���A�W���j�A�Ƃ͂����Z�I���̖�肪����ȊȒP�Ȃ킯�Ȃ����낪w >>169
�����Ȃ�ɂ��������ĂȂ��̂�w
������������Ȃ��Ă����̂�����w >>171
�o�܂���
��ӂ��ǂ������Ƃ�
�m�邩
����҂́u�Ȃ��75���ɂȂ��ł����v�ƕ����Ă��o�[�J
���ۂ��̖��75���Ƃ���������ďؖ��ɂ�����̂͏����̎��H�e�N�j�b�N�ł�����H
�Ă���ӂ��ǂ����������Ă邯�ǂ��O�ق�Ƃ́�BED���ӎO�p�`�ɂȂ�ؖ��킩���������\����
���̃��x���œ˂��������Ă���Ȕ\���� >>173
�u���s�����E�������������Ȃ�75�x�ɂȂ��ł����H�v
�ɑ���
�u75�x�ɂȂ�悤�ɂ�������v
�������ɂȂ邩��w
��ӂ����Ă邩�炻��ȃg���`���J���ȓ������o�Ă����H
�Ă��{���ɖ��̖ړI�������ĂȂ�������B�m���ɉ摜�ɂ͏����ĂȂ����ǁA���ꂭ�炢�����邾��w
1:2�͂ǂ���������ww >>174
�_�[�J�[���[�Ȃ���Č����Ă���H
�A�z�ł����H
���Ⴀ���w���ł����H�ł���A���S���Y����75�����@�B�I�ɓ��o�ł����ł����H
�A�z�ł����H
�A���S���Y���͂���A����������Ȃ���O�p��K��������H
�������܂��ォ�`�H
�W���j�A���I���ł͂ǂ����܂����ĕ����Ă��o�[�J
���75�����Ȃǂ����ȁH�Ƃ�������ďؖ��ɂ�����͓̂�����O���H
�ŋt��75���ɂȂ�_�Ƃ��Ă��������̏��^�̓_�ɂȂ�̂������͕̂p�o�e�N�j�b�N���H
�܂����O�̃N�\���x���ł͂���ȃe�N�j�b�N�g�������Ȃ���낯�ǂȔ\�����N >>175
�u�Ȃ��������Ȃ��A�o�[�J�o�[�J�v
���x���ɂȂ��Ă�����w >>175
���A�Ō��
���w���ł�75�x�ƕ����邩����ɂȂ��Ă��B������O�����ǁB >>177
�܂����̃��x���̃A���|���^���ɃA���S���Y���Ƃ��A�[�I�Ɍv�Z�\�Ƃ������Ă��Ȃ�̘b���킩������
���̘b�����Ă���ăL�[���[�h�͎U��߂����X�������ǂ������Ӗ��킩�����
�v����ɂ��O�͎���������ɂ���Ȃ��ĂȂ������玩���ŔF���ł���J�X�Ȃ�
�o�[�J >>178
�������Ɍ��ꂵ���B��������ȁB �O>>144
>>155
AB=AD=5�o1/(1+��3)�p
�l�p�`ABCD=5^2/(1+��3)^2�p(1+��3/2)
=5^2(��3-1)^2(2+��3)/(2^2�E2)
=(25/4)(2+��3)^2
=(25/4)(7+4��3)
=(175+100��3)/4
��BED=72���Ƃ����肵�ĕʉ���
�o�����炨�����낢�����B ����̎�|�͎��B
��̎O�p�`������B��ӂ͓����B
����̎O�p�`�́A��ӂ̗��p�͋���45���B
��������̎O�p�`�́A30����75���B
���̎��A��̎O�p�`�̖ʐς͓������B
�K���ȕ⏕���������Ċm�F�\�B
(��ʂɂ́A�@sin(a)sin(b)/sin(a+b)�@=�@sin(x)sin(y)/sin(x+y)�@������)
��������m�Ƃ�����ŁA���̖����l����B
��̎O�p�`������A��ӂ������ŁA�ʐς��������B
����̎O�p�`�́A��ӂ̗��p������45���B
��������̎O�p�`�͒�ӂ̕Е���75���B
���̎��A�c��̓�̊p�����߂�B
�����́A30����75���B�m���ɉ�肭�ǂ��B
�O>>181�����B
>>155
AB=AD=5�o1/(1+��3)�p
�l�p�`ABCD=5^2/(1+��3)^2�p(1+��3/2)
=5^2(��3-1)^2(2+��3)/(2^2�E2)
=(25/4)(2-��3)(2+��3)
=25/4
=6.25
��6.25㎠ >>172
�u�������悤�v����u�����������Ă�낤�v�ɂȂ������Ō��������Ȃ�낤�ˁB
������Đ����ł��Ȃ����Ă��Ƃ̗��Ԃ��ŁA����������F�߂Ă�悤�Ȃ���ȁB���̐l�Ɍ��炸�B X=450,000+0.125Y+0.1Z
Y=720,000+0.1X
Z=367,500+0.1X+0.125Y
������X=600,000 Y=780,000 Z=525,000�ɂȂ�炵���̂ł�����@�������Ă�������
>>185
Y=720,000+0.1X
�𑼂�2���ɑ�������X��Z�̕��ʂ̘A���������ɂȂ�B X=450,000+0.125(720,000+0.1X)+0.1Z
Z=367,500+0.1X+0.125(720,000+0.1X)
X=540,000+0.0125X+0.1Z
Z=457,500+0.1125X
X=540,000+0.0125X+0.1(457,500+0.1125X)
X=585,750+0.02375X
0.97625X=585,750
X=600,000
�ł��܂����B���肪�Ƃ��������܂����I
5�b�œ�����
Q�@�s���͎���4Km�A��͎���6Km�ł���ƂƃR���r�j���������܂����B
���ĕ��ώ����͂�����ł��傤���H
>>188
���a���ςȂ̂Ŏ���4.8km >>188
���̎�����5�b�͖����ł���B�Q�Ă邩�N���Ă���Z�����B >>190
�������Ă�����Ă��Ƃł���B
�p�b�ƌ��āA4��6�̕��ς�5�Ƃ����Ⴄ�ƊԈႢ�ł���A�Ƃ������Ȃ��ǁA�L���Șb������ˁB >>191
���̃X���Ŏ���ɓ����Ă�l��ł���Ȃ��ƒm��Ȃ��l�͂��Ȃ����낤�ˁB
>>188�́u���O��A����m���Ă邩�H(��ԧ)�v���Ċ����������낤����w
�����Ȏ��₶��Ȃ��āA����m���Ă邩�n�̓z���g�낭�Ȃ̂Ȃ���w ����m���Ă邩�nw
�܂��A���������X�x����w
�����Ƃ����̒��P���w�̖�肪���\����
����͎���������悤�Ȏq�ɂ����킹�Ă�Ǝv����
����T�N�T�N�Ɖ�����H

�l���v�Z�̃��[����S���Ԃ�����ł邩�炫����i�������������j >>196
�����I����7/4�ɂȂ������Ǎ����Ă��� ���������njv�Z�����ƎႢ�Ƃ��ɂ͂��蓾�Ȃ��悤�Ȍv�Z�~�X�����肵�Ăğ����ɂȂ���
���x��C��t���Ă��ǂ����Ă��Ԉ���Ă��܂�����ǂ����悤���Ȃ�
�O>>183
>>185
X=450,000+0.125Y+0.1Z
Y=720,000+0.1X
Z=367,500+0.1X+0.125Y
Y-Z=352,500-0.125Y
X+Y-Z=802,500+0.1Z
X+Y=802,500+1.1Z
8X+Y+0.8Z=3,600,000+720,000+0.1X+0.08X+0.1Y
7.82X+0.9Y+0.8Z=4,320,000
-6.82X+0.1Y=-3,517,500+1.9Z
0.1X+0.1Y=80,250+0.11Z
6.92X+1.79Z=3,597,750
X+720,000+0.1X=802,500+1.1Z
1.1(X+Z)=82,500
X+Z=7,500
1.79X+1.79Z=179�~75=53700/4=13,425
5.13X=3,584,325
X=358,432,500/513
=119,477,500/171
Y=720,000+11,947,750/171
=123,120,000/171
Z=7,500-X
=7,500-119,477,500/171
=(1,282,500-119,477,500)/171
=-118,195,000/171 �O>>199
>>185
80X=36,000,000+10Y+8Z
10Y=7,200,000+X
80Z=29,400,000+8X+10Y
��2���ӁX������79X=43,200,000+8Z
��2���ӁX������80Z=36,600,000+9X
�ӁX������70X+72Z=79,800,000
�ӁX������79X-80Z=6,600,000+8Z-9X
88X-88Z=6,600,000
X-Z=75,000
35X+36Z=39,900,000
35X-35Z=2,250,000+375,000=2,625,000
71Z=37,275,000
Z=525,000
X=75,000+525,000=600,000
10Y=7,200,000+600,000=7,800,000
Y=780,000 ��1�p�h������1���������̕��͑�ł��B
���������߂邽�߂̎�����邱�Ƃ͂ł����̂ł��������܂���ł����B
���͉��L�ŁA�����Ă������܂ł͍����Ă��܂����B
(175+x)/18=(920-x)/55
�ł����v�Z�̍ہA�ʕ����悤�Ǝv�����̂ł����A18��55�̌��{�����v�������l��ł��܂��܂����B
�v�Z�@�T�C�g���g�p�����Ƃ���A���̗����̍ŏ����{����990�������ł��B
���ۂɉ����Ƃ��A��990�܂Ōv�Z���邵���Ȃ��̂ł��傤���H
����Ƃ������ƃX�}�[�g�ȉ�����������̂ł��傤���B
�h�����̉y�[�W�ɂ́A���͂���̎��̏o�����Ɠ���(x=95)�͍ڂ��Ă��܂������A�������߂�ۂ̌v�Z�͏Ȃ���Ă��܂����B
990���|�����Ȃ���18*55���|�������
������̂��ړI�Ȃ̂�����990�Ƃ����ς��v�Z���邱�ƂɈӖ��͂Ȃ�
>>202
�P�W���Q✕�R✕�R
�T�T���T✕�P�P
���킩��Ό��{���͏o����Ǝv�����B �ꎟ�������̉����������Ɏ��ɕ����������
�ŏ����{����S���Ɋ|���ĕ���������������������ԈႤ
�ŏ����{���������肶��Ȃ����낤��
�f����18*55�|���Ƃ����Ęb
>>203
��������߂�18*55���|����Ηǂ��ƌ����̂͂킩��܂���
(990��18��55�̐ςł������ł���)
>>204
���P�W���Q✕�R✕�R
���T�T���T✕�P�P
�����킩��Ό��{���͏o����Ǝv�����B
�������͂悭����܂���
�A���@�H�ōŏ����{�����������Ƃ�����
5*5*7*2*2*2*23=32,200�ɂȂ��Ă��܂��܂���
>>206
���݂܂���A�����ʕ������蕪����Ƃ��ɍŏ����{�����g���Ă����̂Łc >>207
>>204������Ε�����悤�Ɍ����Ȃ�����2*2*3*5*11���ŏ����{���ɂȂ�͂�����
�Ă�7�Ƃ�23���ǂ�����łĂ����̂��m�肽���B 18��f�������������Ƃ��̎w������ׂ����(1,2,0,0,0)
55��f�������������Ƃ��̎w������ׂ����(1,2,0,0,0)
2�̗�̑Ή�����e��������ׂđ傫������I��ŕ��ׂ��(1,2,1,0,1)
2^1*3^2*5^1*7^0*11^1=18*55=990�ł��ꂪ�ŏ����{��
2�̗�̑Ή�����e��������ׂď���������I��ŕ��ׂ��(0,0,0,0,0)
2^0*3^0*5^0*7^0*11^0=1�ł��ꂪ�ő����
������
������Ƃ��ɍŏ����{���g���̂͌�̎�Ԃ��y�ɂ��邽�߂ł����Ȃ�
���̂��߂Ɏ��Ԃ�ׂ��ċl�ނ̂ł͖{���]�|��
�S�`���S�`���l�����ɕ�����ق������{�}�V
�������͂킩���Ă�̂ɂ��������I�Ȍv�Z�~�X���肵�Ă邩�礂��傤���Ȃ�

�i�j�ł������������|���Ȃ��ňڍs�����Ⴄ�����Ȃ������Ȃ� >>209
�����͑f���ׂ̂��w���̗L���g�ŕ\���邩��
�������g�����đf���ׂ̂��w���̖����g��
�g��������\���Ȃ�����
�a���ǂ���`����邩
�F���ۗ��_�łȂ�Ƃ��Ȃ��łȂ��H >>202
�ʉߎZ�̗ނ��ȁB
���̑����ő����Ԃ�����175m�̓S����n��n�߂Ă���n��I���܂ł�18�b�|�������B�܂��A������Ԃ�����920m�̃g���l����ʉ߂���ۂɊ��S�ɉB��Ă������Ԃ�55�b�������B��Ԃ̒��������߂Ȃ����B
�̂悤�Ȗ���z���B
�f���ɗ�Ԃ̒�����xm�Ƃ��đ�����x��p�������ŕ\���Ă��ǂ����ǁA��Ԃ̑�����b��xm�Ƃ��Ē�����x��p�������ŕ\���Ă��ǂ��B
18x - 175 = 920 - 55x
�����x�����߂Ă��炻���18x - 175�ɑ�����ė�Ԃ̒��������߂�Όv�Z�͑����邯��18��55�̌��{���͋��߂Ȃ��čςނ�B
���������S�������Ⴂ�̖�肾�����炲�߂�ˁB �O>>200
>>202
(175+x)/18=(920-x)/55
175�~5�~11+73x=9200+7360
73x=16560-8750-875=7810-875=6935
x=95
��6935-6570=365=73�~5 ��̖�肾���Ǥ����ō����Ă�H

���̖���
�uA����̏�������B����̂Q�{�ł���A2�l��200�~�̖{������A����̏�������B�����3�{�ɂȂ����v
B����̏�������X�~�Ƃ��ĕ����������ꍇ
X-200��3�~2X
�ɂ��Ă����Ƃ��Ă͐����Ȃ́H
2X-200��3�iX-200�j���������������ǂ�
�m���
���Ȃ�
A��2B
A-200��3�iB-200�j
�Ƃ����������Ă��
>>221
�s��������
���ꂾ�ƁwB����200�~�̖{������B����̏�������A�����3�{�ɂȂ����x���� >>223
�Ȃ�قǁA�����搶�Ȃ灛�����ꂻ�������Ǐ��q�ɂ����D���������R���搶�Ȃ炨�������~��t���������� >>224
�N�͔���������Ȃ��̂��� >>224
������X�̒l�������Ă��������ˁB�m��ǁB
����͍����ĂȂ�����~�m���ˁB ���������-200���ڍs�����200�ɂȂ邩�c���႟�~����
������Ƃ��̖��̎����Ӗ��킩��Ȃ�
A�s����B�s�ɍs���̂Ɏ���12km�̎��]�Ԃōs����莞��30km�̎����Ԃł�����2���ԑ�������
A�s��B�s�̓��̂��Xkm�Ƃ���A�s��B�s�̓��̂�����߂Ȃ���
�ƌ������Ŏ���
X/12-X/30��2�ɂȂ蓚�́@40km�Ȃ���
�ǂ��������R�ł��̎��ɂȂ�̂��悭�킩��Ȃ���N�������ăv���[�Y
A�s����B�s�Ƀ`�����ōs�������Ɋ|���鎞�Ԃ�X/12�i���ԁj��
���l�ɎԂōs�����Ɋ|���鎞�Ԃ�X/30�i���ԁj�Ȃ̂͂킩���
>>228
���]�Ԃōs����莩���Ԃōs������2���ԑ����������Č����Ă邩��B
X/12��X/30�����ꂼ�ꉽ��\���Ă��邩�͕������Ă���킯������A���Ƃ͂��̍���2���Ԃ��ĕ����𐔎��ɕ\�������B ���A�������x�����������Ԃ��瑁�����������Ԃ��������̂�2�Ȃ�
���肪�Ƃ���
�O>>220
>>221
B����̏�������x�~�Ƃ����ƁA
A����̏������͂Q�{�ł��邩��2x�~�B
2�l��200�~�̖{������A����̏��������A
2x-200(�~)�ŁA
B����̏�����x-200(�~)��3�{�ɂȂ�������A
3(x-200)=2x-200
3x-600=2x-200
x=600-200
=400
��400�~ �O>>228
>>231
2���ԑ����������Ă��Ƃ́A
�s���̂ɂ����鎞�Ԃ�2���ԒZ�����Ă��Ƃ�����A
X/12-2=X/30
X/12=X/30+2
5X=2X+2
3X=2
X=2/3
��A�s��B�s�̓��̂��2/3km
���悻667m�ɑ�������B �O>>232�߂�����B�����B
>>231
2���ԑ����������Ă��Ƃ́A
�s���̂ɂ����鎞�Ԃ�2���ԒZ�����Ă��Ƃ�����A
X/12-2=X/30
X/12=X/30+2
�ӁX60�{����ƁA
5X=2X+120
3X=120
X=40
��A�s��B�s�̓��̂��40km ���̖�荇���Ă�H

48x1.414=67.872.
32x1.732=55.424.
�v�Z�Ԉ���Ă��Ȥ����𐳐��ɂ���12�Ɩ�����X�b�L�������ɂȂ���
���̐��E���̐��̉��@���@�Ӗ��킩���B�d�g�݂Ƃ��������������ė~����
�i-5�j+3��-2
����5�~�����������v��3�~�o���̂ŕ���2�~�ɂȂ���
�i-5�j+�i-3�j��-8
����5�~�ɍX�ɕ���3�~�lj����ꂽ
�i-3�j+5��2
5�~���������o���3�~�o������2�~�����c��Ȃ�����
�i-5�j-�i-3�j��-2
���ꂪ�킩��ɂ����������ǁi-5�j���o���_�@�^��-���w����������i-3�j��-���u�w���ɏ]�킸���ɓ����v�Ɖ��߂��ė�������
�i-5�j�̈ʒu����-3����������ƌ����w���Ɂi-�j���������ċt��3�オ��������ē�����-2�ɂȂ�킯��
���������������Ă݂�


>>242
����A�܂Ƃ��ɗ������l����ƃz���g�ɖʓ|�Ȃ�B
���ʂ͌`���I�����ōς܂����c�B ���̒��P�̋��ȏ��ɍڂ��Ă�u���̐����܂߂��v�Z������@���v����
���a�̍��̋��ȏ��ɂ͍ڂ��ĂȂ������C������
�v�Z�̈Ӗ��ɂ͋����Ȃ��̂Ō`���ɂ��Ă܂Ƃ߂�B
�E�����̐��̋K��(1)
3=+3�A-3�A0=+0=-0
������+��t���Ă��ǂ�
������-��t���Ȃ���Ȃ�Ȃ�
0��+��t���Ă�-��t���Ă��悢
3=0+3�A-3=0-3�A0=0+0=0-0
�E���@�ƌ��@�̋K��(2)
+(+3)=+3�A-(-3)=+3
-(+3)=-3�A+(-3)=-3
�E�v����ɉ��@�ƌ��@�A�����̐��͋K��(1)(2)�ɂ��S�Ē�܂�B
++3=+3=3�A--3=+3=3�A
-+3=-3�A+-3=-3
�E��@�Ə��@�̋K��
(+5)�~(+3)=+15=15�A
(-5)�~(-3)=+15=15�A
(+5)�~(-3)=-15�A
(-5)�~(+3)=-15�A
�����̋K��͉��@���@�Ǝ��Ă��邪�A��@�́~�̑O�ɂ��鐔���̕������W���鏊���Ⴄ�B
���@�̕����͏�@�Ɠ����B
������5��3=5/3�ƋK��B
�����̐��̌v�Z
������
+5+3=+(5+3)=+8=8
-5-3=-(5+3)=-8
�ٕ���
+5-3=+(5-3)=+2=2
-5+3=-(5-3)=-2
�����A�揜�Ƃ��ɓ������A�ٕ����ŏꍇ���ċ@�B�I�Ƀ��[����K�p���邱�ƁB�Ӗ��t���h�͌��ǃx�N�g��(�ړ��̌����Ƒ傫��)�Ƃ��Ĉ������ƂɂȂ�Ǝv���B
�܂�����Ȃ��^������l�͔n���Ȃ낤��
�l�^��������n��
�E�����̊���Z�̈Ӗ��Ƃ�
�E�}�C�i�X�~�}�C�i�X���v���X�ɂȂ闝�R�Ƃ�
�Ɏ������߂Ή��Ƃ��Ȃ�Ǝv���Ă�n��
�E�݂���̑����͈�l���̌��~�l�����l���~��l���̌������
�E�͂����̐�����
�E~�̖�蕶�̓��{�ꂨ�������Ȃ��ł���
�Ƃ��n���������^�������
�u���钆�w�Z�̑S�Z���k1000�l�̂���45�������q���k�ł��餒j�q���k�������l���]�Z�����̂�
�S�Z���k��50�������q���k�ɂȂ�����]�Z�����j�q���k�̐l�������߂Ȃ����v
���@100�l
��̊w�Z����100�l�]�Z������Ă��蓾�Ȃ��ł���w�ǂ���Ȃ�
���͑�́u�ݒ�L�蓾�Ȃ����v�̎w�E���B
�H�����̔Z�x�ŗL�蓾�Ȃ��ݒ�̖�肪�ǂ����ŏo�肳�ꂽ���Ƃ�����炵���ȁB
�u��40�A��37�A�{�l12�A��(�܂��͖�)10�Ζ��v������(����͕����̖��_���܂�)�B
�ǂ��������Ȃ��b���B
�V�������w�Z���ł����Ƃ��Q�O�O�O�l�ア�������P�^�R���炢�V�����ق��Ɉڂ������Ƃ�����B
���ʂ�̓��ɑS�Z�W��Łu�����̓��͂��悤�Ȃ�v���̂��Ă���
>>256
�u����ȔZ�x�̐H�����͑��݂��Ȃ��v�������Ȃ�Ȃ��H
�������w�E�ł��邩�ǂ�����₤�Ă���̂ł� �Ȋw����肾��������Z�x�̌v�Z�͂ق�Ƃɋ�ɂ�����l�̎����ł��B���킵����
�����������Ɋ֘A���Ċb��
�u���������݂��悤�����܂����A���z�͂���v
�u�ł���E�ł��Ȃ����l���Ă�z�͌��ǂł��Ȃ��A���z�͂���v
�ۂŖ��i�g���̕������B�܂�����Ƃ���Ƃ̗���Ŕ��������瓖�Y��Ƃ̌o�c���Ԍ��S�����^����b�
�����A���ꂪ���ݐi�s�`�ŏ��a���瑱��������Ƃ̍����_�
�R���i�Ђɓ���O��2018�N�̎��_��68.2%���̓��{������Ƃ��Ԏ��Ȃ̂�������
�����̊F�͒m��Ȃ����낤���ǁA���ɒ�����Ƃ͉�œI���q������痈���œI�l��s����
�O���l���ق�Ȃ���Βׂ���Ƃ��������B�w�O���l�Ȃ���邩�璆����Ƃ̎��������x�Ȃ�Č����Ă�z��
������m��K�L���_�̂܂ܑ�l�ɐ������w���{���ゲ���I�x���Ђ��̖����S�n�Ȓ����N����
M&A������Ȃ�����A�ł͂Ȃ��B�w����]�ƈ��ł͂Ȃ��Ԑڏ]�ƈ��̐l�����팸���Ȃ��x�w���F�B�o�c�x��
�w�d��B�́g�d�v�Ȏ������ׂ̈̉�h�Ə̂����g������h��g�S���t�ۑҁh�Ȃ�etc�x����Ђ�H���ׂ��
������B���ׂ̃R�X�g�팸�Łw��Ђ̖��������ڐ�̎�Z�Ȑ��ʁx�����߂����ʂ����̏
�X�Ɍ����A���b��́w�S���I���S���x�Ɋւ��āA���{�`���̋��߂���c����Љ�ɂ��Ђ��̐��ɂ��
�w�S���I���S���x���Ȍ���͕s�s����ł����s����ꗬ���A�����
�l������ݔ���������w�s�����������A�����ƍi��邾��x�ƍi���ė������ʂ��A����
�����̍s���~�܂�w�����~�܂�x�̐��オ�K��関��������ė��邩���m��Ȃ�
>>253
���N����A��w�����ꎟ�����̓��e����ϊv����āA������ǂ�ł����lj�����
�����̃f�[�^���玿��ɍ������������悤�Ȗ�����ƂȂ����B
������A���͂̈Ӗ��Ƃ����������̂��ɂ���Ƃ����͎̂���̗��ꂾ���A���ەW��������~�߂悤���������ƁB >>263
���͌����̂悤�ȎU�z�}��ǂޖ����������ȁB �����Ă��������B

�l�p�`�`�a�b�c�Ƃd�e�f�g�͍������Ƃ��܂��B
���̂ӂ��̎l�p�`���A90�x�ł͂Ȃ��p�x�ŏd�Ȃ��Ă��܂��B
�l�p�`�g�h�i�j�͕��s�l�ӌ`���Ƃ������Ƃ͂킩��܂����A
���ꂾ���łȂ�4�ӂ̒������������Ђ��`�ł��邱�Ƃ��e�q�Ƃ��ǂ��[���ł��܂���B
���w�Z���x���̘b�ŏؖ����Ă��������B I����CD��EF�ɐ����������ďo����O�p�`������������HI��JI
�����ƊȒP�ɏؖ��ł������B�m��ǁB
>>265
�Ȃ����s�l�ӌ`���ƕ��������̂ł����H �Ă�HJ�����ԂƂg�h�i�j�͕K���g�h�̐��Ώ̂ɂȂ�ˁB
>>267
�ۈ����䍂��āA���܂���Ƃ��Ȃ��̋�Ӗ��������ł��܂����B
���肪�Ƃ��������܂����I�I �E�ƌP���w�Z�̎�����肪���P���w���x���Ȃ�Ȥ�������ɂ���������Ȃ��ƒm���ስ��������
>>271
�z���g�͎O�p�`�̍������������邩��A�ǂ����Ă����w�Z���x���ɂȂ�Ǝv���B �l�p�`BCKH�𗠕Ԃ���KC��KF�ɏd�Ȃ�悤�ɂ���iK�̓s�b�^���d�˂�j
���̂Ƃ��AABCD��EFGH�������Ȓ����`�ł���Ȃ�ABH��GH�Əd�Ȃ�
�܂��A��CKH�Ɓ�FKJ�͋��ʂœ������̂�����H��CD��ɂ���
�Ȃ̂�H��J�Əd�Ȃ邱�ƂɂȂ�
�]����KH=KJ
>>275
�����`�Ƃ͌����ĂȂ���Ȃ� ����҂������������ƌ����Ă��Ȃ��������Ǝv��������
���Ȃ��Ƃ�AB∥DC����Ȃ��ƕ��s�l�ӌ`�ɂȂ��
>>137
�Z�~���^�C�A���Ă�����100���~���炢�͂��邼�B
�̂̐E�ꂩ�疃���𗊂܂�Ă���̂��傫�����B
����m�ۂ����܂ł̃s���`�q�b�^�[�Ǝv���Ă����̂Ɋ���10 �������o�߁B�O���݂����ɑ��l�����肾�ƃR���i�����炤���X�N�����邯�Ǘ\�薃�����Ƃo�b�q�A���Ǘ�Ȃ̂ň������B
�~���ސE���Ă���Ɣ��������d��������Ă���B
��ŁA���̎d���͉��H ��1�h�����A���ʐ}�`�̍��ł�
�摜�̖�肪�����܂���
�ɂ́A(1)�̓�����40�x�Ƃ���܂��������������܂���ł���
�ʂ̔䗦�����Ŋp�x�����߂�ɂ͂ǂ�����悢�̂ł��傤��

���ȉ������������݂ɗ����Ƃ���Ń��X���������Ă��܂��܂���
>>286
���肪�Ƃ��������܂�
��CA���AB��ʂ��AC���Ǝv������ł����̂������ł���
A~B~C�̋t����������ł��� ���̎����đS�̂�0.05�|���Ă��r����100�|����5X�ɂ��邩��
���ǂ͌��̎����番��������̂Ɠ����ɂȂ��

���������Ďb���[�������Ȃ��������ǂ���Ɨ����ł��� ���������̂͂����Ȃ荶����v�Z���Ȃ���
�ʕ����Ă��������ق��������ˁB
500�~8/100��5/100�~800
���������
���ӂ�5/100�������邩��
�ÎZ�ł��ł���B
>>288
���ꎩ������u�ǂ̌�����������ł����A�Ȃɂ��\�L��̂��܂�Ȃǂ����ł��傤���H >>292
���܂�͖�������
��AB�����Č�ACB�Ɖ��߂��o������
����nj�CA����CBA�Ɖ��߂�������ɂȂ�� �O>>270
>>285
(1)��AOB=360��/(1+3+5)=40��
(2)��6^2/3=12��
(3)(4/9)2�E6=16��/3 >>294
�i3�j�͌�AC����Ȃ��Č�CA������
4/9����Ȃ���5/9����� �O>>294
>>293
�ς̌������v���B�����_�Ђ�⛩🐕
�ǂȂ́H�@�~�ʂ̌ʂ���Ȃ��́H ���Z�͂��ׂĊ��ƌ������Ƃ��ł���̂ł��傤���H
>>297
������
�l����ӂɌ��܂�Ȃ���Ί��ł͂���܂��� �������̓��͂���ЂƂ̏o�͂�Ԃ��������Z�ƌ�����Ȃ�����
�A��f(x,y)=0��x�ɑ���y������
����2�̉��i�o�́j�������Z�Ƃ��A�����̉������������Ƃ�������܂������B
>>301
�����̉������������@0x=0 �����͐����P���Ȃ̂ɍl������������ăh�c�{�ɂ͂܂�
���邠��
�O>>296�����B
>>285
(1)��AOB=360��/(1+3+5)=40��
(2)��6^2/3=12��
(3)(5/9)2�E6=20��/3 �������蒆�w���w�����蒼���Ă邪���ɐ��w��Q������̂��͂�����킩����
�O���O�ɉ��������͖����ēx����Ă݂���S�R�����Ȃ����Ĥ�܂��ŏ�Q������Ƃ����v�����
>>309
���₢��B�O�����o�����畁�ʂ̐l�͖Y���Ɍ��܂��Ă�B
���A���^�C���ŏK���Ă钆�w�������ĕ��K���邾��B����I���ۂ��͂Ƃ������B
�ŏ��̂����͂��̓��̂����ɕ��K���Ȃ��ƁB ��1�h�����A���ʐ}�`�̍��ł�
�摜�̖���(2)������܂���
�ɂ�(180���|30��)��2=75���Ƃ���܂�
180-30�܂ł͉���̂ł�������2�Ŋ����ł��傤���H
��OBA�Ɓ�OAB�̊p�x�����������Ƃ͂ǂ���������ł����H
���݂܂���A�摜��Y�t���Y��܂���

>>313
OA,OB�͉~�̔��a������A�������� O���~�̒��S�Ȃ�OA��OB�͔��a�����瓙�����A��OAB�͓ӎO�p�`
���������璼��150/2��75�ƌv�Z����ȁB
���������藝��������ˁB
���w3�N�ł��B
�����w�̌����҂��A�F���ɂ����͂̂���20���̋�͂ɂ��Ď��]�������ϑ��������ʁA
���S�ɋϓ��i50��50�j�ł͂Ȃ��A���̊�����51��49�Ƃ������ʂ����������ł��B
2%�̍��ƕ����ƈꌩ�덷�̂悤�Ɏv���邩������܂��A20���ϑ�����2%�̕肪�o��
�m����0.0000001%�ȉ��炵���̂ł��B
�܂�A���̕s�ϓ��͋��R�ł͂Ȃ��A�Ȃ�炩�̗͂���p���ĕs�ϓ��ɂȂ��Ă���Ƃ������̂ł����B
�O�u���������Ȃ�܂������A����i20���ϑ�����2%�̕肪�o��m����0.0000001%�ȉ��j
�Ƃ����̂͂ǂ̂悤�Ȏ����g���Όv�Z�ł���̂ł��傤���H
�O>>307
>>317
��=�o|���]�����E���-���]���������|/(���]�����E���+���]���������)�p�~100(%) >>317
�o�J����H���]��������
���ɑ��ĕ������߂�̂�
��Ԃʼn�]�͋[�x�N�g���\��
���̋[�x�N�g�����ǂ�2�ɐU�蕪����� �_�����e�͏ڂ����͊o���Ă܂��A���]�����Ƃ����̂͒n����̊ϑ������猩��
�E�E���̂ǂ������ʼn�]���Ă��邩�Ƃ����Ӗ��������Ǝv���܂��B
>>321
����ɒn�����猩�Ă���
�t���猩����t��]������
2���������
���̒�`�Ȃ�肪0���Ɍ�����_��
�K�����݂��邪�H �m��p�A���s��N�̃x���k�[�C���s�Ő����̉�X�Ƃ����X�̕��z��N>>0�ŕ���pN�A���UNp(1-p)�̐��K���z�ŋߎ��ł���
�����rN��ȏ�N����m����
P((X-pN)/��(Np(1-p)) > rN/��(Np(1-p)) )
= 1-2erf( rN/��(Np(1-p)))
erf�̒�`��wiki�ɍڂ��Ă邯�Ǐ������ŏ�����킯���Ȃ��̂Ō��Ǒ�搶�ɂ��肢���邵���Ȃ�
>>323
���̎q�Ɍ����Ă����傤���Ȃ����낤 >>319
����́u��v�̋��ߕ��ł����āA>>317�������Ă���A�u�肪�o��m���v�̋��ߕ��ł͂Ȃ� ���E�̒�`�͂ǂ��ł��悭�ĕ肪���邱�Ƃ��厖�Ȃ�Ȃ��́H
�O>>319
>>317
��=(|���]�����E���-���]���������|/200000)�~100=2
|���]�����E���-���]���������|=4000
��20���̂������]���̈Ⴂ��4�������A
���Y�肪�o��B >>314
>>315
�{�����c�ӎO�p�`�ł���
���肪�Ƃ��������܂��� >>317�Ŏ���������҂ł��B
��͂̎��]�����̘b�́A���̂��̎�����������Ƃ����o�܂�������邽�߂ɁA�ǂ����̑�w��
�����҂��q�ׂĂ������Ƃ����p���������ł���A���ꎩ�g�ɂ��Ď��͂悭�m��܂���
�F���̎��ɂ��ċc�_�������͂���܂���ł����B
�m�肽�������̂́A�Ⴆ�Ίm����x�A�ΏۂƂȂ����a�A���b�Ƃ������Aa��b��
���ꂼ��l��^�����x�����܂鎮�ł��B
1����3%�̕肪�o��m���́H�A100����1%�̕肪�o��m���́H�@�Ƃ������ł��A
��������Ό��ia�j���ib�j���ς���Ă��m���ix�j�������ɏo�邩�Ǝv���܂��B
�F����̘b�𑍍�����ƁA�����o�����͂ł��Ă��A���w�ŏK�����w�͈̔͂ł͂Ȃ�
�Ƃ������Ȃ̂ł��ˁB
�F�X�����肪�Ƃ��������܂����B ��������1/4�Ŗ{����c��̋��z��2/5���o���ĐH�ו�������540�~�c����
�͂��߂Ɏ����Ă����������͂����炩�������
�O>>329
>>332
3/4��3/5��540�~������A
���̋���540�~��(4/3)(5/3)
540�~20/9=1200
��1200�~ ������������Ă�̂ɓ���������������l�̋C�������킩��Ȃ�
>>336
���͂��O�ƈ���ĕ�����B >>339
��芸�����l�̋C������������Ȃ��͍̂Œ�Ȃ̂ŕ�����悤�ɂȂ��B >>341
���������Ă���l�ԁ�������
���������Ă��Ȃ��l�ԁ�������Ȃ�
��ʂł��Ȃ��̂��B
���O���n���Ȃ͕̂�����B ����������A�v�������肨���ʂ�����
��܂����Ƃ��������������ĉ�������ł���H�ŏ�����킩���Ă�����
���t�����Ǝv���ĉ��ɏ����Ă��̂�w
�������Ƃ��S���Ȃ�
�l�̋C������������Ȃ��Ƃ����Ƃ����ᔻ���Ă���
�l�̋C������������Ȃ��Ƃ������ƂC�ŏ������݁A�n�����N���̂͂�߂悤
>>343
���ǁA�ォ�珑�����ސl�Ԃ̋C���������������̂��H >>339
���͑�Ɍ������b�ł͂Ȃ����̕���ł���o���͗L�蓾��B
��o�����i�D�����Ƃ������Ƃ͖����̂ŁA�ォ�珑�����ސl�Ԃ̋C�������������Ă���Ƃ������Ƃ̏ؖ��ɂ͂Ȃ�Ȃ��B�ނ���S���������Ă��Ȃ��B �l�̋C�������킩��l�ԂɂȂ�ƌ����Ă�
�l���o�J�Ă�肷����Ăǂ������C�����Ȃ낤
�o�J�����狳���Ă��������i�j
>>348
�����Ȃ��B
���w���E���w�����x���̐��@�͂������������O�ɂ́u��(���l)���狳��鎑�i�v�������B�e���狳���ƌ��������Ƃ��낾���A�����������O�̐e�̋��炪�������Ȃ̂ł���������Ƃ���łǂ��ɂ��Ȃ�Ȃ������ȁB���O�͔n���e�̋]���҂Ȃ̂����m��Ȃ��B�e�q�����Ĕn���B ���̒��x�̎��Ő�܂����Ƃ������Ě}����l�Ԃ����邩��
���Đl����u���{�l�ɂ͎��₵�Ă��}�����畎�̂������ŋ����Ă���Ȃ��l�����\�����v�Ƃ���������Y
����ɑ���́A�����������Ɠ����ĂȂ����45����A���ȔF���m�F���K�v�Ȃ��炢�̐l�ł��鎖����ڗđR
�l�̓������}�E���e�B���O�����s�ׂ��Ă�킯����Ȃ�����������
���ꂱ�����Ō��������Ă錩�������Ă�A�Ă��Ƃ��ĕ�����˂���
�g��������������A�s�[������
�t�ɗi�삵�Ă�z���ʂɖ�N�ɐ����ĕ�����Ƃ��������͗ǂ�������
���̂܂�o���Ŕ��_�Ȃ�ĕ������^������ȋ���Y
���ŋ���Y��3�l�������H����Y�Ȃ�ĉ�1�l�����邾���ł�����I�[�o�[����
>>340
�搶�Ƃ肠����>>335���ǂ������C�����Ȃ̂������Ă��������B ���{�l�ɋ�M����ā����l���Εa���Ă�w
>>351
���͋����Ȃ��B�e���狳���B �n�� : ~����l�̋C������������Ȃ�
�� : ~����l�̋C������������B������Ȃ��n���͒p���������B����𑼐l���狳��낤�Ƃ���ȁB�e���狳���B�ǂ����e�������悤��(�l�̋C������������Ȃ�)�n�����낤���ǂȁB
�_�_1 : �l�̋C������������Ȃ�=�n��
�_�_2 : �l�̋C�����𑼐l�ɕ������Ƃ���=�n��
�_�_3 : �n���ƒ�ɂ�����n���̘A��
���̃o�J��ɓV��ɂȂ��Ă鎩�̌����l�i��j
>>354
���Ȃ��͎��̋C�������킩��Ȃ��̂ł����H
���Ȃ���n���ɂ��Ă���̂ł��悗 >>356
������ǂݕԂ��Ă݂���
�n�����̐��𗧂Ē������Ƃ��Ă������x���B�n���͏c�����x����� >>335
�������ɂ��Ƃ����˂���Ĕ���������� >>358
���������א����n���̏؋�
���͂����ł͂Ȃ� >>341,343,352, 358
�E�ɂ��Ƃ����˂��ꂽ
�E����������
�����̐��ʏ�
�m���ɐl�̋C������������Ȃ��n��(�ǂ�)��������
���Ȃ݂ɉ��͌�o������l�Ԃ̋C������������Ƃ͌����Ă��邪��o�����邱�Ƃ̐������͂��Ă��Ȃ� ���O�͉��̋C�������S���������ĂȂ�
���̔n���́u������i�삷��̂͂��������A�{�l���낤�v�Ɛ��ʂ������B�����łȂ��ԈႢ���B
���͌�o���̗i������Ă��Ȃ����u�l�̋C������������Ȃ��n���v��@���Ă���̂����A���̔n���͎������n�����ƌ���ꂽ���Ƃɑ��Ĉӎ��I�����ӎ��������邾����
���̔n���̐��̂̌�����P���Ȋ���͂悭������B�S���������Ă��Ȃ��Ƃ������Ƃ͑S�������B
�������ܔ������ł���b�����҂���������
�܂��O��I�ɒ@���Ēɂ݂�A���t���Ă��̔n���ɖY����Ȃ��v���o������Ă�ꂽ�͖̂����Ȃ��Ƃ��B
������x���K����������
>>336
�n���Ȃ��O�ɂ͕�����Ȃ����낤�ȁB���ɂ͕�����B >>339
�Ⴄ�ȁB�i�D�ǂ��͖����B >>341
���̐��ʂ��n���̏؋��Ȃ�B
�u����͂��Ⴂ�n���̂��O2����y�̂̋C�����vꏂ��邪�������Ƃ������B�ԈႢ�B >>343
���S�Ȃ銨�Ⴂ�B�n���͊ԈႦ����Ԃł��邱�Ƃɋ�ɂ������Ȃ�����y�ł����� >>352
�n���͂��������v�l������A�Ƃ������{�������Ă���ȁB >>356
�n���ɂ��������o���Ă��Ȃ��Ƃ����A���O�݂����Ȓ�x�����̐l�Ԃ̉������� >>358
�v�l��~�̓T�^�I�ȃ��X�B >>361
�������Ă���B���͏����Ă���B >>363
�O����^��Ȃ̂����������Ă���l�Ԃ��_���I�ȕ��͂��������ނ��Ƃ��ĉ\�Ȃ̂��H
�u�����v�Ƃ������t�ׂĂ��炱�̎���ɓ����� �Ƃ肠�����u�������w��N��b�ł߁v�͔�Ꭾ�ȊO���s������
�ŏ��͂ǂ����悤���Ȃ����炢�����ł��Ȃ��������Ǥ�J��Ԃ�����Ă��炷�炷�������悤�ɂȂ�������
����όp�����đ厖�����
>>376
���̈����l�Ԃ����X��1�̊�b�ł߂Ƃ͂ȏ�
��邾�����ʁA���Ȃ������}�V�̌��{ >>377
�ł��Ȃ����Ƃ��ł���悤�ɂȂ�̂�
��ʓI�ɂ͖��ʂƂ͌���Ȃ� >>378
�u���X�v�܂��ē����Ȃ��ƊԈႢ�B����Ɉ�ʐ���������ȁB
���̔n������1�̊�b�ł߂�����͖̂��ʁB >>379
�ǂ������H�����Y�݂ł�����̂��H�炢���Ƃł����������H
�����Ă�邩�猾���Ă݂ȁB >>380
�݂��Ƃ��Ȃ������v��������w�E����Ď��܂肪������ӋC�����Ėi���Ă邾���̉��z�Ȑl�Ȃ�A�����Ƃ��Ă���� >>382
�������Ƃ��J��Ԃ��n���B
�݂��Ƃ��Ȃ��Ƃ�����������̂͂��̔n�����B�떂�������Ƃ��Ă������� �J��Ԃ������́u��o���������l�ԂƂ͕ʐl�v�Ȃ̂Ŏw�E�����̕���₃�������Ă��Ȃ�
���S�_�j����ĉ������͕̂����邪�����Ȃ�����
>>378
�n���̎��o�𑣂������̂���
���O�͎������n���ł��邱�Ƃ����̎w�E�ɂ�藝���ł������ȁH
����Ƃ��n�������痝���o���ĂȂ����ȁH �ł����l����̏������݂ɒN�����������Ă�̂�����Ȃ���
���Ȏ��������Ă��S�����肪�����Ȃ瓰�X�ƍ\���ăX���[����Ηǂ���ˁH
����I�ł͂Ȃ����_�̔��_���҂����Ă���܂�
>>386
�����Ȏ��������Ă��S�����肪�����Ȃ瓰�X�ƍ\���ăX���[����Ηǂ���ˁH
����́A���O���n�������牴����̔��_������āu�X���[���ė~�����v�Ƃ�����]�B
�ԈႢ��n���̎w�E�����O�ɑj�Q����邱�ƂȂ�(�X���[���邱�ƂȂ�)�A���͎��R�ɏ������ށB >>382
���̃��x���̔n�������ɉ��������Ă���Ƃ��A�X�Q�[�ȂƎv���B���̔n���ɔn���̎��o�������������ˁB >>376
���O�͂����̖����A�~���悤�̂Ȃ��n���B��1�̐��w�Ƃ�����Ă����ʂ������߂Ƃ���
����������1�̐��w����������炢�Ŋ��ŕ��Ȃ��Ă�낵�� >>381
�悵�悵�B������Ȃ��Ă�����B�N�������鈫����͑���ɂ��Ȃ��Ă����B
����͖���������A�Ȃ�ł��b���Ă����B �]��ɓ��̈����l�Ԃ����A���̔n�����C�W���Ă�낤�ƍl�����B�n��������Ă����B
�n���͎������Ȃ��W�I�ɂ��ꂽ�̂������ł����u�����̔������������̋C�ɏ����(�ɂ��Ƃ��������)�̂��v�Ɣn���Ȑ��_�����Ă��邪�I�O��B
��������
>>391
�Ȃ�قǁI�悭���������B�N�͐����ȁI
����Ȍ����N��n���ɂ����Ȃ�Ăق��Ƃ���B �u���͂Ƃ��܂����œ����낤�Ƃ���n���𒆊��`������Œׂ��̂͊y�����B
�ނ���ɂ��Ƃ����˂��ꂽ�牴�͈������ނ�������Ȃ��B�������I�O��ȁA�n���̔��_�͕����Ă����Ȃ���
�n���ɂ͂���2��(�I�m�Ȏw�E�ƓI�O��Ȕn���̎w�E)�̑傫�ȈႢ��������Ȃ��悤���B
��艴�̋C�������S���������ĂȂ�������
������Ȃ��ƌ��������Ă�����
�n���̒P���ȋC�����ȂNJȒP�ɕ�����
�W�J�����Ə�@�������ē������̂ł����H
���_�I�������������������
>>400
>>���_�I�������������������
�u�͂��_�j�v�ƌ����Ă݂����H >>376�ŕ��R�ƃh���Ȏ��������Ƃ��ĕ��R�Ǝ��������ʂ݂����ɑ���̂��Ă�˂�
�����ƕ��̂��肶��˂����e���F�� >>306
����͍P��������Ȃ��̂��H >>400
���_����@�Ƃ����Ɓ@�┄��݂������ȁB >>405
�H
0x=0
(1-1)x=0
x-x=0
x=x >>408
�������͖��Ӗ����ł͂Ȃ��s����i�s���̈ӂł͂Ȃ��s�m��̈Ӂj�ƌ����B�S�Ă̎����������Ɛ���ׁB�����
0x=1
�̗l�ɑS�Ă̎����������Ɛ���Ȃ����s�\�ƌ����
�u�C�ӂ́`�v���ĒP���p�����u�S�Ắ`�v���ĒP���p�����̂͂��̏����w�����s�������X���ɉ�����Ȃ��C�������ס ��1�h�����A���ʐ}�`�̍��ł�
���̕��̐���ɂ�聛�܂���✕��t����ƌ������ł�
(3)���s�ȕ��ʂɁA1�̕��ʂ������ƁA���̌����͕��s�ɂȂ�
����ɂ��āA�Ⴆ�Ε��s�ȕ���A�CB������Ƃ��āA�����ɕ���P�������ꍇ�A������߂̉\��������Ǝv���u✕�v�Ƃ����̂ł����A�����́u���v�ł���
������Ȃ��̂ʼn��̂����Ȃ̂�����܂���
>>413
������P�̏�ɂ���̂ł˂���ł͂Ȃ��B����A, B�̏�ɂ���̂Ō������Ȃ��B�c��͕̂��s�B >>414
���݂܂���A�悭����܂���
���s�Ȗ�A�CB������Ƃ��āA����͐^�����猩����u���v�̗l�ɂȂ��Ă���ƍl���Ă���̂ł����Ⴄ��ł��傤��
�����ɕ���P�������Ƃ��A�Ⴆ�ΐ����Ɍ����u�y�v�̗l�ɂȂ�\���������Ȃ����Ɓc �u�m�v�̂悤�ɂȂ��Ă��Ă��A�����̒��������������A���ʓI����Ȃ��āu���̓I�Ɂv���ڂ���Ε��s�ɂȂ��Ă��܂���B
>>415
�y�̌�����:�̕��������畽�s���Ǝv���܂� >>415
����͖ʓ��m��������Ă��镔���ł͂Ȃ��������m��������Ă��镔�������Ă��܂��Ă��邩��ł��B�y�Ƃ������͖ʂR�ł͂Ȃ����R�{�łł��Ă��܂���ˁB���̌������Ƃނ��땽�s�ɂ͐�ɂȂ�܂���B
�������m��������Ă��镔���ł͂Ȃ��ʓ��m��������Ă��镔�������Ă��������B�Q�{�̒������\��Ă���͂��ł��B���̂Q�{�̒����͕K�����s�ł��B >>414
���w�I�A�[�@�I�ȍl�����H�f���炵���B >>415
��Ԃł̒����̈ʒu�W�́A�܂�����邩�ۂ��ő�ʂ����B�����Ȃ��ꍇ�A2���������ꕽ�ʏ�ɂ���Ε��s�A���ꕽ�ʏ�ɂȂ���˂���B
���̏ꍇ�A����A�Ƃa���2�����͌���邱�Ƃ͂Ȃ��A�Ƃ��ɕ���P��(���ꕽ��)�ɂ���̂ŕ��s�B
>>419
�S�R�A�[�@����Ȃ��B�����̏����@�B >>417-420
�x���Ȃ肷�݂܂���
���������m��������Ă��镔���ł͂Ȃ��ʓ��m��������Ă��镔�������Ă��������B�Q�{�̒������\��Ă���͂��ł��B���̂Q�{�̒����͕K�����s�ł��B
���̐��������ɂ킩��Ղ������ł�
�[�����܂���
���肪�Ƃ��������܂��� >>256
> �u��40�A��37�A�{�l12�A��(�܂��͖�)10�Ζ��v������(����͕����̖��_���܂�)�B
����͉������ȂH >>423
�Ɛg�̐l�����ɑ���z�����Ȃ� �O>>335
>>423
�q�����炢�̏����ɑ��ēG�ӂ������ɂ��Ă���ƎƂ߂�ꂩ�˂Ȃ��B ����c�C�b�^�[���ł悭����t�F�~�j�Y���C���̉ߌ��h�A�ʏ̃c�C�t�F�~����
���܂�ɂ����\�߂��Đ��E�I�ȃt�F�~�j�Y���c�̂��ꌾ��悳���W�c�I��������Ԃ�
���E�I�ȃt�F�~�j�Y���c�̂���No��˂��t����ꂽ�c�C�t�F�~���ɔz������K�v�͖���
���݂܂���A�m���̌v�Z�𐔔N�Ԃ�ɂ��Ă���̂ł����A
����x�̒��I�ŁA�ȉ���5�̒��I�����鎞
A.20%�œ�����
B.5%�œ�����
C.5%�œ�����
D.5%�œ�����
E.1%�œ�����
���̂����A�����ꂩ2�̓������������m�����Ăǂ��v�Z��������ł����H
�NjL
��������������͖߂��O��ł�
��������
2�̓������������m���̋t�����v�Z������@���ȁB
�A���œ�����m���ƃn�Y���̊m��
���Ɍv�Z���āE�E�E�B
P(�S�n�Y��) = (84/100)ⁿ
P(�n�Y����A�݈̂���) = (84/100)ⁿ
�� P(�n�Y����A�݈̂������S�n�Y���ł͂Ȃ�) = (84/100)ⁿ - (84/100)ⁿ
...
�𑫂�
C���č��Z���w�ł�������
�S�R�o���ĂȂ���c
>>433
�}�W�������I
�����̌v�Z�ƑS�R�Ⴄ�ȁA�ǂ����Ă��낤�c >>427
���I��������Ȃ����A2��݂̂Ȃ̂�2��ȏ�Ȃ̂���������Ȃ��̂ŋ��߂��Ȃ��B >>434
�����S�����M�Ȃ��̂ŁB�����Ȃ�v�Z���o�����Ǝv�������ǁB >>427
����������A~�d�����ꂼ��Ɨ�����1���I������Ă��ƁH��������NjL��
>��������������͖߂��O��ł�
�̈Ӗ����ʂ�Ȃ���ˁB >>427
��x�̒��I��5�̒��I�Ƃ��A�NjL�œˑR�������o�Ă�����Ƃ��A���t���悭������Ȃ��B
��蕶���̂܂܂��m�肽���B >>437
���Ȃ݂ɓƗ����I��2����������Ȃ�3.5245% �O>>425
>>427
3(0.2�E0.05�E0.95^2�E0.99)+(0.2�E0.95^3�E0.01)+2(0.8�E0.05^2�E0.95�E0.99)+3(0.8�E0.05�E0.95^2�E0.01)+0.8�E0.95�E0.05^2�E0.99
=0.035245
��3.5245% >>427��2��A�����Ĉ�����A-E���_�u��Ȃ��悤�ɓ�����m�������߂�Ƃ����Ӗ����Ǝv�������LjႤ�̂��I �悭�悭�ǂ��x�̒��I�ł��ď����Ă����
��x�̒��I�œ����Ƃ��Ӗ����������
���肷��K�v�Ȃ���
�Q��ނ̓����肪�_�u���ē�������Ęb����Ȃ��́H
��x�̒��I��ABCDE��5��ނ̂���������������Ƃ��ł���B
���ꂼ��̓���̊m����>>427�B
5��ނ̂����̂������肪��̊m�������߂����B
�Ă��Ƃ��B�������ƒ��g������̂Ŗ���߂��Ƃ������Ă�낤��
�v�����A����̖{������Ȃ��ē���̊m���������Ă���̂Ŋm����
>>427�̂܂ܕς��Ȃ��ƍl���Ă����悩��B
AB����ő��O��AAC����ő��O��A�ȉ����ł��ꂼ��̊m����
���߂������Ȃ����i�Ō�ɍ��Z�j�Ǝv�����B �v���Ƃ��Ȃ�Ƃ���Ȃ̃G�X�p�[�ł���n�Y���Ȃ���
�������^��Ɏv�������A�ǂ�����ɓ`�����炢��������킩���A�z����ɂ��邾������
�܂��܂���
�z���g�͖�蕶���ו��܂ŋL�ڂ��Ă����Έ�Ԃ����ǂˁB
�ł��A�ו��̔F�����Â����Ă̂����̈�A�̂��Ƃ�ł킩��J���W�B
�����͌����Ă��������X��炩������Ȃ�
�݂�ȓlj�͂Ȃ��Ȃ��B���Ԃ������B
�ʏ�U�����A25%�̊m���ŁA�X�L��A�������B25%�̊m���ŁA�X�L��B�������BA��B�͓����ɔ������鎖������B �����������Ȃ��m���A�Е��݂̂���������m���A��Ƃ���������m����m�肽���ł��B
�����ł����ׂ܂������A �S��������܂���ł����B�ǂ̂悤�Ȍv�Z�����s�����A�����Ē����Ȃ��ł��傤���H
>>447
�����ĂȂ����Ƃ�����ɗ\�z���邱�Ƃ�lj�͂Ƃ͌���Ȃ��B �O>>440
>>448
A=0.25
B=0.25
A��B=0.25^2=1/16=0.0625
�PA���PB=0.75^2=(3/4)^2=9/16=0.5625
A���PB=0.25�E0.75=3/16=0.1875
=�PA��B
6.25%+56.25%+18.75%+18.75%=100%
�x���}��`����4�̗̈�ɕ�������B �O>>450
>>448
�����������Ȃ��m��56.25%
�Е��݂̂���������m��18.75+18.75=37.5(%)
��Ƃ���������m��6.25% >>448
�����������Ȃ��m���B
�@���@�X�L��A�����������X�L��B���������Ȃ��m���ƌ�����������B
�@���@75��(0.75) �~ 75��(0.75) �� 56.25��(0.5625)
��Ƃ���������m��
�@���@�X�L��A���������X�L��B����������m���ƌ�����������B
�@���@25��(0.25) �~ 25��(0.25) �� 6.25��(0.0625)
�Е��݂̂���������m���B
�@���@�X�L��A���������X�L��B�͔������Ȃ��A�܂��̓X�L��A�����������X�L��B�͔�������m���ƌ�����������B
�@���@25��(0.25) �~ 75��(0.75) �{ 75��(0.75) �~ 25��(0.25) �� 37.5��(0.375)
�@�ʉ�
�@���@�X�L��A���X�L��B�̏��Ȃ��Ƃ��ǂ��炩�����������X�L��A�ƃX�L��B�̗����͔������Ȃ��m���ƌ�����������B
�@���@100��(1) - 56.25��(0.5625) - 6.25��(0.0625) �� 37.5��(0.375) �����܂���A�T�C�R�����g��������Ȃ�ł����A
�T�C�R��2�ʁX�ɓ�������
�����Ƃ�6���o�Ėڂ̍��v��12�ɂȂ�m����1/36�ł���ˁH
�����ŃT�C�R������2�������ꍇ
�ڂ̍��v��2~12��11���1/11�̊m���ŗ����Ƃ�6�̖ڂ��o��ƂȂ�̂ł���
�m�����ς�����C������̂ł������̂ł��傤���H
����ɂ����Ă����܂���B
>>453
11�ʂ肪�������m���ŏo��킯����Ȃ�����
2��12�͍ł��m�����Ⴍ�Ă��ꂼ��1/36
7���ł��m����������6/36 = 1/6
�������ʁX���͑S�����W �⑫
12��6��6���o�������Ȃ��@���@1/36
7��1��6�ł�2��5�ł�3��4�ł�4��3�ł�5��2�ł�6��1�ł��ǂ��@���@6/36 �� 1/6
>>453
�����ł��ʁX�ł���̖ڂ�
1��1
1��2
~
6��5
6��6
�̂ǂꂩ��36�̑g�����i�ڂ̏o���j������B
�Ⴆ�Ζڂ̍��v��4�ɂȂ�̂�
1��3�A2��2�A3��1��3�ʂ�Ŋm����3/36(=1/12)�B���v��12�ɂȂ�̂�6��6�̈�ʂ�Ŋm����1/36�B ���ŁA�ς��ꌅ�̐��ɂȂ�ꍇ�̂݁u���v������܂��B
�@(�ɂ���u���v�낭�A�@���������u���v�����A�͂�����ɂ��イ�� �Ȃǁj
����͂Ȃ��Ȃ̂ł��傤�H
>>457
�ς��Ȃ�K�� ���イ �����邩��
���イ �̑��� ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂɂ���;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;�ɂ�〜����������;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;/ ���������P/�_;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;/((^o`^�^)) /�u;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;/����' �ҁ܃�/�^|;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖�PUU�҃ҁP‖�@|;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖�@���@�� �@‖�@|;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖________‖�^|;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖�P�P�P�P ‖�@|;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖�@���@���@‖�@|;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;�^‖________‖�^�^|;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;‖�P�P�P�P�P�P�P‖�@|;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;‖�@ �� �@�� �@�� �@‖�@|;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;�^‖_____________‖�^�^|;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;‖�P�P�P�P�P�P�P�P�P‖ �@ |;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;‖�@���@���@���@���@���@‖ �^ |;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;‖ ________________‖ ;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;‖;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;����;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;����;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;(_ _ )�M�܂�;;;;;;;;;;;;;;;;;;;;(_ _ )�M�܂�;;;;;;;;;;;;;;;
;;;;;;;��;;;;;��;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;��;;;;;��;;;;;;;;;;;;;;;;;;;;;;;;
�O>>451 x5��-x4��-1
��������������
�O>>460
>>461
x^5-x^4-1=(x^5-1)-x^4
=(x-1)(x^4+x^3+x^2+x+1)-(x^2)^2
=[��o(x-1)(x^4+x^3+x^2+x+1)�p+x^2][��o(x-1)(x^4+x^3+x^2+x+1)�p-x^2]
=[��o(x-1)(x^4+x^3+x^2+x+1)�p+x^2][4�捪��o(x-1)(x^4+x^3+x^2+x+1)�p+x][4�捪��o(x-1)(x^4+x^3+x^2+x+1)�p-x]
x=0�̂Ƃ��ɑ�l-1,x=4/5�̂Ƃ��ɏ��l-5/4 ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂɂ��������;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂ�ɂ��ɂ��ɂ���;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;�ɂ�〜���͂�������;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;/�P�P ���� ���� �P�P/�_;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;/�@�@ ((^�`^o^)) �@/�u;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;/�@�@ ����' �ҁ܃� �@/�^|;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖ �P�P�PUU�҃ҁP�P ‖�@|;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖ �@���@���@���@�� �@‖�@|;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖�Q�Q�Q�Q�Q�Q�Q�Q‖�^|;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖�P�P�P�P�P�P�P�P‖�@|;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖ �@���@���@���@�� �@‖�@|;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖�Q�Q�Q�Q�Q�Q�Q�Q‖�^|;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖�P�P�P�P�P�P�P�P‖�@|;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;‖ �@���@���@���@�� �@‖�@|;;;;;;;;;;;;;;;
;;;;;;;;;;�^‖�Q�Q�Q�Q�Q�Q�Q�Q‖�^ �^|;;;;;;;;;;;
;;;;;;;;;;‖ �P�P�P�P�P�P�P�P�P�P‖�@|;;;;;;;;;;;
;;;;;;;;;;‖�@�@�� �@�� �@�� �@���@�@‖�@|;;;;;;;;;;;;
;;;;;;;�^‖�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q‖�^ �^|;;;;;;;;
;;;;;‖�P�P�P�P�P�P�P�P�P�P�P�P�P‖�@|;;;;;;;;;
;;;;;‖ �@ �� �@�� �@�� �@�� �@�� �@�� �@‖ �c�~�;;;;;;
;;;;;‖�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q‖��` , `; ;;;;;;
;;;;;‖;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖/U��U�;;;;;;
;;;;;;;;;����;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;����;;;;;;~U U~;;;
;;;;;;;(_ _ )�M�܂�;;;;;;;;;;;;;;;;;;;;;(_ _ )�M�܂�;;;;;;;
;;;;;;;��;;;;;��;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;��;;;;��;;;;;;;;;;;;;;;;;
�O>>463 log_3(6) �� log_4(7) �̑召���f�͂ǂ�����Δ��f�ł��܂���
log_3(6/3)>log_4(6/3)>log_4(7/4).
/�Q/�l�l_/�Q/_�l�l�Q/�Q
/�Q(_^�Q)/�Q/_(�Q)_)_/�Q
/_�i^o^))/�Q/�i^)�@) _/�Q
/_�i_��_)��_/�i_��_)��_/�Q
/��ރ҄�-��ށ�ރ҄�-���/�Q
/�Q�����c�c/�Q�����c�c�Q
/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�O>>464 >>467 ��������I����Ċ����I�ł��B���肪�Ƃ��������܂����B ���@�ނ�͂悭�A�Љ�ɍv���������ƌ��ɂ���B
���@�Ȃ�ł��Љ�̃l�g�E�������E�ɒǂ����ނ��Ƃ��A�Љ�ɍv�����邱�ƂȂ����ŁB
���@�C�W���⌙���点�ŎЉ�ɍv���ł��鋳�t��x���ɂȂ邽�߂ɁA�����ċA��������ł����āA�c�����E�𗠐����킯�ł͂Ȃ��A�S�́����l�Ȃ������B
���@
���@�̂͋A������Ɨ���҂ƌĂꂽ�肵�����A�c���ɍ��Ђ��c�����܂܋A��������@���m�����ꂽ���݂ł́A�Љ�ɍv�����邽�߂ɂނ���A�����邱�Ƃ���������Ă���B
���@���e�����őO�Ȃ̂��鐶���̔����Ƃł���A���ł͕��ʂɋA�����Ă���B
���@
���@�����w��Ȃǂ̓l�g�E���F�肵�����{�l�𓐎B���āA�s���̎ʐ^���ƌ����Ă�܂��Ă���B
���@�����̎ʐ^�́A�W�c�X�g�[�J�[�Ɏg�p�����B
���@�ނ�͏W�c�X�g�[�J�[���A�m�n��Ŏq���������S���S�p�g���[���n�Ə̂��Ă���B
���w�O�N���̐��̋K�����̖��ł��B
[�G]��[�J]��������܂���B[�E]��m��2��-3�A[�I]��(m-1)��2��+1�Ȃ͕̂��������̂ł����A�um�s�ڂ�n��ځv��un�s�ڂ�m��ځv�̋��ߕ���������܂���B
��[�G]��m��2��-(n-1)�A[�J]��(m-1)��2��+n�ł��B[�E]��[�I]�𗘗p���ĉ������ꂾ�Ǝv���܂����A3��n-1�ɂȂ�A+1��+n�ɂȂ�̂͂Ȃ��ł����B�����ōl����̂����Ȃ̂ŋ�̓I�Ȑ��l�������čl�����ق��������ł����B��낵�����肢���܂��B
http://imepic.jp/20220903/483010
http://imepic.jp/20220903/484020 >>473
3��n-1
4��ڂ̂Ƃ�3. �ł�5, 6,7, n��ڂ̂Ƃ��́H
+1��+n
��s�ڂ̂Ƃ�+1. 2,3,4,n�s�ڂ̂Ƃ��́H >>473
1��ڑ�m �s�ɂ� m^2 ������ł�
��������1���閈��1���邩��
n��ڂ܂�n-1�����ʒu�ł�
m^2-(n-1) >>473
1�s�ڑ�n�Ԗڂɂ�
1��ڑ�n-1�Ԗڂ̐��̎�
�܂�2^(n-1)+1������ł���
1�s�����閈��1�������邩��
��m�s�܂�m-1�s�������
2^(n-1)+1+(m-1) ���ꂳ���ו����c���ς���
149
238
567
�ɂ����̂Ƒ����ĂQ�Ŋ����
137
337
777
�ɂȂ邱�Ǝg���������ȒP�����H
���₻��ȊȒP�ł��Ȃ���
���݂܂���A�������Ă�����ėL����ł����܂�������܂���B
>>474����̂����ʂ�������ƁA4���-3�A5���-4�A6���-5������n��ڂ�(n-1)�͗����ł��܂����B����n�s�ڂ�m��ڂ͂ǂ̂悤�ɑ�������炢���ł����B1�s�ڂ�1��ځA2��ځc��(m-1)��2��+1�ɑ����������ł����A2�s�ڂ�1��ڈȍ~�͂ǂ��l�����炢���ł����B>>476����̌����Ă邱�Ƃ��悭������Ȃ��ł��B����͂��Ȃ��Ă��݂܂���B��̓I�Ȑ��l�������A������Œu�������ė������邱�Ƃ͂ł�����ł��傤���B��낵�����肢���܂��B >>478
����Œ肵�Ă݂�B���Ƃ���5��ڂ�1�s�ڂ��킩������2, 3, 4�s�ڂ͂ǂ��Ȃ�H >>479
5��ڂ�1�s�ڂ�17
2�s�ڂ�18(+1)�A3�s�ڂ�19(+2)�A4�s�ڂ�20(+3)�A�����n�s�ڂ�+(n-1)��(m-1)��2��+1+(n-1)������(m-1)��2��+n �Ƃ������Ƃł��傤���B >>478
1��ڂ�n-1�Ԗڂɂ�(n-1)^2�������
������1�s�ڂ�n�Ԗڂɂ�(n-1)^2+1�ł���
m�s��(������m<n)��m-1�s��������
���ꂾ��������(n-1)^2+1+(m-1) >>481
>>482
���肪�Ƃ��������܂��I481����̉������������ł���悤�Ɋ撣��܂��B O�𒆐S�Ƃ��钆�S�p180�x�����̂������`OAB�݂�B
���̌ʏ�ɓ_P���B��AB�Ɣ��aOP�̌�_Q����B
AQ=8�ABQ=5�ɂȂ�܂�OQ:QP=2:1�Ȃ����B���̂Ƃ�OP�����͂����炩�B
������6��2�Ȃ�炵���ł����r�����ǂ��Ȃ�܂��ł����B
�O>>470
>>484
OP=OA=OB=p�Ƃ����ƁA
(64+p^2-4p^2/9)/(2�E8�Ep)=(25+p^2-4p^2/9)/(2�E5�Ep)
5(64+5p^2/9)=8(25+5p^2/9)
64+5p^2/9)=8(5+p^2/9)
64-40=p^2/3
p^2=72
p=6��2
��OP=6��2 >>484
OQ=2k, QP=k �Ƃ����B�~�̔��a��3k �B
���ׂ��̒藝���A8�~5 = k�~5k �B�����k=��8=2��2 �B����ĉ~�̔��a��6��2 �B ��ᔽ���̖���
�u���̌���������S�����̂��̂������
��͏c10�Z���`��20�Z���`�̒����`
������͎R���������̂܂܍Č������`��
�����`�̕��͏d����20�O��������
���̏�������R�����̖ʐς����߂�ɂ͂ǂ�����Ηǂ����H
���ďo�肳��Ă邯�Ǥ�ȂɌ����Ă�̂��S�������ł��Ȃ���N���킩��l����H
�O>>482
>>487
�R�����̌`���ӂ̒����`�Ɂu���ϕό`��������I�v���Ă��Ƃ�����A
�c�̒�����akm�Ƃ����ƁA
a�~2a=4465
2a^2=4465
a=��(4465/2)
=��8930/2
��47.25
2a��94.5
���c47km1/4��94km1/2 �O>>488�����B
���҂��Ƃ��낵�B ���Ă�����Ă镪�ۂň������Ǥ���P�̔�ᔽ���̖��Ȃ̂�
��ᔽ���̉������ł��肢���܂��i������P���ȓ������Ǝv���̂Łj
�R�����̏d�����v���Ă��̕���s���甲�����̂��O���t�Ɏ����̂��ȁH
�R�`���̌`�̓S�̒�ʐςł͂Ȃ��ĎR�`���̖ʐς����߂�́H
��������ˁH
>>493
20g�̒����`����R�`���̌`�ɂȂ��Ă�S�̖ʐς����߂���Ė��
�R�`���S�̏d�����v���Ă��̕���20g�̕�����p��ɂ������̏c���i�c�͕ς��Ȃ����j�̖ʐς��v��Γ����ɂȂ邯��
���ꂪ���Ŕ�ᔽ���̖��ɂȂ�̂��͂킩��Ȃ� ���x���Ȃ�̐ς͏d���ɔ��
�������Ȃ��ʐς͑̐ςɔ��
���Ă��Ƃ���ˁH
���H�O�̓S�͑傫���A�������璷���`�ƎR�������o�����B
�����Ȃ̂ŁA�ʐςƏd���i���邢�͑̐ρj�͔�Ⴗ��Ƃ������Ƃł���B�@
�����`�̖ʐςƏd�����^�����Ă���̂ŁA�R�����̏d���𑪂�Ζʐς��킩��B
>>487
>������͎R���������̂܂܍Č������`��
������āA�R�����̑傫�������̂܂܍Č����Ă���Ǝv���Ă悢�̂��H ���͎R�����ƂȂ��Ă邯�nj��݂����̓S���琡�@�Əd�ʂ�������Ă�
�����`�ƕʂ̉����Ȃ�E���R�^�ł������̂ł����ł�OK�ł���
�J��҂�f�킹�邽�߂Ɋ����Č��̖ʐςƂ��ɂ��Ă�C������
�r���ŎR�`���̖ʐϏo�����Ǝ�Ђ˂��Ă�l�����܂���
k��2�ȏ�̐����̂Ƃ��@(k^2+k-1)^2>3(k+1) �����������̂ł���
�������炵�ĂقƂ�ǖ��炩�Ȃ悤�ɂ��v���̂ł���
�����Ƃ��哹����g�킸�������莦�����Ƃł��܂���
k��2�̎��A
(k*k + k - 1)*(k*k + k - 1)
��(2*2+2-1)*(2*k + 2 - 1)
=(5)*(2k + 1)
= 10k + 5
>>500
���ꤓ������u2��3�v�ɂ��Ă��܂������Ȃ������� >>503
���肪�Ƃ��������܂����B
�P�����������i�K�ɂ������̂ł��� ����̎��̕�����k�ɑ��Ēl���������肵�Ȃ�������Ȃ�Ă��Ă����́H
>>506
���̏ꍇ�͗ǂ���B
����k�ɑ��āA�قȂ�l����ꂽ�肵����_�������� x^3-3x-3=0�̎�������1�����Ȃ����Ƃ�
�����@�ɂ�炸�������Ƃ͖����ł��傤���B
x=2��8-6-3<0������ЂƂ̎�����a��2���傫��
�������O�p��2��̘a��0²-2(-3)=6���a²��菬����
���c��2����2��̘a��0����
�O>>501
>>508
f(x)=x^3-3x-3�Ƃ����ƁA
f'(x)=3x^2-3=0��^����x�́A
x=�}1
f(-1)=-1��0
f(1)=-5��0
f(2)=-1��0
f(2.1)=9.261-6.3-3=-0.039��0
f(2.11)=2.11(4.22+0.211+0.0211)-6.33-3
=4.4521�~2.11-9.33
=8.9042+0.44521+0.044521-9.33
=9.34941+0.044521-9.33
=0.01941+0.044521
=0.063931��0
��x^3-3x-3=0�̉��͂������2.1��x��2.11�ɑ��݂���B >>509
�[�܂肷���B
�O�p�̘a���O�ŁA�ς����Ȃ̂ŁA���̈�� -a ��菬�����B
�Ƃ��낪�A�O�p�̓��a�i=6�j�� 2a^2 �i>8�j��菬�����B
�����B >>508
�����͎g��Ȃ����ǁA���������������Ƃ����Ăѕ����̂����f�����ɑΉ�������̂��Ǝv������A
�����̒��ɂ͂ǂ����Ă������w������l�^���o�Ă����
>>509�A511���O���������̉���3�ł��邱�Ƃ𗘗p���Ă��邵�A
3�̂���2�����f���ł��邱�Ƃ��A�����ĂȂ������Ŏg���Ă���B >>512
�������I
(x-a)(x^2+ax+a^2-3)=0
�ƈ����������āAa>2�ŁA�������̎��������Ȃ��i�����������j���Ƃ����������̂��B
����Ȃ�A���w�͈͂��ȁB �����w���ւ̐����ł悯��A�O���t������Ԃ킩��₷���Ȃ����Ȃ��H

�O>>510
���p�`�� 20���̓ӎO�p�` ABC �ɂ����āC�� AB�CAC ��ɓ_ D,E �����ꂼ���BCD=60 ���C�� CBE=50 ���ƂȂ�悤�ɂƂ�B���̂Ƃ��C�� DEB �͉��x���B
—————————————————————
�}��`���ƁA
��DEB=70�� >>509 �@511 �@513
���肪�Ƃ��������܂��B��͂萔�w�̐l�͂����݂����ł��ˁB
�������L����܂����B >>511
�u�O�p�̘a��0�v���ĉ��H
�p�̈Ӗ����������̂����� 3��������x^3-6x-6=0�̎�������cbrt(2)+cbrt(4)
�ɂȂ�炵���̂ł�������͊ȒP�ɓ�������̂ł��傤��
����ς�J���_�����̌����̍l�������o�R����Ƃ��߂ł��傤���B
���炩�ɏ����w�Z�͈̔͊O���z���ĂȂ�Ȃ�
( (1/(x-1)-1)^3-6(1/(x-1)-1) -6 ) (x-1)^3
= 2-x³ = 0
�̉��̂ЂƂ�³��2
����ė^���̉��̂ЂƂ�
x = 1/(³��2-1)-1
= (2-1)/(³��2-1)-1
= ³��4 + ³��2 + 1 -1
= ³��4 + ³��2
>>521
���p�t�ł����H
����Ȏ����Ȃ�łЂ�߂��̂��A���ɐ������Ă���Ă���낵���Ă�B >>520
���Z�X���ɂ͂��Ă������E����ɂ��ꂸ�C�����X�����Ǝ����������Ȃ����C�ɂȂ�邩��B �R���T�[�g�z�[���ɁA�����8��8���ɂ�����484�l�����ꂵ�܂����B
���̃z�[���̒���͉��l�ł��傤�B
���̖��ŁA�Ȃ��
484/0.88������ƁA������킩��́H�ƌ���ꂽ�B
88%�ɂ����鐔��88%�����邱�ƂŁA�Ȃ�100%�ɂ����鐔���킩��̂��Ƃ����Ӗ��̂悤�ł����A�Ȃ�Ďq���ɋ������炢���ł����H
���̗ǂ������A�����Ă��������B
���ł����̂���
1�F�w��0.84�F484
�܂���
����~0.84��484
������Ƃ��H
>>526
�����A����~0.88=484������@�Ƌ������̂ł����A�����킭�A
484��0.88��1�����킩���āA�����10�{�����Ȃ��́H
484�̒���0.88���������邩������A���������C������B
�ƌ����܂��B
�����͂킩���Ă邯�ǔ[���͂��Ă��Ȃ��Ƃ������Ƃ̂悤�ł��B �P��⁴��2+²��4�����ɂȂ��Ă鎖�����������Ȃ�������ΏI���
������²��2��²��4�̍����鎮��M��͍̂����܂�邩��蔲���ł��Ȃ����̖��
1�ԓT�^�I�Ȏ蔲����
P(x) = (x²+x)^3-6(x²+x) -6
��x=³��2�̂Ƃ�0�ɂȂ鎖�ł����³��2�̍ŏ���������x³-2�ł��鎖����P(x)��x³-2�Ŋ����鎖�Ɠ��l�A����������ł͌|���Ȃ�
�Z�ЂƂg����
²��4+³��2 = ²��4+³��2 + 1 - 1
= ( ³��2³ - 1 )/(³��2-1) -1
= 1/(³��2-1) -1
�ƍl����
Q(x) = (1/(x-1) - 1 )^3-6(1/(x-1)) -6
��x=³��2��0�ɂȂ鎖�Ɠ��l�A���ꕥ���ē���������Q(x)(x-1)³��x³-2�̒萔�{�ƂȂ鎖�Ɠ��l
���ꂪ�������鎖���m�F������j�͂�₨����
>>524
0.88�Ŋ���v�Z�́A88�Ŋ�����100���|����v�Z�Ɠ����B
�S�̂�8��8���ɂ����鐔��88�Ŋ���A�S�̂�1���ɂȂ�B
���̐���100���|����ΑS�̂�10���ɂȂ�B >>527
����Z�̈Ӗ��͕�������܂��BA��B�@���@�`��B�����������邩�Ƃ����̂��P�̈Ӗ��ł����A���ۂ̐l����484�l�ƁA
8��8��=0.88 �̊����Ƃ͑S����ނ��قȂ鐔�ł�����A��������������邩�Ɛ����邱�Ƃ͖��Ӗ��ł��B
�����́A����Z�̕ʂ̈Ӗ��ł���u��鐔���P�ɂȂ������́A����鐔�̑傫�������߂鎮�v�Ƃ����l���𗘗p���܂��B
��X�ɎM���R�����āA���l�Ȋ����ő������Ă���Ƃ��܂��B���R�A��R��������M���P�ɂȂ�܂�����A
�X���R���R���P���R�@�ƂȂ�܂�����A��鐔�̎M�̐����P�ɂȂ������A��������邩�Ƃ����Ӗ��Ŋ���Z�͎g�����ł��B
������ŏ��̖��ɓK�p���܂��B
484��0.8�@�̈Ӗ��́A������0.8���P�ƂȂ����Ƃ��A�l���͉��l�ɂȂ邩�Ƃ������ɂȂ�܂��B�������P�ɂȂ����Ƃ��c�Ƃ����̂�
���̐l��������Ƃ����Ӗ��Ɠ����ł�����A���ɂȂ��Ă��鐔�����߂����ƂɂȂ�܂��B ��ł����@�����邵�A���͓lj����s���u��ׂ���ʁ����������Ƃɂ���ʁv�̌����ɓ��Ă͂߂���@������B
�������ʼn������@������B
���͏��w���̎q�����^��Ɏv�������ɐ^���ʂɌ����������Ă���ɓ����邱�Ƃ���ŁA���ꂪ�M���ɂȂ���Ǝv���B
�ʉ����o���Ă���ł��I�Ƃ����̂͂Ȃ����̕��@���ԈႢ�Ȃ̂������R�Ƃ����������Ƃ������̂��c���Ǝv���B
�܂��A���̖�������������Δ䂪���w�Z�͈͂ň�ԊȒP�Łi�����܂ł���Ă��邩�͒m��Ȃ����j�A�����������ɂ����p���������@���Ɖ����������Ă���B
>>527
���Ƃ������t�̂�����0.1�̂��Ƃ�1(�P��)�Ǝv���Ă�̂���
�ނ��낱��܂ł̊���Z�͂������藝�����Ă�悤�Ɏv���� ���B�������̐l�͉ߋ��X����
���ŕ����̂��Z�͂Ђ�����Ԃ��Ă�����H
�̃X���́u�D�L���v�Ƃ��u�R�c�R�c�����@���B�v�Ƃ�������
���Z�╪���̗����n�m������Ă��l���
�ǂ��Ȃ�H���w�҂ǐ^�ɂȂ�킯�ł��Ȃ���A���������҂␔�w�ȊO�̗��H�w�҂ł���
���Z�╪���̏ڍn�m����K�v�͖����u��{���̊�{�c�[���v�ł��������Ȃ�����Ɋe�w��e������ו��������Ȃ��
����ł��Z�╪�����c���������H���̐l�������Ă��A�������ƕ���A�������H
�����܂Ŋ��S�����ɁA���Z�╪���𗝉�����K�v����̂��ȁH
���Ăł��k���܂ōs���Ȃ��Ə�肭�����w���@�Ƃ́A�ƂĂ��v���Ȃ��
�w�P���n��⌿�ȂǂƉ]�������t�̊T�O�������ꂾ�����o���鎖��
�����ɗ���͂̊g���Ɍq����X�������E�ꋭ�����{��x�Ɉˑ����߂���
�_���\�͂��Ⴂ�܂܁A�w�K�\�͂����͓��{��̓ǂݎ��ɂ�荂���X�������������{�l�ɂ�
���i��ł���Ċw�K���邭�炢�̎������Ȃ��Ɨ���������Ȃ���Ȃ����ȁH
�_�����w���C�������d�x�������āA���ꂪ��肭�s���Ȃ������ɑ��ē������͂ʼn����ė����킯�����
������A��@�R���v���C�A���X�����A�ጛ�@�������̑匴���ɔ�����
�R���v���C�A���X���@���������ނ��A�@���Ō��@�������ނ��鍑�Ȃ��
��@�܂��͈ጛ�ȋ@���̍������߂́A�P�������ł͂Ȃ��A�Ж_��S�����o�������ɂ��߂̗L�������܂鍑�
�w�R���v���C�A���X�����ɂ�鍐���ҕی�̌����x�����݂ɂ����鍑�
>>534
�悭�킩��Ȃ����A������ɂ��敶�͖������ɒ������́A�v�Z�Ƃ͂ǂ��������ɍs���̂���˂��l�߂Ȃ���
���ǐ��w�̒�`���Ɠ����ł������B�����ƂȂ�Ƃ��Ȃ��Ǝv�����B >>524�ł��B
���Ă��������Ă��肪�Ƃ��������܂����I
��Ő������Ă݂���A>>524����̐��������̂܂܂��Ă݂āA>>535����̐��������Ă݂܂����B
�ǂ��܂œ`��邩�ȂƎv���܂������A�[���ł����悤�ł��I
�����̂���Z���̎��_�ŋ�肾�����̂ł��܂�[���l���Ȃ��悤�ɂ��Ă��܂������A�����̎q���ɂ͂����Ɛ������Ă������������̂ŁA�ƂĂ�������܂����B
�O�X���ɕ����̊���Z�i�Ȃ��Ђ�����Ԃ��̂��j
���ڂ��Ă���悤�Ȃ̂ŁA�O�X�������Ă���A��܂��I
�{���ɂ��肪�Ƃ��������܂�😊 ���w�ʼn��̂��l����͓̂N�w�҂̎d���B
�O>>516
JR�̉w�̃z�[���̎��̋@�ɂ���ӂ��̃W���[�X�͂Ȃ������������B�X�g���[�g�����炾�B ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;������{��;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;��������B;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;/�P�P�P ���������P�P�P/�_;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;/�@�@�@((^o`-�-)) �@�@/�u;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;/�@�@�@����' �ҁ܃ҁ@�@/�^|;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;‖�P�P�P�PUU�҃ҁP�P�P‖�@|;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;‖ �@���@���@���@���@�� �@‖�@|;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;‖_________________‖�^|;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;‖ �P�P�P�P�P�P�P�P�P ‖�@|;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;‖ �@���@���@���@���@�� �@‖�@|;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;�^‖_________________‖�^�^|;;;;;;;;;;
;;;;;;;;;;;;;;;;;‖ �P�P�P�P�P�P�P�P�P�P�P ‖�@|;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;‖�@ ���@���@���@�� �@���@�� �@‖�@|;;;;;;;;;;;;;
;;;;;;;;;;;;;�^‖_____________________‖�^�^|;;;;;;;;;;
;;;;;;;;;;;;‖�P�P�P�P�P�P�P�P�P�P�P�P�P�P‖�@|;;;;;;;;;;
;;;;;;;;;;;;‖�@ �� �@�� �@���@�� �@���@�� �@�� �@‖�c�~�;;;;;;;
;;;;;;;;;;;;‖_________________________‖��` , `; ;;;;;;
;;;;;;;;;;;;‖;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;‖/U��U�;;;;;;
;;;;;;;;;����;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;����;;;;;;~U U~;;;
;;;;;;;(_ _ )�M�܂�;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;(_ _ )�M�܂�;;;;;;;;
;;;;;;;��;;;;;��;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;��;;;;��;;;;;;;;;;;;;;;;;;
�O>>516
>>519
f(x)=x^3-6x+6�Ƃ����ƁA
f�f(x)=3x^2-6=0���A
x^2=2
x=�}��2
f(��2)=2��2-6��2-6=-4��2-6=-5.6568�c�c-6=-11.6568�c�c
f(-��2)=-2��2+6��2-6=4��2-6=0.3431�c�c
f(0)=-6
f(1)=-11
f(2)=-10
f(3)=1
f(2.85)=0.049125
���O���t���B���x=2.84�c�c�����݂���Ƃ킩��B �O>>540
2.847322101863073^3-6(2.847322101863073)-6=0 �O>>541
>>543
��BCQ=28㎠
��BPR=��PCS=9㎠
��QSD=5㎠
��ARQ=10㎠
���l�p�`QBCD��9+10+9+12+5=45(㎠)
�ʎl�p�`ABDQ��15+10+��AQD=46(㎠)
��AQD=46-(15+10)=21(㎠)
��21㎠ >>543
����܂�����Ă�B�Ȃ����[�B
����������1998�N�̃����L���O�ɂ܂����O�ڂ��Ă���B >>544
> ��BCQ=28㎠
����͉��łł����H ����A�����Ōv�Z������@17 cm2�ɂȂ����B
�ǂ����Ԉ���Ă��H
�O>>544�C���B�ڑ�������B
>>543
��BCQ=26㎠
��BPR=��PCS=8㎠
��QSD=5㎠
��ARQ=10㎠
���l�p�`QBCD��8+10+8+12+5=43(㎠)
�ʎl�p�`ABDQ��15+10+��AQD=42(㎠)
��AQD=42(15+10)=17(㎠)
��17㎠ >>548
�悭������u�ڑ��v���ď����Ă��邯�ǁA���w�̖��l���鎞�Ɂu�ڑ��v���Ďg���́H �O>>548�C�i�����O���ɖ��O���������Ƃ���ƃR�~�b�N�V�[���A���Ђ炢�ď����Ȃ��B
>>549
��BCQ=��BPR+��PCS+�l�p�`PSQR
=8+8+10
=26(㎠) >>551
��BPR=8���Ă��ƁH
�Ȃ�ŁH �O>>551
>>552
�Ȃ�łƌ����Ă��A���w���ēN�w�Ƃ͈Ⴄ����Ƃ����B m���̕�����A�� m���̕�����B �����E�ɕ��ׂăh�b�L���O����2m���̎��R��AB������́B
����AB���������ɂȂ�悤�ȗ��
�@4��9�̃h�b�L���O 49
�@16��81�̃h�b�L���O1681
�ȊO�ɂ������ς�����܂����B
�Ȃ��A25��00���h�b�L���O����2500�Ƃ����̂̓i�V�ł��B
>>554
���ёO�̃v���O������
m=3
144400 225625 324900
���܂��@����ver4.1
f <- function(x, tol = .Machine$double.eps^0.5){
abs(sqrt(x) - round(sqrt(x))) < tol
}
m=3
n=10^(m-1):(10^m-1)
sqn=n[f(n)]
sqp=as.matrix(expand.grid(sqn,sqn))
sqc=sqp[,1]*10^m+sqp[,2]
sqc[f(sqc)] m=5
5198410000 8122515625 1587624025 3132976729 2528178961 2371690000 6350496100
���͂��ǂ�Ȓl�ł��邩�Ɋւ�炸�A�ł���߂�1�̒l���o�͂��锠�B
��������ƌĂԂ��Ƃ͂ł��܂����H
�em�ɂ��Ă��̂悤�ȕ������͍���Ƃ������Ƃł��イ���H
>>564
����҂ł͂Ȃ��ł����A����Ȋ����ł����̂���
�Em�������̂Ƃ�
1�ʂ�̉������݂���B
m�������Ȃ̂ŁA���ʌ�=a^2 �Ə�ʌ��~10^m=b^2 ��
�Ƃ��ɕ������ƂȂ�A�s�^�S���X���̐�������
a=p^2-q^2, b=2pq, c=p^2+q^2
���� p>q �����݂���B
���̉���
a^2 ��m���Ab^2 ��2m���� 10^m �̔{��
�����藧�̂� p=(1/2)(10^(m/2)), q=p-1 �̂݁B
���̂Ƃ�
m=2, p=5, q=4, c^2=1681
m=4, p=50, q=49, c^2=24019801
m=6, p=500, q=499, c^2=249001998001
�c >>565�̑���
�Em����im=2k+1�j�̂Ƃ�
�������̉������݂��Am��������Ɖ��̌���
������ƍl������B
A=��ʌ��~10^m �ɂ��āA�قړ�����2���̐�
A=PQ �ɕ������ P,Q �����݂��A
���ʌ��̌�� ((1/2)(P-Q))^2 ��
���傤�� m���ƂȂ�悢�B
����T���ꍇ�A���ʌ��͑�������ł͂Ȃ�
��A �ɋ߂�P�A�ς�A�ɂȂ�Q �̑g��
10^k��(1/2)(P-Q)��(��10)(10^k)
�͈̔͂ł����T���悭�A��⍂�����ł���B
���ɂ��F�X�@�������肻��������
�������������܂� m=8�@�ɂ�
2499000199980001
��������Ȃ�
1466124176580001
�������
�����
������ƒ��ׂ�K�v�����肻����
m=1.
49.
m=2.
1681.
m=3.
144400,225625,324900.
m=4.
24019801.
m=5.
1587624025,2371690000,2528178961,3132976729,5198410000,
6350496100,8122515625.
m=6.
249001998001.
m=7.
10547295475600,12232366350400,14042257290000,15976968294400,18036499363600,
23073612250000,25027247420176,36633966760000,48092491265625,58660847767369,
61009002802276,81054099030025,85497762250000,92294449000000.
m=8.
1466124176580001,2499000199980001.
m=9.
102414400506250000,112911876558140625,122478489944332900,123921424612562500,135443044669515625,
140635881210482064,142969849131331600,147476736729000000,160022500791015625,168662169225000000,
173080336855562500,186650244922640625,200732224992250000,203604361605160000,203918400115562500,
246741264139830625,249987721150773841,250019344374190336,293642496166410000,299843856400000000,
316377369659051584,344622096195300625,390655225584672400,399680064226502500,458816400260015625,
468506025625000000,522031104295840000,562543524841928256,571879396525326400,589324176333975625,
656076996201640000,660695616374422500,674648676900000000,736145424417180625,810028521251064025,
815673600462250000,899280144509630625,986965056559322500,999950884603095364.
m=10.
10894620496601400001,24999000019999800001.
m=11.
1023982086478344010000,1232877122522500000000,1256663420152922542401,1330885249690000000000,1384599356142025000000,
1600022606479851456400,1775343056432400000000,1838274988911924640000,1871752334460947265625,2024985920424473473600,
2234068302494084519824,2401012230415575040000,2416439160144100000000,2499972076977969951361,3038781104119712160000,
3039408692143056250000,3156165433657600000000,3164093864177724979264,3317789390465088765625,3751581610024336000000,
3994521876972900000000,4539413748129446560000,4556218320955065315600,4931508490090000000000,5068171587698719754809,
5270743556112825562500,5402277518435043840000,5781812611628476562500,6340172920941127840000,7158728336411316704400,
7353099955647698560000,7724786422519362165904,8099943681697893894400,8441058622554756000000,9370210766422801000000,
9604048921662300160000,9743824680115403292100,9825466393684462890625.
m=12.
249999000001999998000001.
m=13.
10239982771847246325610000,10487971956641822500000000,10556021306259765625000000,10562515630815782774467600,11206297256047190442250000,
11581268025691472824960000,12250018128046706649678400,12369932888042871143858025,14062520810257698960090000,14161666407841082900390625,
14305403867042190400000000,14654530924811737081824256,16000023677448759705702400,16387456182252847656250000,17682004891695716881000000,
18062526729619888886515600,20954733806256942334398561,21381399686446560001562500,21679529256099859600000000,21990991800965104255747600,
22352193542253422500000000,23597936902444100625000000,24999973750446890394001936,25176295836161925156250000,32119414117215581406250000,
32187158700844928400000000,34360924689007975399605625,37903728845441284255562500,38950101220842624400000000,39337962244003008056640625,
40163887526492182119840000,41951887826567290000000000,43810299342816708100000000,46325072102765891299840000,47978390176092250000000000,
50770093812841196836000000,53095358030499226406250000,54635743300414217149744900,56646665631364331601562500,57221615468168761600000000,
58618123699246948327297024,61035184809003340765106176,71402466713763879324160000,77102405998245895791015625,80999949104017995067278025,
85283389902242889575015625,87637727746895904900000000,88073798047292191975003024,96040055350897975117200625.
m=14.
2499999000000199999980000001.
>>565�̔��Ⴊ���������悤�Ȃ̂ŁA�C������
���̉���
a^2 ��m���Ab^2 ��2m���� 10^m �̔{��
�����藧�̂�
(1/(2��2))(10^(m/2))��p��(1/2)(10^(m/2)),
q=p-1 �̂Ƃ��B
�i�������Ap���ő�̂Ƃ��K�����藧�j
�Ƃ���
3535��p��5000, 35355��p��50000, ...
�͈̔͂ŕʉ����Ȃ����m���߂�Ηǂ������ł�
�v���O�����̐l������������
m=8, p=4376, q=4375, c^2=1466124176580001
m=10, p=40625, q=40624, c^2=10894620496601400001
�Ƃ��Ă���Ɋ܂܂�܂� �l�p�����ŁA4�̑��ʂ������ȎO�p�`�Ȃ�A���̎l�p������
�@��ʂ������`�ŁA4�̑��ʂ͍����ȓӎO�p�`
�ɂȂ�Ƃ����܂����B
���݂܂���B�����ł��ˁB����Ȃ͂�ꂢ������܂����B
���݂܂���B�ł͂��炽�߂�
�l�p�����ŁA4�̑��ʂ������ȎO�p�`�Ȃ�A
���̎l�p�����̒�ʂ͂Ђ��`�Ƃ����܂����H
>>572
������ 500/��2 �łȂ�
500/(2.5^(1/4))��397.6353�c
�ł悢�ł��傤 >>575
����Ƃ��āA�ƂȂ荇��2�ӂ���������
4�ӂ��������Ȃ��u�����`�v�ƂȂ�ꍇ������܂�
�l�p���� H-ABCD �ɂ�����
AB��BC��HD, CD��DA��HB, HA��HC
�Ƃ���A��ʂ� AB��BC �̂����`��
���ʂ�4�̎O�p�`�͍����ɂȂ�܂� ���肪�Ƃ��������܂������B
�ׂ傤�ɂȂ�܂����I
�E���摜�Ȃ�ł����킩��܂���B
�������������͈̔͂��ǂ������B

>>584
�O�p���ŃS�����������25�ɂȂ���
���ꂢ�Ȑ��ɂȂ����̂ł��܂����@������̂����m��Ȃ� �u���[�̎l�p�`�ɂ����āA�����C���̕��̑Ίp���������ƁA
�����͐��O�p�`(�Ȍ�T1)�A�㕔�͑S�̂Ƒ����̎O�p�`(�Ȍ�T2)�ɂȂ�B
�ʐ�8�̎O�p�`(�Ȍ�T3)�̎O�ӂ��@6a,6a,6b
�ʐ�15�̎O�p�`(�Ȍ�T4)�̎O�ӂ��@6a,6a,6c
�Ƃ���ƁA�S�̂̎O�p�`�̎O�ӂ́@8b+4c,4b+8c,12a�@�ƕ\����
T2�ɂ����āA60���̊p����Εӂɐ����������ƁA
T2�́AT3�̔����Ƒ����̐}�`�ƁAT4�̔����Ƒ����̐}�`�ɕ������A
������𗘗p���đΕӂ̕Ӓ��Ɋւ��鎮�����ƁA3a^2=b^2+c^2+bc�@�Ƃ�������������B
(���̎��͗]���藝������o���邪�A��̂悤�ɂ���ƒ��w���w�ł��o����)
���Ƃ́AT3�AT4�̖ʐς̎������A�A��������ƁAa,b,c�����܂�A�w�����Ȃǂ���S�̖̂ʐς�48�Ɖ���A
����Ă��镔���̖ʐς�25�ƕ�����B
�ȏ�A�͋Z�ł��B�X�}�[�g�ȕ��@�����肻���łȂ�܂���B
>>587
�Ȃɂ���H
�����>>586���y�ɉ������H
������u���w���ɂ��킩�邯�ǂ������ē����v����Ȃ���H �}�̂悤�ȕ⏕�����l����B�����AE=a�CAD=b�Ƃ���
OB=OD=OE=OC ������AO�𒆐S�Ƃ���Ɠ_B,D,E,C�͓���~����ɂ���B���������ā�BDC=��CEB=90��
��A=60���Ȃ̂� AC=2b�CAB=2a
��BEC=�Q��OEC=30=��3a�~(2b-2a) �C��BDC=2��BDO=16=��3b�~(2a-b)
��͂�����A���������a,b���v�Z�ł��邩��A������o���ā�ABC�S�̖̂ʐς���8��15�������Ί���
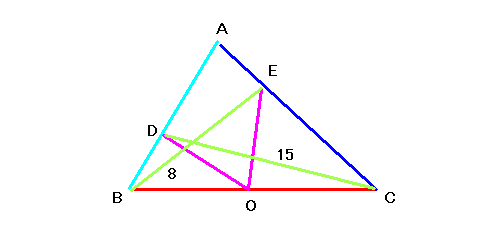
�m�~�L�b�N�O�p��
�}�̎O�p�`�̏�A���A�E�̒��_��A,B,C�Ƃ���
BC�̒��_��D�Ƃ��ԎO�p�`����BDF�A�ΎO�p�`����CDE�Ƃ���CDE = 2x, ��BDF = 2y�Ƃ���
x+y = ��/3�Ɓ�CDE : ��BDF = 15:8�ɂ��
15:8 = sin(2x):sin(2y)
= sin(2x) : ��3/2 cos(2x) + 1/2sin(2x)
�� 15:1 = sin(2x) : ��3cos(2x)
t = tan(x)�Ƃ����
2t : ��3(1-t²) = 15:1
������t = 5/9��3 ( �� t > 0 )
�� ��CDE : ��DEF = sin(2x) : sin(��/3)
= 15/26��3 : ��3/2
= 15 : 13
�� ��CDE = 15/13��DEF�A��BDF = 8/13��DEF�A��FBCE = 36/13��DEF
��AEF : ��AEF + ��FBCE = 1:4��聢AFE = 12/13��DEF
>>590
�ł�T1�����O�p�`�Ƃ͌��܂��ĂȂ��悤�ȁc �������ɂ��̖��ŏo�Ă���12�����̊p�x��x,y�ŕ\���̂͂ł��Ȃ��Ƃ܂����̂ł͂Ȃ�����
�����ĉ������B
���鏬�w���̖��ŁA�l���Ă���r���ŁA
���~����16129�@�́������߂�K�v�������肪����܂����B
�܂胋�[�g16129���o���Ȃ��Ɛ�ɐi�߂Ȃ��Ƃ������Ƃł��B
���w���Ȃ�16129�������������ē����������m�̃y�A������Ċe�y�A�̕Е����|�����킹��
���[�g�̓�����Ƃ����������ɂȂ�Ǝv���̂ł����A16129�͖��炿���ƌ������܂���B
�������2�ł͊���Ȃ��Ȃ��B3�ł��������i�e���̐����𑫂��Ă�3�̔{������Ȃ��j�B5�ł͖��������A
7�ł�����Ȃ��݂������B�M�Z���Ă݂�����11�ł������Ȃ��̂��킩�����B���l��13�ł��������Ƃ킩�����B
����A����M�Z����Ċm���߂Ȃ��Ⴞ�߂Ȃ낤�B�������₾�B
��
�����Ȃ��Ă��܂��܂��B�e�̎��������ƌv�Z�@�ł���Ă݂���127�ł����B
�q�ǂ�������127�ɒH������@�������ĉ������B���̍쐬�҂��u���\����M�Z����Ă��127�܂ł����͂��v�Ƃ�
�z�肵�ĂȂ��Ǝv����ł��B
16129�̃��[�g�����w���ł��v�Z�ł�����@���Ăǂ����������ł��傤�H
�������ł��邱�Ƃ��킩���Ă��邩��A100*100���傫���A200*200���͏������A�݂����ɍi�荞��ł����̂��ȂƎv���܂�
>>595
�|�����킹��1�̈ʂ�9�Ȃ̂ŁA���Ƃ�1�̈ʂ�3�~3��7�~7
100�~100��10000�A110�~110��12100�A120�~120��14400�A130�~130��16900
120��130�̊Ԃ�1�̈ʂ�3��7
123�~123�A127�~127���v�Z
10000��100�~100�Ƃ������ƂɋC���t���A10���i20���ł��������ǁj���₵��
�|�����킹�݂�A���������|�����킹���Ƃ���1�̈ʂ�����Ƃ̐���1�̈ʂ�
���������� ���肪�Ƃ��������܂����I�I
�Ȃ�قǁB
�u������2��ł���v�Ƃ����O�������q���g�ł������ł��ˁB
�E�������͈͂����߂Ă����B
�E1�̈ʂ����Č����i��
�ꐶ���̒m�b���C�����܂��I
�]�菬�w���������ᖳ����������Ȃ����ǁA130^2=16900�����\�߂��ƌ������ƂɋC�Â����Ȃ�A
(130-x)(130+x)=130^2-x^2=16900-16129=771=3*257=(130-127)*(130+127)
�Ƃ���127�������邱�Ƃ��ł���B
�̉c�Ƃ���Ă��Ƃ��Ԃ̃i���o�[127�ł����B�Ȃ�ǂ����̂����B���̂��яC�����āA�y�����o�������������B�Ō�͎�����āA�Ă�������������Ă���Ԃɓ˂�����ł���ꂽ�炵���āA�p�ԂɂȂ������āB����Ȑ�������A127�́B
��Ԃł��A�i�q�_�݂̂_�Ƃ��鑽�ʑ�(���݂������)�̑̐ς͗L�����ɂȂ�܂����H
����ł�����낵�����˂������܂��B
�����l�ʑ̂̑̐ς��L�����Ȃ���Ȃ�
determinant�ő̐όv�Z�ł������
AD��BC�����s�ȑ�`ABCD�Ƃ��܂��B
��AB��ɓ_P�A��DC��ɓ_Q���AAQ��PC�����s�Ȃ�悤�ɂƂ�ƁB
���̂Ƃ��}�����낢�돑���Ă݂�ƁADP��QB�����s�ɂȂ肻���Ȃ̂ł����A
����͐������ł����B
>>603
�͂��A���藧���܂�
�ؖ����@�́A���Ƃ���
ABCD�����s�l�ӌ`�łȂ��Ƃ�
AB��DC����������_��O�Ƃ���
AD//BC, AQ//PC
����OAQ�Ɓ�OPC������
���ӂ̔���v�Z
����OPD�Ɓ�OBQ������
��PD//BQ
�̂悤�ɂ��܂� >>604
��炪�x���Ȃ�܂����B
���肪�Ƃ��������܂��I�I (x⁵-x⁴-1)/(x²-x+1) = x³-x-1
(x^2 - x + 1) (x^3 - x - 1)
>>606
���w���x���łǂ�����H ��낵�����肢�������܂��B��֒��������̂������Ղ̊ȒP�Ȗ�肾�����ł��B
���j�@�艿400�~�A����250�~�̏��i��100�d����܂����B�͂��ߒ艿�Ŕ���A�r������S�����Ŕ������Ƃ���
�艿�Ŕ������Ƃ����Q�{�̌�������܂����B����ł��܂�����c���Ă����̂ł�������1��100�~�Ŕ���A
�Ō�܂Ŏc����10�͎̂Ă܂����B�ŏI�I��4400�~�̑��ł����B�@100�~�Ŕ��������͂����ł��傤�H
��
���̖��ɂ��Ẳ�����������ł��܂���B
(�菇1)���������z����A�S�̂̔���z�͏o����
�@�@250*100-4400=20600�@���@20600�~�����ゾ�B
(�菇2)�艿�Ŕ��������ƂS�����Ŕ��������̂��ꂼ��͏o���K�v�͂Ȃ��B
�@���̗����̐��̍��v�̌��A�艿�ƂS�����̕��ςŔ������ƍl���Ă����B
�@�@�i400*1+240*2�j��3��880/3 ��880/3�~�Ŕ������̂��B
(�菇3)���ꂽ�̂�90���Ƃ����_�ɒ��ڂ��Ă邩�ߎZ�œ������o�邼�I
�@�@(880/3*90-20600�j��(880/3-100)��30�@��30���I
��
����3�i�K�ڂ��܂������킩��܂���B�菇1�Ǝ菇2�͂Ȃ�قǂƗ����ł��Ă܂��B
���̗����ł́A
�艿�Ŕ����������`�A4�����Ŕ����������a�A100�~�Ŕ����������b�Ƃ���ƁA
A+B+C=90
880/3 * (A+B) + 100*C = 20600
�ƂȂ�܂��B�ŁAC�̐����o�����߂ɂǂ����ď�L(3)�̎��ɂȂ�̂������ł��܂���B
������C��0���Ƃ��Čv�Z���Ă݂āA������i880/3-100�j�Ŋ�����ĉ��̂���Ȃ̂��B�B
���������i880/3-100�j���ĉ��Ȃ̂��B�B�����ς�ł��B
�킩��₷��������Ă��������B
>>610
�邩�ߎZ���ď�����Ă邶���
���ꂽ90�S����880/3�~�Ŕ����Ă����Ƃ���ƍ��v880/3*90�i�~�j
���ۂ̔���z��20600�~�����炻�̍���(880/3*90-20600�j�~
880/3�~����100�~��1����ւ����880/3-100�i�~�j����グ������
������ւ���Ηǂ����v�Z���鎮��(880/3*90-20600�j��(880/3-100)�Ōv�Z�����30�i�j
30����ւ���Ǝ��ۂ̔���グ�ƍ����Ȃ��Ȃ�̂�30��100�~�Ŕ������� �i�j�����Z���̖��

���݂̗��������@�̏������(����100���~�ȏ�)�̔N��15%�ł�
��������邩�H >>611
���肪�Ƃ��������܂����I�X�g�����D�ɗ����܂����B >>612
�����s���œ�����2����ˁB �O>>553
>>584
���߂�ʐς�S�Ƃ���ƑS�̖̂ʐς́A
15+8+S=S+23
60���̒��p�O�p�`�̎O�ӂ�2��5,4��5,2��15
45���̒��p�O�p�`�̎O�ӂ�2��15,2��15,2��30������A
2��5�~2��15�~1/2-8(2-��3)+(S+23)�o��30/(2��5+2��15)�p^2=S
10��3-16+8��3+(S+23)15(2-��3)/4=S
4(18��3-16)+15(2-��3)S+345(2-��3)=4S
72��3-64+26S-15S��3+690-345��3=0
(15��3-26)S=626-273��3
S=(626-273��3)(26-15��3)
=16276+12285-(7098+9390)��3
=28561-16488��3
=2.9462848�c�c
(�v�Z�ԈႢ���Ă�\��������)
�}��`����23���炢�B
��23 �O>>617
>>584
�ʐϔ�͑�����̓�悾����A
1:4=S-x^2��3:S
S-(8+15+S)/4=x^2��3/4
4S-23-S=x^2��3
3S=23+x^2��3
sin��:sin(120��-��)=8:15
15sin��=8(sin120��cos��-cos120��sin��)
15sin��=8(cos�Ɓ�3/2+sin��/2)
15sin��=4cos�Ɓ�3+4sin��
11sin��=4cos�Ɓ�3
121sin^2��=48cos^2��
121-121cos^2��=48cos^2��
cos^2��=121/169
cos��=11/13
sin��=4��3/13
(x^2/2)sin��=8
x^2sin��=16
x^2=16/sin��=16�~13/4��3
x^2��3=4�~13=52
3S=23+52=75
��S=75/3=25 �搶���A���肢���܂��B
���w�̖��ŁA���̎��ɂȂ镶�͑�����Ƃ�����肪�o�܂����B
100x+150(60-x)=1900
���ꂪ�o���Ȃ������̂ł����A�ǂ����������͑�ɂȂ�Ηǂ������̂ł��傤���B
�ǂȂ��������Ă��������B
>>620
1��100�~�̃~�J����1��150�~�̃����S�����킹��60�������Ƃ���A�����1900�~�������B�~�J���͉��������H >>621
�����������ȂƂ͎v������ł����A�����Ȃ��x��142�ɂȂ��Ĉ�a�������Ȃ��̂ł����A����Ȃ��̂ł��傤���H
������60�Ȃ̂ɁA142���āI�I���ĂȂ��āA�Ⴄ�̂����Ǝv���Ă����玞�Ԑ�ŏ������ɏI���܂����c�B >>622
���Ⴀ
1��100�~�Ŏd���ꂽ�����S��1��150�~�Ŕ���A60����c���Ă���i�K��1900�~�̐Ԏ����o�Ă���B���d���ꂽ�H 60�~�ŋ肵��150����������100�����Ĕ����߂�����
�c��������1900�~�������B���̊����́H
�O>>618�C���B
>>584
�ʐϔ�͑�����̓�悾����A
���߂�ʐς�S�Ƃ���ƁA
�ӎO�p�`�̓��ӁV�̒�����x�Ƃ��āA
1:4=S-x^2��3/4:S+8+15
4S-x^2��3=S+23
3S=23+x^2��3
�Ԑ��Ɛ��̐ړ_�����Ԑ����̒�����x�Ȃ�A
��p���Ăꂱ��2�{���ĎO�p�`�S�̂ɂȂ�B
�ʐ�8�̐Ԃ��ӎO�p�`�̒��p���ƂƂ���ƁA
sin��:sin(120��-��)=8:15
15sin��=8(sin120��cos��-cos120��sin��)
15sin��=8(cos�Ɓ�3/2+sin��/2)
15sin��=4cos�Ɓ�3+4sin��
11sin��=4cos�Ɓ�3
121sin^2��=48cos^2��
121-121cos^2��=48cos^2��
cos^2��=121/169
cos��=11/13
sin��=4��3/13
�ʐ�8�̐Ԃ��ӎO�p�`�ɂ��āA
(x^2/2)sin��=8
x^2sin��=16
x^2=16/sin��=16�~13/4��3
x^2��3=4�~13=52
3S�̎���x^2��3�̒l��������ƁA
3S=23+52=75
��S=75/3=25 3�����̊i�q�_�Ńs�b�N�̒藝�݂����Ȓ藝���Ă���܂���
�G���n�[�g�������̗��_�Ƃ��߂�����
a,b��1�ȏ�̎��R���B
a�~b = 2^(a-b)
�����Ƃ��Aa,b�����߂�
x = �}2^(3/4)
�������͒m���
(a,b)=(-1,-2),(-1,-1),(1,1),(2,1)
>>630
�����B��������
>>631
����ȊO�������Ƃ��ؖ����Ȃ��Ƃ� >>631
628���Ă���̂��Ƃ�����A
�w1�ȏ�́x���R�����ĕ������ǂ߂Ȃ��̂��ƌ��������B
�������������w���Ń}�C�i�X����Ă����� �O>>625
>>628
2^2=4,2^4=16,2^6=64,2^8=256�c�c
2�̋������2�̔{���̓��̂悤���B
a=2,b=1,ab=2
2^(2-1)=2
��a=2,b=1 �O>>634�����B
>>628
a=2,b=1�̂Ƃ�ab=2
2^(2-1)=2^1=2
a=1,b=1�̂Ƃ�ab=1
2^(1-1)=2^0=1 ����
�Q�[�����ʉ݁u�R�C���v���ăv���C����Q�[��������̂ł���
�ȑO��97%off 17000�R�C��/ 610�~�Ƃ������[�g�Ŕ����Ă����R�C�����A������98%off 28000�R�C��/ 1600�~�ƒl�グ����܂����B�����̒l�グ�ɂȂ����ł��傤��
��낵�����肢���܂�
�N�������w�܂ł̐��w�͈ËL�Ȗڂƌ����Ă���l���m���ɂ������ȂƎv���̂ł����A�݂Ȃ���͂ǂ��v���܂���
> (1600/28000)/(1-0.98) / ((610/17000)/(1-0.97))
[1] 2.388759
>>640
2.388�{������138.8%�̒l�グ�Ə����邩�ȁB >>641
Tnx
10������AppStore��3���l�グ�ɂȂ��Ă�̂ł܂��܂��Ó��Ƃ����Ƃ���ł����A�������ǁc �O>>635
>>636
2.459-1=1.459�c�c
����14��5��9�Ђ̒l�グ ����A�킩��܂���
�����ĉ�����
�A�D�R�@�C�D�S�@�E�D�T�@�G�D�Q
�O>>643
>>646
�E��5����Ȃ����Ȃ��B
����Ėł��鐔���͓�����ւ���B �O>>648�Â��B
>>646
�A/�C+4/3=�G+1/12
(�A,�C,�G)=(2,3,4)�̂Ƃ�2/3+4/3=2��4+1/12
=(4,3,2)�̂Ƃ�4/3+4/3=8/3��2+1/12
=(3,2,4)�̂Ƃ�3/2+4/3=17/6��4+1/12
=(3,4,2)�̂Ƃ�3/4+4/3=25/12=2+1/12
��(�A,�C,�E,�G)=(3,4,5,2) CF�aBD�@�Ȃ̂Ł@��BDF = ��BDC�@�ȉ��������Ł@(3*3/2)/2=9/4
�O>>649
>>650
�v�Z�ʼn��������ϕό`���邩�B
(��1)CE=EF=t�Ƃ����ƁA
��BEF�ɂ����ăs�^�S���X�̒藝���A
(3/��2+t)^2+t^2=3^2
9/2+3t��2+2t^2=9
2t^2+3t��2-9/2=0
4t^2+6t��2-9=0
t=�o-3��2+��(18+36)�p/4
=3(��6-��2)/4
=3cos75��
BE=3sin75��
��BFD�͒��p30���̓ӎO�p�`������A
��BFD=2��BEF=BE�EEF
=�o3(��6+��2)/4�p�o3(��6-��2)/4�p
=9(6-2)/16
=9/4
=2.25(㎠)
(��2)
BD//CF������A
��BFD�Ɓ�BCD�ɂ��āA
���BD�ɑ��鍂���͂Ƃ���3/2
����BFD=��BCD=(1/2)3(3/2)=9/4=2.25(㎠) ��낵�����肢���܂��B���w�����̖��ł��B

A���~�̒��S�Ƃ��܂��BAC��3cm�AAB��6cm�Ƃ���ƁA���̉~�̖ʐς́H�Ƃ������ł��B
���̉������ł����A�܂��A
�@�u�~�̔��a�A�܂�AD�̒�����������Ή����邼�v�Ǝv�����A������
�@�u�O�p�`ABD��DAC�͑����ŁA�������2:1���B������CD:AD:BD��1:2:4���v�ƋC�Â��āA
�@�uDC��①cm�AAD��②cm�ƍl���Ă݂悤�B�����BD��④cm�ɂȂ邼�v
�@�u�i④+①)�~②��2��9������A①��1.8cm���ƕ����������v
�Ɛi��ł����Ƃ��܂��B
���̑����Ȃ�ł����A�J
�i�l����X�j
�@①=1.8cm������AAD=②=3.6cm���B
�@������A�~�̖ʐς́A3.6�~3.6�~3.14�ŁA40.6944���I
�i�l����Y�j
�@①=1.8cm������AAD�~AD=②�~②=④=1.8�~4=7.2���I
�@������A�~�̖ʐς́A7.2�~3.14�ŁA22.608���I
�@
��2�ʂ�̍l���������āAY�̕��������ł����B
X�̍l�����̉����_���Ȃ�ł��傤���H �A�͇@☓2�ŇC�͇@☓4�Ȃ̂�
(�C+�@)�~�A��2��9�@�́@(�@☓4+�@)☓(�@☓2)=10☓�@☓�@=18�@������@�@☓�@=1.8
�~�̖ʐ�=�A☓�A☓3.14=�@☓�@☓4☓3.14=1.8☓4☓3.14=7.2☓3.14
�l����X�ł������LJ@���Ⴄ�̂ō���Ȃ�
�l����Y�͂��܂��܍����Ă������Ł@AD�~AD=�A�~�A=�C�@�͊ԈႢ
AD�~AD=�A☓�A=(�@☓2)☓(�@☓2)=�@☓�@☓4�ł����ćC�Ƃ͈Ⴄ
������������C�ƌ�F���Ă�̂ŋ��R����������
���aAD���w�Ƃ��Ăc�b���o���āE�E�E�E�B
①��1.8���ǂ����ă_���Ȃ̂��A�ڍׂɋ����Ă��������B
�ǂ��l����ׂ��������̂��B
>>655����ɂ��ƁA
�E�l������X�Ő����AY�̓_��
�E���������O���①=1.8���Ԉ���Ă邩��AX�ł����ʂ̓_���AY�̌��ʂ����Ȃ̂͋��R�Ȃ���
�Ƃ������Ƃł���ˁB
�ǂ�����①=1.8���_���Ȃ�ł��傤�H �i④+①�j�~②��2��⑩�@���@����_���ł����H
④+①��⑤�@���@�����OK���Ǝv���܂��B
⑤�~②��⑩�@���@����ɉ�����肪�����ł��傤���H
①�Ƃ�②�Ƃ��������������Ȃ��ŁA
①��a���Ƃ��āA②=2a�̂悤�ɍl����ׂ��Ȃ̂ł��傤���H
���Ȃ��Ƃ��A�����Z������Ƃ��͂������ׂ����Ǝ��i���w���j�ɒf�����ċ����Ė��Ȃ��ł��傤���H
>>662
BD��④��DC��①�Ȃ�BC��⑤�A�Ƃ��������ł��B >>665
�i④+①�j�~②��⑤�~②��⑩�@�ł��B �D�~�A���I�ƒ�`�����̂ł���·D�~�A���I�Ə����Ė��Ȃ���
>>667
��`�Ƃ����悤�Ȃ��̂ł͂Ȃ��ł��B
�����m�̂Ƃ���A���w���͔�ŕ\�킷���߂�①��②���g���̂ł����A
�����łłĂ���⑤�~②��⑩�Ƃ��������ł��B�������5�~2��10�ɏ����Ă������������ł��B
���ꂪ�_���������ł��傤���H
�������ɁA⑤�~2��⑩�@�Ȃǂ͂悭�g�����ǁA�@⑤�~②�Ȃǂ̂悤�Ȏg�����͂������ƂȂ���������Ȃ��ł��B �D�~�A���I�Ƃ����̂ł���·D�~�A���I�Ə����Ė��Ȃ���
>>669
���߂�Ȃ����B⑤�~②��⑩�Ɓ@�u�����v�@�킯�ł͂Ȃ��ł��B
�g�������Ƃ��Ă���C�����Ĕ߂����ł��B�����Ă��������B
���\�킷���߂́��l���݂��ɂ����Z����̂��_���Ƃ��������ł�낵���ł��傤���H ���Ȃ������Ȃ�́H
���₳��Ă��������Ă���������悤�ɂ͓������܂���B
�����n���ōU�߂��Ă���C���������ł����ł��B
���Ɖ����|�����̂�����Ȃ��`���Ή����|���悤�Ə��肶��Ȃ��́H
�Ȃ�őʖڂ��Ǝv�����̂���������Ȃ�
�����炾���ǁA����ȃL�c�C����������ĂȂ������c�c
>>661
��Ⴗ�钷����①�Ƃ�②�Ƃ�⑤�Ƃ��ŕ\���̂́A��ɏm�̎�@�ł��ˁB���ʂ̌������w�Z���t���֗�������g���l�������ł���
�����������ȏ��ɍڂ��Ă��Ȃ�����ȁ[
>�i④+①�j�~②��2��⑩�@���@����_���ł����H
>④+①��⑤�@���@�����OK���Ǝv���܂��B
>⑤�~②��⑩�@���@����ɉ�����肪�����ł��傤���H
��ԏ�ƈ�ԉ�����肪����܂��B��̒����͑����Z�����Z�͂ł��܂����A�|���Z�͒ʏ�͐��藧���Ȃ�����ł��B
�����@�̏c����̒�����①�ʼn���②�ɂȂ�܂���ˁB����Ɩʐς́A��̊|���Z���ł���Ȃ�①�~②��②�ɂȂ�܂��B
�Ƃ��낪①=3cm�Ƃ����Ƃ��܂��傤�B�����②=6cm^2 �ɂȂ�܂����A�{���̖ʐς�3�~6=18cm^2 �ƂȂ��č����܂���B >>675
����̒����͑����Z�����Z�͂ł��܂����A�|���Z�͒ʏ�͐��藧���Ȃ�����ł�
���肪�Ƃ��������܂����I
�������肵�܂����B ����̊|���Z���ł���Ȃ�@�~�A���A�ɂȂ�܂��B
���łɂ��̎��_�œ�̎��ɂ��������Ȃ��̂œ�l�̉�b�ɂ��Ă��Ȃ���
����ȓ�̎�������Ȃ藝���ł��Ă��܂����_�ŕςȍl���������ݕt���Ă��܂��Ă��œƎ��̕\�L�@�͎~�߂ċ��ȏ��ʂ�Ɋw����������
>>653
�R�~�U���Q���i�T�^�Q�j�`�c�~�`�c���Q
�P�W���i�T�^�Q�j�`�c�O�Q
�`�c�O�Q���R�U�^�T�@�i�`�c���U�^��T�j
���������ĉ~�̖ʐς͂R�U�^�T
�ꌩ�A�Q���������������K�v������Ǝv�킹�Ƃ���
���͂���ȕK�v���Ȃ��āA�`�c�̒��������߂�����
�`�c�O�Q����ʐς����߂���Ƃ������ɌƑ��Ȗ��
�������ǁA����Ȃ�����Ă����w�҂ɂ͂Ȃ���
���w�҂ɂȂ���������ۏ��邗���� >>653
���uDC���@cm�AAD���Acm�ƍl���Ă݂悤�B�����BD�͇Ccm�ɂȂ邼�v
�@AD=2DC�ABD��4DC�A���Ă��Ƃł��ˁ@���̒ʂ�ł��B
���u�i�C+�@)�~�A��2��9������A�@��1.8cm���ƕ����������v
�@�TDC�~�QDC���Q=9�ł��B�܂�TDC�O�Q���X�ł��B
�@���Ȃ��̏������ł����ƂT�i�@�~�@�j���X�ł��B
�@������@�~�@���P�D�W�icm^2)�ł��B
�@�ł��@�́�P�D�W��1.3416407����@�ł��B
�@�܁A�������@�����߂�K�v�͂Ȃ���ł���
�@�@�~�@�����߂������ł����� >>681
���A���ł�>>655�œ������Ǝw�E���Ă܂����ˁB
�܁A�Z�����������킩���Ă���A�N�ł������邱�Ƃł�����B >>661
���i�C+�@�j�~�A��2���I�@���@����_���ł����H
�@�_���ł�
�@�n�����J�ɏ�����
�@�i�@�{�@�{�@�{�@�{�@�j�~�i�@�{�@�j���Q
���i�@�~�@�j�{���(10��)����{�i�@�~�@�j���Q
�@���Ă��Ƃł�
�@�����Łu�@�~�@�́A�@�łȂ��v�i>>660�j�Ƃ������Ƃł�
���D�~�A���I�@���@����ɉ�����肪�����ł��傤���H
�@�͂��A�Ԉ���Ă܂�
�@�D�~�A���i�@�~�@�j�{���(10��)����{�i�@�~�@�j�ł�����
�@�@�~�@�͌����ć@�ł͂���܂���
�E�E�E�Ă��Ƃ��A����������Ă܂��˂� >>670
���i�D�~�A���I�́j�������5�~2��10�ɏ����Ă������������ł��B
�����ꂪ�_���������ł��傤���H
�@����
���D�~2���I�@�Ȃǂ͂悭�g�����ǁA�@
���D�~�A�Ȃǂ̂悤�Ȏg�����͂������ƂȂ���������Ȃ��ł��B
�@�����ł��傤�@����Ȏg�����͂ł��Ȃ��ł�����
�@�D�~�Q���I�A�͂����ł����A
�@�D�~�A���I�A�̓_�����Ă��Ƃł�
�@�@�~�@���@�@�ł͂Ȃ�����ł�
�@�����ƒ����̐ς͖ʐςł����āA�����ł͂Ȃ��ł���H >>670
�����\�킷���߂́��l���݂��ɂ����Z����̂��_��
���Ƃ��������ł�낵���ł��傤���H
�@�������A�_���ł����A�Ȃ��_�������A���Ȃ��͗������܂������H
�@���l�̌��t����������邾���ł͔n���̂܂܂ł���
�@���R�͊��ɏ������Ƃ���
�u�����ƒ����̐ς͖ʐςł����āA�����ł͂Ȃ��v
�@����ł�
�@�����Z�ł͓����P�ʂ̂��̂𑫂����킹�܂�
�@�������|���Z�͂����ł͂���܂���
�@�P�܂Q����َ̉q���T�܂ʼn��A�Ƃ����ꍇ
�@�Q�͑܂̒��َ̉q�̌��ŁA�T�܂͑܂̐��ł�
�@�܂�P�ʂ��قȂ�܂��@
�@����͎Z���ɂ������b�ł���
�@�w�Z�ł͐M�����Ȃ��قǕ̂�ɂ���Ă��܂�
�@�����炭���t���S�R�������ĂȂ���ł��傤
�@���ɒQ���킵�����Ƃł� ���ʐς́A��̊|���Z���ł���Ȃ�@�~�A���A�ɂȂ�܂��B
�@�ł��܂��ǂ�
�@�Ȃ��A���������������Ȃ��̂ł��傤
�@�K�v�Ȏ�Ԃ��T�{�邩��n���ȊԈႢ�����ł����̂ł�
�@�@�~�i�@�{�@�j���@�~�@�{�@�~�@
�@����ȏ�͂ł��܂���
�@�A���Q�~�@�Ƃ����Ƃ���ŁA���ǂ͓������Ƃł�
�@���~a�́Aa^2�ł�����a�ł͂Ȃ��̂ł�
�@���Z�̐��w�T�ł͓�����O�̂��Ƃł����A
�@���w�Z�Ńn���p�ɓ�������ƃE�\�v�Z���ĊԈႢ�܂�
�@�@�~�@�͇@�ł͂Ȃ��@�䂦��
�@�A�~�B��6�~�i�@�~�@�j�ł����ćE�ł͂Ȃ�
�@���ꂪ�̐S�ł���
�O>>656
>>688
��ABC:�l�p�`CHEF=�l�p�`CHDF=1:(2+3)=1:5 ��BAC=��ADE�����p���������̂�BA��DE�͕��s
��ABD�Ɓ�EDF�A��BDA�Ɓ�DFE�����ꂼ�ꓯ�ʊp�ɂ�蓙������ABD�Ɓ�EDF�͑���
�䂦��FE��ED�͓��ӂ�EF=ED=AC�@AC��EF�͕��s����������AEFC�͕��s�l�ӌ`
BA��EF�̉������̌�_��P�AF��ʂ�BA�Ƃ̕��s����AC�̌�_��Q�Ƃ���
���p����PAE=��DEA�@
�����ā�PEA=180-��DEF-��DEA=180-��BAD-��PAE=��DAE
�����AE�����L����̂Ł�DAE=��PEA
��APFQ�́�APED��4�܂݁�APED�́�DAE��2�܂ނ̂Ł�APFQ�́�ABC��8�܂�
GC��DE�̌�_��R�Ƃ����AG:DR=AC:DC=3:2
AG:ER=AG:DE-DR=AG:3AG-2/3*AG=3:7
��AGH�Ɓ�ERH��3:7�̑���������GH:HR=3:7
GR:GC=AD:AC=1:3������GH:GC=3/10:3=1:10
��AGH=1/10*��AGC=1/10:��ABC
��AHC=��AGC-��AGH=��ABC-��1/10*��ABC=9/10*��ABC
��CHEF=��APFQ-��APE-��FQC-��AHC=��ABC(8-1-1-6/10)=54/10*��ABC
��ABC:��CHEF=5:27
��BAC=��ADE�����p���������̂�BA��DE�͕��s
��ABD�Ɓ�EDF�A��BDA�Ɓ�DFE�����ꂼ�ꓯ�ʊp�ɂ�蓙������ABD�Ɓ�EDF�͑���
�䂦��FE��ED�͓��ӂ�EF=ED=AC�@AC��EF�͕��s����������AEFC�͕��s�l�ӌ`
BA��EF�̉������̌�_��P�AF��ʂ�BA�Ƃ̕��s����AC�̌�_��Q�Ƃ���
���p����PAE=��DEA�@
�����ā�PEA=180-��DEF-��DEA=180-��BAD-��PAE=��DAE
�����AE�����L����̂Ł�DAE=��PEA
��APFQ�́�APED��4�܂݁�APED�́�DAE��2�܂ނ̂Ł�APFQ�́�ABC��8�܂�
GC��DE�̌�_��R�Ƃ����AG:DR=AC:DC=3:2
AG:ER=AG:DE-DR=AG:3AG-2/3*AG=3:7
��AGH�Ɓ�ERH��3:7�̑���������GH:HR=3:7
GR:GC=AD:AC=1:3������GH:GC=3/10:3=1:10
��AGH=1/10*��AGC=1/10:��ABC
��AHC=��AGC-��AGH=��ABC-��1/10*��ABC=9/10*��ABC
��CHEF=��APFQ-��APE-��FQC-��AHC=��ABC(8-1-1-9/10)=51/10*��ABC
��ABC:��CHEF=10:51
�O>>689
>>688
��BAC=90���ɕ`���ƁA
BA=1�Ƃ���AC=3,BC=��10
��ABC=3/2
GC��BF�̌�_��M�Ƃ���ƁA
G���N�_�Ƀ��l���E�X�̒藝���A
(GB/BA)(AD/DC)(CM/MG)=1
(2/1)(1/2)(CM/MG)=1
(CM/MG)=1
����BF�͌X��-1�ŕ`����B
��CHEF=12-3��ABC+��HGA
=12-3(3/2)+��ABC/10
=(3/2)(8-3+1/10)
=(3/2)(5+1/10)
=(3/2)(51/10)
=��ABC(51/10)
����ABC:��CHEF=10:51 ��낵�����肢���܂�
A(b+c+d)Z=AbZ+AcZ+AdZ
����͊ԈႢ�ł͂Ȃ��ł��傤���H
b�Ac�Ad���ꂼ��ɑ��đO��A��t������Z��t�������Ƃ����ŕ\�������ł�
>>695
���ȉ������܂���
�X���������炵�܂��� >>668
�������ˎ����Œ�`���q�ׂ��Ȃ��\�L�@���g�����Ƃ��ʖڂ��� �@���Z�@�A���Z�{�Z�@�B���Z�{�Z�{�Z�@����@�Ɓu��`�v����
���̂Ƃ��A�Ⴆ�·@�{�C���D�ƂȂ�
����@�~�@���@�Ƃ͂����Ȃ��@
�Ȃ��Ȃ�i�Z�~�Z�j���Z�Ȃ�āu�ؖ��v���ĂȂ�����
�܂�A�~�B�́i�Z�~�Z�j�{����i�U�j����{�i�Z�~�Z�j�ł����Ȃ�
�����ćE�A���Ȃ킿�Z�{����i�U�j����{�Z�Ƃ͂ł��Ȃ�
��⚪︎���Q�����B
�i(���~��)
��(______�j
��⚪︎���Q�����B
�i(���~��)
��(______�j
�s�p�O�p�`�̏W������݊p�O�p�`�̏W���ւ̑S�P�˂��đ��݂��܂����H
���̎O�p�̒���D�ƕ��s�Ȓ�����_A�Ɠ_B�ɏ����ꍇ
�R���p�X�ƒ�K�����g���ď����ɂ͂ǂ�������ǂ��������Ă���

�����Ȃ��ǖ��ɐ���{�����Y�ꂽ�����ł܂����₵����
�{���͒���D�ɐ�������������Ăāu����̌�_O�����ɂ��đΏ̈ړ������}��������v���Ė��Ȃ̂�
�悭�͂킩��Ȃ߂��Ⴍ����ȒP�����Ȗ�肾�ȁB
>>705
���������}���ׂ��́u���Ώ̂Ɉړ������_�v�ł����āA�uD�̕��s���v�ł͂Ȃ���B ������������������肩�珑������

�O�p�`�̓_A�B�C��D�����ɂ��đΏ̈ړ���������Ė��Ȃ��ǂ�
�_A�B�C��D�ɐ����ŕ��s�Ȓ������180�x��]������ΑΏ̈ړ��������ɂȂ�̂͂킩�����

���̕��s�Ȓ����x��Ȃ��ŃR���p�X�ƒ�K�����ň����̂��킩��Ȃ��킯
�ςȂƂ���ɍS���Ă�̂͂킩�邪��킩��l�������狳���Ă��� ���ꂼ��̓_����~�������āu���̉���������~�������Č�����������180�x�̈ʒu�v���Ď��ł���H����́u���̉������v���킩��Ȃ���
>>708
����A�����畽�s���Ȃ���Ȃ����āB
����D��ɔC�ӂ�2�_���Ƃ�A���ꂼ��𒆐S�ɂ��ē_A��ʂ�~�������āA���Α��Ō�������_�ɂ�A`�ɂȂ�B(���������ۂɂ͉~�܂ŏ����Ȃ��Ă���_���������OK) >>710
���[���������ӂ��ɂ�������悭�킩�����椂��肪�Ƃ��������܂��� �O�p�`�̕ӂ̒����̑g��(a,b,c)�ɑ��ĂR�̐��̐�(s-a,s-b,s-c) (������s = (a+b+c)/2) ��Ή��t����ϊ��ɂȂ��O���Ă��L�������ł����ǂǂȂ����m��܂���H
����������͌���80���Ԏc�Ƃ��܂����B
60���Ԃ܂ł�1.25�{�A����ȏ��1.5�{�ł��B
�Œ����1000�~�œ����Ă����Ƃ��A����������̎c�Ƒ�͂�����ɂȂ�ł��傤
�v�Z���������Ȃ���
>>710
����D�ɔC�ӂ�2�_�������ē_A����~�ʂ������ƂȂ�180�ǂ̈ʒu�Ō�_�ɂȂ�̂��s�v�c�� �O>>701
>>713
60�~1250+20�~1500=75000+30000
=105000
���c�Ƒ��105,000�~ >>716
�ꉞ���P�ł͂�������ĕ`�����l�p�`�̓^�R�`�ɂȂ�A�^�R�`�͑Ίp���������Ɍ���邩��ƒ����I�ɐ�������Ă��� �C�ӂ�2�_��pq�Ƃ���Ɓ�pqA�Ɓ�pqA'�������B
����ĊpApq=A'pq�ƂȂ�A����D�͓ӎO�p�`pAA'�̒��p�̓����A�܂�AA'�𐂒��ɓ�����B
��D�ɐ����ȓ_A�̓�_�̍��W���ďc���͈Ⴄ���lj����̍��W�͋��ʂ����炩
��������
�q�ǂ�����l����B�i���Ȃ��Ƃ��j��l�͒j�ʼnΗj���ɐ��܂ꂽ�B
��l�Ƃ��j�ł���m���́H
�i�u�Ηj���Ɂv���Ȃ������ꍇ�̊m�������߂Ă��������j
P(2�l�Ƃ��j�ŏ��Ȃ��Ƃ�1�l���Ηj�����܂�)
= 1/4 - 9/49 = 13/196
P(�Ηj�����܂�̒j�̎q�Ə��̎q)
= 2�~1/14�~1/2 = 1/14
P( 2�l�Ƃ��j | �Ηj�����܂�̒j�̎q��1�l)
= 13/196/(13/196+1/14)
= 13/27
>>720
��������
�����ǂ��l�p�`����邩�͏����Ă��Ȃ��� ���P���x���Ȃ�P���v�Z�ʼn��Ƃ��Ȃ肻��
�Ǐi�lj��؋����j�Ƃ������t��m�����̂̓i�j�����Z���̋����搶�i�O�{�����j�̘b�ł������B
�����w�Z�ł��؋�������ɂ��ċ��炷������搶�̂悤�Ȗڂɍ��킸�ɂ��ނƎv���B
�y���z
����C�OFX�Ǝ҂ł�
���o���b�W1000(1�h���̏o����1000�h���̎�����\�j�ł���B
����̂P���b�g��10���h���i����100�h���̏o�����K�v�j
�؋����ێ�����20%�����ɂȂ�Ƌ������X�J�b�g�ŏo������S�z�����B
1�h��148�~��1���b�g(10���h���j�����Ƃɂ���B
�ב։����143�~�܂ʼn��������Ƃ��ɋ������X�J�b�g������邽�߂�
���~�o�����Ă����悢���v�Z����B
���A�m��Ȃ��p��̓l�b�g�Ō������Čv�Z���Ȃ����B
��F
�؋����ێ������L���؋������K�v�؋����~100
�L���؋����Ƃ́A����Ŏ��ۂɎg�����Ƃ��ł���؋����̑��z�B
�K�v�؋����́A����ɍۂ��A�P�ʉ݂�����̕K�v�ȏ؋����̂��Ƃ��w���܂��B
>>723
�O��
�Z���̊�b�F���Đ�����
1 �j �j �� ��
2 �� �j �� ��
3 �j �� �� ��
4 �� �� �� ��
5 �j �j �� ��
6 �� �j �� ��
....
191 �j �� �� �y
192 �� �� �� �y
193 �j �j �y �y
194 �� �j �y �y
195 �j �� �y �y
196 �� �� �y �y
> gender=c('�j','��')
> DOW=c('��','��','��','��','��','��','�y')
> dat=expand.grid(gender,gender,DOW,DOW)
> �Βj=\(x)�@(x[1]=='�j'&x[3]=='��')||(x[2]=='�j'&x[4]=='��')
> TueMan=dat[apply(dat,1,�Βj),]
> �j�j=\(x) (x[1]=='�j') & (x[2]=='�j')
> ManMan=TueMan[apply(TueMan,1,�j�j),]
> (nrow(ManMan) / nrow(TueMan)) |> fractions()
[1] 13/27 �㔼
> �j�L=\(x) x[1]=='�j' || x[2]=='�j'
> boy=dat[apply(dat,1,�j�L),]
> boyboy=boy[apply(boy,1,�j�j),]
> nrow(boyboy)/nrow(boy) |> fractions()
[1] 1/3
���p���
�q�ǂ�����l����B
�i���Ȃ��Ƃ��j��l�͓y�j�������j���ɐ��܂ꂽ�B
�i���Ȃ��Ƃ��j��l�͒j�ł���B
��l���j�Ə��ł���m����
�O>>718
>>732
�q�ǂ�����l���ď��Ȃ��Ƃ���l�͒j������A
������l���y�j���ɐ��܂�Ă悤�����j���ɐ��܂�Ă悤�����̐l��1/2�̊m���Œj�ł���A1/2�̊m���ŏ��ł���B
����l���j�Ə��ł���m����1/2 ���Ȃ��Ƃ���l�͒j���y���ɐ��܂ꂽ�ꍇ���܂ށA���ݒ�B
�@�Z�ƒ킪���ɒj�ł���A���Ȃ��Ƃ���l���y�����܂�̊m���@
1/4*(1-(5/7)^2)=1/4*(49-25)/49=6/49
�A�Z�݂̂��j�ł���A�Z���y�����܂�̊m���@1/4*2/7=1/14
�B��݂̂��j�ł���A�킪�y�����܂�̊m���@�A�Ɠ���������1/14
�@
(�A+�B)/(�@+�A+�B)=(1/7)/(1/7+6/49)=7/(7+6)=7/13
>>733
�j�����l���Ȃ��ꍇ��
�@�Z��Ƃ��j�ł���m���@�A�Z�̂ݒj�ł���m���@�B��̂ݒj�ł���m��
�̂ǂ��1/4������@(�A+�B)/(�@+�A+�B)=(1/4+1/4)/(1/4+1/4+1/4)=2/3 >>734
�����y�����܂�ŁA����������j�i�j���͖��W�j�ł��B ���W���
�q�ǂ����R�l����B
�i���Ȃ��Ƃ��j��l�͓y�j�������j���ɐ��܂ꂽ�B
�i���Ȃ��Ƃ��j��l�͏��ł���B
���̂R�l�̒��ɉ��l�������邩�A���̊��Ғl�����߂�B
�O>>733
>>739
��l�͏��̎q�Ƃ킩���Ă��āA
�c���l�̂������̎q�̊��Ғl�͈�l������A
1+1=2
��2�l �P�O�O����̃V�~�����[�V��������
> table(fem)
fem
1 2 3
428368 428700 142932
> mean(fem)
[1] 1.714564
���܂��@R���� ver4.1
# simulation
sim=\(){
girl=sum(sample(0:1,3, replace=TRUE)) # 1:girl 0:boy
DOW=sample(1:7,3, replace=TRUE) # Day of Week 1:Sunday, 2:Saturday
flg <- girl>0 & sum(DOW<3)>0 # flg: one girl at least & one at least kid born on weekend
while(!flg){
girl=sum(sample(0:1,3, replace=TRUE))
DOW=sample(1:7,3, replace=TRUE)
flg <- girl>0 & sum(DOW<3)>0
}
return(girl)
}
fem=replicate(1e6,sim())
table(fem)
mean(fem)
���W���p���
�q�ǂ����R�l����B
�i���Ȃ��Ƃ��j��l�͓y�j�������j���ɐ��܂ꂽ�B
�i���Ȃ��Ƃ��j��l�͏��ł���B
(1)���̂R�l�̒��ɉ��l�������邩�A���̊��Ғl�����߂�B
(2)�R�l�Ƃ����ł���m�������߂�B
(3)1�ڂ̏�����
�@�@�i���Ȃ��Ƃ��j��l�͓��j���ɐ��܂ꂽ
�Ƃ����Ƃ��́A���̐��̊��Ғl�@�Ɓ@3�l�Ƃ����ł���m�������߂�B
>>741
�O�l�Z��̂�������n�l�̊m��p(n)��C[3,n]/2^3
�O�l�̂����N�����y�����܂�̊m����q�Ƃ���Ə����t�����Ғl��
(1*qp(1)+2*qp(2)+3*qp(3))/(qp(1)+qp(2)+qp(3))
=(1*3+2*3+3*1)/(3+3+1)=12/7=1.7142857�E�E�E���܂��̗������������ˁH
���������S���Ӗ����Ȃ������� �����Ŏ��₵�悤�Ƃ����������ȉ����������珑���Ȃ��Đ���������
�A�r�W�W�C���X����ȂƂ���ɗN���Ă���
���ς�炸��t����]����҂��ăo�J�ɂ���邾���������
�܂��ǂ��������ł��������낤��
���a12�Z���`�ʐ�60�����Z���`�̐�`�̊p�x�����߂�����ĉ�����
>>747
���w�Z�Ȃ�47.77��
���w�Z�Ȃ�Ε���150��
�ǂ������ˁH >>743
���_�l12/7�Ƌߎ����Ă��邩�炨�������Ȃ��Ǝv�����B
> mean(fem)
[1] 1.714564 >>745
�A�r�Ƃ͐E��������Ȃ���Ï]���ҁ��A�r���܂���W�̈����e��ł���B��ŁA���̐E��́H >131
���̑z����ƈ�v
�y���ɐ��܂ꂽ���������鎞
������1,2,3�l�̊m��
147/508 63/127 109/508=0.2893701 0.4960630 0.2145669
�����̐l���̊��Ғl
489/254=1.925197
���j�ɐ��܂ꂽ���オ���鎞
������1,2,3�l�̊m��
147/547 273/547 127/547 = 0.2687386 0.4990859 0.2321755
�����̐l���̊��Ғl
1074/547=1.963437
�y���ɐ��܂ꂽ���A���j�ɐ��܂ꂽ���̏����̈Ⴂ�Ŋ��Ғl�ɍ����ł�̂��A���̒����ɂ͔����ċC�����������B
���������ݒ�ɂ���ƁA3�����̊m�������Ғl���j�������ɂ͉e�����Ȃ��̂́A�����ɍ��v������ǁB
�q�ǂ����R�l����B
�i���Ȃ��Ƃ��j��l�͓y�j�������j���ɐ��܂ꂽ�B
�i���Ȃ��Ƃ��j��l�͏����ł���B
>>749
�ߎ����Ă�ƌ����邽�߂̊�͉��ł����H >>750
�A�r�W�W�C�͔]����҂�ԏ�ł��Ȃ��A���^�̂��Ƃ���
�����ł��}�̓I�̂悤����w ���p������2�ӂ�9cm��5cm�̒��p�O�p�`�̑傫�����̉s�p���A�A���p������2�ӂ�7cm��2cm�̒��p�O�p�`�̑傫�����̉s�p���C�Ƃ���Ƃ��A�A�ƃC�̘a�����߂�B
�Ƃ������A�O�p����g���ΊȒP�ɏo����A���w���p�̖��ȂB
���w���͂ǂ�����ĉ����H
>>754
O(0,0), A(2,0), B(7,0), C(7,9),D(0,7)
�Ƃ��ā�ACD�����p�ӎO�p�` >>752
���l�݂����Ɍ덷5%�Ƃ�1%�����ł�����Ȃ��́H >>756
�}���`���ɂ���������W�Ő������Ă邾�����H >>756
�}���`���ɂ���������W�Ő������Ă邾�����H �����`ABCD��AB=9,BC=7�Ǝ��
AB��2:7�ɓ�������_��E,BC��2:5�ɓ�������_��F�Ƃ���
��AED �� ��BFE�ɂ�聢DEF�����p�ӎO�p�`
����EFD = 45��
>>753
�����͓������B
���M���҂�����Ɩh�앞�𒅂ĉ@�O�Ō��̍̎悵�ăR���i�̍R�������B���������l���Ċ��҂̔w���A�������猟�̍̎�B
�A�����m�F���ĉ@���ɓ���Đf�@�B���@�ɂȂ��PCR�����B
1���Ԉȏ�ɗ]���ɂ�����B�挎�͍R�������ŋU�A�����������B
�܂�36�T�C�N�����炢��PCR�z���̔��肾��������E�C���X�ʂƂ��Ă͏��Ȃ������Ǝv���BPCR�����̓J�[�g���b�W�Ɍ��̂����ăZ�b�g���邾���Ȃ̂Ō����Z�t���Ă��ɂł���B �E��������Ȃ���Ï]���ҁ��A�r���܂���W�����̍̎悵����
�^�C�[�z�Č����낤�ȁB�a�@�ɂ���Ă͊Ō�t�����̍̎悵�Ă���Ƃ�������邯�ǁA�����͈�t�̋Ɩ��ɂȂ��Ă���B
�����Ȃ�Ɖ��O�ł̌��̍̎�͑�ρB
>>757
p�l�ƌ덷�͑S���Ӗ����Ⴂ�܂���
���Ȃ��̂����Ő��肵���Ƃ��̒l�̐^�Ƃ̌덷�̕��z�A���Ғl�A���U�͉��ł����H >>748
60���~144�~ X/360 �ŋ��߂�����150���� >>757
���덷5%�Ƃ�1%�����ł�����Ȃ��́H
�Ⴆ�Ώc��10����10�ł��鐳���`�̖ʐς���ꂽ�Ƃ���
95����105�̊Ԃ̐����āu�ߎ����Ă�̂Ŗ��Ȃ��v���Đ^��Ŏ咣������ ���ᓚ���́}5%�ɓ���悢�Ƃ�������
>>750
�A���J���ĂȂ��̂Ɋ�^���Ԃɂ��Ĕ������Ăđ�
�����̂��ƔA�r�W�W�C���Ă悭�������Ă��w >>765
���Ⴀ�A������Ȃ���Ȃ��H >>769
��ŁA���̐E��́H
�Տ��l�^�F���Ȃ̂Ɉ�Ï]���҂Ƃ�������
�A�r���܂���W����H >>771
���w���Ă��Ƃ��ł��Ȃ��V�]���҂͂���������
�����w���ɂ��o�J�ɂ���Ă邼w >>770
��肠��܂���̂Ł@�}5���ȓ���������Ȃ�(�د�@�Ǝ��M�����Ď咣���ĉ����� �ߑO���͐V���@�̂Q�l�A�~�}�ԂP���1.5�@�g�Q�b�g�B
1��͏c�u�C��̏ǗႾ�����B�������Ȃ��o�C�^������Ȃ̂�Boerhaav�͔ے�I�B80�㏗���̏c�u�C��̌o���͏��߂āB
�c�u�C�����������COVID-19�̒v�����͍����@�Ƃ����y�[�p�[�����邩��v���ӂƎv�������A�R���APCR�Ƃ��A���������B
>>773
�V�~�����[�V�����𑝂₵�čs���Η��_�l�ɋ߂Â�������Ȃ��Ǝv���ˁB���Ԃ������邩�炵�Ȃ����ǁB
���_�l�̌��ɂ͗L�p�Ȃ̂ŕp�p���Ă���B
�������Ȃ��Ƃ��͑�������̃v���O������g�ށB >>773
�V�~�����[�V�����𑝂₵�čs���Η��_�l�ɋ߂Â�������Ȃ��Ǝv���ˁB���Ԃ������邩�炵�Ȃ����ǁB
���_�l�̌��ɂ͗L�p�Ȃ̂ŕp�p���Ă���B
�������Ȃ��Ƃ��͑�������̃v���O������g�ށB >>775
���₹�Η��_�l�ɋ߂Â�����}5���̐��x�Ŗ��Ȃ��Ƃ��郍�W�b�N���Ӗ��s���ł� >>763
1000��̃V�~�����[�V�����ŕ��ϒl�����߂�A�Ƃ����̂�1000��s���ĕ��ϒl��1000���߂�E�Ƃ���B
> summary(E)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.641 1.700 1.714 1.714 1.729 1.786
> mean(E)�@#���ϒl
[1] 1.714053
> var(E) #���U
[1] 0.0004643966
> sd(E) #�W����
[1] 0.02154986
���z��

�i���S�Ɍ��藝���琳�K���z�ɂȂ��Ă���͂��j >>774
������t�m���Ă��ł���ˁ[
�ł�Boerhaave�nj�Q�ł����A�c�Ow >>778
���̂����Ł@���̊m�����x���@f(x)=1/(��(1+x^2))�@�̕��ςƕ��U�����߂ĉ����� �O>>740
>>754
sin��(�A+�C)=280/(9��37�E��53)
����(�A+�C)��135.36����135.37�����炢�B >>779
precordial catch �nj�Q�Ƃ��{�����z�����a���ӕʐf�f�ɏグ���B
����͉摜�f�f�ł͊m��ł��Ȃ����B >>777
�Q�O��ɂP��̃~�X�͋��e����̂�Fisher�搶�̂��l�� >>780
�R�[�V�[���z
�܂�Ȃ� >>783
����͗L�Ӑ����̘b�Ō덷�̘b�Ƃ͑S���W�Ȃ���
�덷5%�̘b�ƗL�Ӑ���5%�̘b�͑S���Ӗ����Ⴄ
���Ƃ�����̎����
���₹�Η��_�l�ɋ߂Â����}5���̌덷�Ŗ��Ȃ�
�Ƃ������W�b�N���Ӗ��s�����Ƃ����b����
�]�X���ǂ��q����́H �C�ӂ̊m�����x���ɏ]���������v���O�����Ŕ���������Ε��ς╪�U���v�Z�ł���B
�ݐϖ��x���̋t��������āi�������ł��Ȃ����Ƃ������̂Ńj���[�g���@�Ő��l�����o������j
����Ɉ�l���z������^������̊m�����x���ɏ]�������������邱�Ƃ��ł���B
Neuman�@�ō�邱�Ƃ��\�����ǂ���́A�������闐�������߂邱�Ƃ��ł��Ȃ��̂����_
���
���~�̌`�������m�����x�� f(x) = (2/��)*��(1-x^2)�@�ɏ]��������10000����������
�q�X�g�O������`�悵�ĕ��ρA���U�A�W���������߂Ȃ����B

> summary(y)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.998 -0.404 0.000 0.000 0.404 0.998
> mean(y)
[1] -2.1568e-09
> var(y)
[1] 0.25002
> sd(y)
[1] 0.50002
�\���ɋߎ����Ă���̂ŁAFisher�搶�̂��������ł����B >>785
�𑝂₵����덷������̂łT�������e����Fisher�搶���j�b�R�����Ă��ƁB �������闐����
��
�������闐���̌���
>>787
�L�Ӑ�����5%�Ɛ��l�v�Z�ɂ�����ߎ��̌덷5%�͈Ӗ����Ⴄ ���ς╪�U���o�������Ȃ琔�l�ϕ�����
> pdf=\(x) 2/pi*sqrt(1-x^2)
> integrate(pdf,-1,1)
1 with absolute error < 6.4e-10
> mu=integrate(\(x) x*pdf(x),-1,1) |> print()
0 with absolute error < 4.7e-15
> mu=mu$value
> integrate(\(x)(x-mu)^2*pdf(x),-1,1)
0.25 with absolute error < 5.6e-09
�łł邪�A
���̕��z�ɏ]��������������͖̂ʓ|�B
C����ŏ����Ǝ����ŗݐϖ��x���̋t��������Ĉ�l�������甭�������邱�ƂɂȂ�B
���̓_�AR�̓v���O���������̕��z�̗����͍���Ă����̂Ŋy�B
>>789
�T�������Ȃ�A���܂������Ƃ͂ǂ��ł������A�Ƃ����͓̂�������Ȃ��́H >>782
�]����҂͂��A�肭������ �덷�͈̔́A�댯���ǂ�����A���܂������Ƃɂ͖ڂ��҂�@�Ƃ����_�ŋ��ʁB
��ӂ̎��S�f�f���͋����̂̐����������āA�߂��`�J�`�J�����@�_�A粁A�V�ȂǁB
�����ɂ��َ��̂�����̂Ŋm�F���K�v�B
濵���@�͂܁@�����B
>>786
�Ȃ�ŏ���ɊȒP�Ȗ��ɉ��肵�ē������́H
>>791
�m����5���ƌ덷��5���͈Ӗ����قȂ�
�댯����5�������e����l�͂��邪�ߎ��̌덷��5�������e����l�͒�����
���Ȃ��Ƃ�Fisher����҂����e����ƍl���鍪���͖��� >>796
�c�O�Ȃ���A�r�ɂ��̂ӂ��̈Ⴂ�𗝉��ł���m�\�͂Ȃ� >>796
���f�̌��댯���T%��e�F���Ă���̂�����덷�͈͂Ɨe�F����ƍl����͕̂��ʂ���ˁH >>799
���ʂł͂Ȃ���
�Ⴆ�Ί댯��5%�œ��v�I������s���҂����l�v�Z��p�l�����߂��Ƃ���
���̂Ƃ��ߎ��̌덷��5%������Ύg�����ɂȂ�Ȃ�
�댯����5%�����e���邱�ƂƋߎ��̌덷��5%�����e���邱�Ƃ͑S���قȂ�
5%�Ō��肷�邽�߂̐��\������덷��5�������Ă������Ȃ�ĂȂ�킯���Ȃ� >>800
���l�̕��z���l����̂��\�B
�M����Ԃ�bootstrap�ŏo���邵�B >>800
���l�Ō��肻�̂��̂��ӎU�L������
5%�ʂ͋��e�͈̔͂��ˁB >>796
�R�[�V�[���z�ł��Ƃ����ƃG���[��Ԃ��Ă����B
> pdf=\(x) (1/pi)*1/(1+x^2)
> mu=integrate(\(x) x*pdf(x),-Inf,Inf) |> print()
0 with absolute error < 0
> mu=mu$value
> integrate(\(x)(x-mu)^2*pdf(x),-Inf,Inf)
Error in integrate(function(x) (x - mu)^2 * pdf(x), -Inf, Inf) :
the integral is probably divergent >>802
���O�����e���镪�ɂ͏��肾����>>773�ƌ����Ă����
���������O�̒�����Fisher�搶�������ނ� >>804
5%����ɂ����̂�Fisher����Ȃ��́H >>806
�댯����5%���̗p�����̂̓t�B�b�V���[
�������ߎ������Ƃ��̌덷��5%�͋��e�����ȂǂƂ��������͎咣���Ă��Ȃ� ���́u�덷5%�̉������������́H�v�ƕ����Ă���Ɨ\�z�B
�ȉ����[�v�B
�t�B�b�V���[�͊댯��5%���̗p�������A������Ƃ�����
�Ⴆ�Ώc����10�̐����`�̖ʐς𐔒l�v�Z����95����105�̊Ԃ̐��ɂȂ����̂�
�u�ߎ����Ă�̂Ŗ��Ȃ��v�Ȃ�Č����킯�Ȃ����
�댯����5%�ƌ덷��5%�͑S���W�Ȃ���
�A�r�Ɂu�P�ɋ߂����v�ȏ�̈Ӗ������͗����ł���n�Y�Ȃ�
�������|���Z�̎��ɍŌ�܂ŕ�������̂��f��������
����ȃJ���W 12=2�~2�~3
��������ł��̂���������
����ȃJ���W x^2+2x+1=(x+1)^2
�������̌v�Z�͕��G������A���������̕��@�͕������̃p�^�[�������Ŋo����̂���ʓI�B
>>810
����ς�t�B�b�V���[����˂�����B >�u�ߎ����Ă�̂Ŗ��Ȃ��v�Ȃ�Č����킯�Ȃ����
���̍����́H
�T���̃��X�N�͋��e���Ă��邩��댯���T���Ȃ�B
5%�Ƃ��������o�Ă��Ă�ȏ�̗����͂ł��Ȃ��`���p���W�[
>>815
���w���ł��ł���ȒP�Ȗ���5%���̌덷�ŋߎ����o���Ė�������o�J�͂��Ȃ����� �X���Ⴂ�𑱂���L�`�ɂ�
(1.714564-12/7)/(12/7)=0.0001623333333
��5%�Ɍ�����
5�����������炢�������B
�t�B�b�V���[��5%�̔��f�̌��͋��e���Ă�����B
���f�̌�肪5%�ł��Ȃ�
�������������킩���ĂȂ��\����
���͂����Ƃ킩���Ă�̂��킩���Ă�Ƃ����T���̂�������x���̔\����
���ʃ��ɑ��C��ABC�̊e���_A,B,C��ʂ蕽�ʃ��ɐ����Ȓ����ƃ��Ƃ̌�_�����ꂼ��AA�f, B', C' �Ƃ���B
���̂悤�ɂ��ē���ꂽ��A'B'C'����ABC�̕��ʃ��ւ̐��ˉe�ƌ����B
�C�ӂ́�ABC�ɑ��A��A'B'C'�����O�p�`�ɂȂ�悤�ȕ��ʃ������݂��邱�Ƃ������B
>>820
�댯��5%�͂��̊m���ȉ��Ŕ��f����邪����͋��e������Ă��ƁB�L�Ӑ������댯���Ƃ��Ă�鏊�ȁB >>823
�Ԉ���Ă邱�Ƃ�������d�˂��Ƃ���Ő����ɂȂǂȂ�Ȃ����������ł��Ȃ��i���̃`���p���W�[ ����ƍ����̎O�p�`�͑�����3:4
���̒��p�O�p�`�̂Q�ӂ̔��x:y�Ƃ���(x<y)3y+4x = 4y
�� x:y = 1:4
�����x:y:��(x²+y²) = 1:4:��17
����č�����̎O�p�`�̖ʐς�1/2�~1/��17�~3�~4/��17�~3=18/17
�����:�����`=18:256������
�����`=256/18�~18/17 = 256/17
�����悭�ǂ݂܂��傤�B
�����Ă邯�ǂˁB
�O>>805
>>825
���p�O�p�`�̖ʐς�6
�����`�̖ʐς�6�~2=12
����ӂ̒�����2��3 >>825
(x+y)^2+y^2=4^2
x^2+z^2=3^2
(x+y-z)^2+(x+y)^2=5^2
�̐����������߂��
x=12/��17
y=4/��17
z=3/��17
x+y=16/��17 1,2,3,4,5�̐����������ꂽ�J�[�h��1��������B
����5���̃J�[�h����3����I��ŕ��ׂ�3�����̐������B
���̐�����4�̔{���ɂȂ�m����P�A5�̔{���ɂȂ�m����Q�Ƃ���Ƃ�
P:Q�����߂�B
�Ƃ������͓�����5�F4�ł��傤���B
>>830
�A�r�Ƃ͐E��̌����Ȃ���Ï]���ҁ��A�r���܂���W�̈����e��ł���B�C�Ǒ}�ǂ��ł��Ȃ������i�҂Ȃ̂�m3�ɓ��e�ł����B
�A�i�t�B���L�V�[�ł�Kounis�nj�Q�̌��͕��ɂȂ����B P(5�̔{��)
=P(1�̈ʂ�5��I��)
=1/5
P(4�̔{��)
=P(1�̈ʂ�2,10�̈ʂ�1,3,5) + P(1�̈ʂ�2,10�̈ʂ�4)
= 1/5�~3/4 + 1/5�~1/4
= 1/5
>>831
> a[a%%4==0]
[1] 124 132 152 312 324 352 412 432 452 512 524 532
> a[a%%5==0]
[1] 125 135 145 215 235 245 315 325 345 415 425 435
�ǂ����12�Ȃ̂�1:1 1,2,3,4,5,6,7,8,9�̐����������ꂽ�J�[�h��1��������B
����9���̃J�[�h����3����I��ŕ��ׂ�3�����̐������B
���̐�����4�̔{���ɂȂ�m����P�A5�̔{���ɂȂ�m����Q�Ƃ���Ƃ�
P:Q�����߂�B
�w�܂萔����
���@�Q�F�P
1,2,3,4,5,6,7,8,9�̐����������ꂽ�J�[�h��1��������B
����9���̃J�[�h���炎����I��ŕ��ׂĂ������̐������B ����1���̐��̐����B
���̐�����4�̔{���ɂȂ�m����P���A5�̔{���ɂȂ�m����Q���Ƃ���Ƃ�
P��:Q�������߂�B
��. Pn:Qn=2:1
>>837
���������o�J�Ȗ���p�����������Ȃ��o����Ƃ���ɒꔲ���̃A�z�������� �q�ǂ��̃f�b�T�����ē����ł���
>>834
0����1�̊Ԃ̒l������l���z�ɏ]���m���ϐ�X�ɑ��邻�̋t���̊��Ғl�́H �O>>828�����B�}�����������C������B3���Z���ٗl��4�������B5�͂܂��܂������ǂ��傢���߁B���p�O�p�`�̉s�p�������`�̉E�����ɂȂ��Ȃ�������̂�B����H�@�t��4���傫����4�̕ӂ������`�̉��ӂɒ����Ă܂���ˁH�@�Ă��Ƃ͂��ꂩ�A2��3��4��2��6�ŁA���Ȃ�����邢�����ł��Ȃ��B
>>805
���p�O�p�`�̖ʐς�6������A
3�~4�̒����`�̖ʐς�12�ŁA
��������鐳���`�̖ʐς�24
����ӂ̒����́�24=2��6=4.89897948557�c�c >>754
��ӂ�7�̐����`ABCD���l����
BC���BE=2�ƂȂ�_D����聢ABE���l���AA�𒆐S��90�x��]����ADF�Ɉڂ�
��EAF=��BAD=���p�AAE=AF������A��AEF�͒��p�ӎO�p�`�Ł�AEF=45�x���
�A+�C=��FEC+��AEB=180�x-��AEF=135�x >>832
�A�r�W�W�C����w
�A���J�����ĂȂ��̂Ɉ�̂ǂ����Ă���Ȃɔ������Ă�̂��ȁH �܂������c�O�Ȑl���ςȂ��ƌ���������
�O>>842�A���J�[�����B
>>825
���p�O�p�`�̖ʐς�6������A
3�~4�̒����`�̖ʐς�12�ŁA
��������鐳���`�̖ʐς�24
����ӂ̒����́�24=2��6=4.89897948557�c�c
�A���A���p�O�p�`�̉s�p�������`�̉E���̒��_�ɒ����Ă��Ȃ����Ƃ��C�ɂȂ�B �O>>846
>>825
�����`�̈�ӂ̒�����x�Ƃ����ƁA
�Εӂ�3�̒��p�O�p�`�ƎΕӂ�4�̒��p�O�p�`�͑����ő�����3:4������A
�Εӂ�3�̒��p�O�p�`�ɂ����钼�p�����ޒ��ӂ̒�����3x/4
�Εӂ�4�̒��p�O�p�`�ɂ����钼�p�����ޒZ�ӂ̒�����x/4
�Εӂ�4�̒��p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
(x/4)^2+x^2=4^2
17x^2/16=16
x��17=16
x=16��17/17
=3.88057000058�c�c ���̌v�Z���č����Ă�H

1~10��10�̎��R����������ɕ��ׂ�Ƃ�
�אڂ���2�����K��5�ȏ�̍��ɂȂ�悤�ȕ��ו���2�ʂ�ł��傤���B
5,10,4,9,3,8,2,7,1,6.
6,1,7,2,8,3,9,4,10,5.
�����2�ʂ�ȊO�ɂȂ����Ƃ������̂͊ȒP�Ɏ����܂����H
5�͒[����
5�ׂ̗�10
4��9��10�̊�
3��8��9�̊�
2��7��8�̊�
1��6��7�̊�
�ȏ�
10!=3628800�ʂ肩������ɍ��v���鏇����v���O�����ɒT������
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 5 10 4 9 3 8 2 7 1 6
[2,] 6 1 7 2 8 3 9 4 10 5
2�ʂ�
���܂�
1~10��10�̎��R����������ɕ��ׂ�Ƃ�
�אڂ���2�����K��4�ȏ�̍��ɂȂ�悤�ȕ��ו���1496�ʂ�B
[1,] 1 5 9 2 6 10 4 8 3 7
[2,] 1 5 9 2 7 3 8 4 10 6
[3,] 1 5 9 3 7 2 6 10 4 8
...
[1494,] 10 6 2 8 4 9 5 1 7 3
[1495,] 10 6 2 9 4 8 3 7 1 5
[1496,] 10 6 2 9 5 1 7 3 8 4
>>855
854�̂悤�ȓ����͖��Ӗ��H 1,2,3...,,10��10�̎��R�������ɕ��ׂ�Ƃ�
�אڂ���2�����K��2�ȉ��̍��ɂȂ�悤�ȕ��ו���208�ʂ�B
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 2 3 4 5 6 7 8 9 10
[2,] 1 2 3 4 5 6 7 8 10 9
[3,] 1 2 3 4 5 6 7 9 8 10
[4,] 1 2 3 4 5 6 7 9 10 8
[5,] 1 2 3 4 5 6 8 7 9 10
[6,] 1 2 3 4 5 6 8 10 9 7
....
....
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[203,] 10 9 8 7 6 5 3 1 2 4
[204,] 10 9 8 7 6 5 3 4 2 1
[205,] 10 9 8 7 6 5 4 2 1 3
[206,] 10 9 8 7 6 5 4 2 3 1
[207,] 10 9 8 7 6 5 4 3 1 2
[208,] 10 9 8 7 6 5 4 3 2 1
>>856
���l�߂Ő������o���铪�]�͑��h����B ���p���
2,3,4,5,6,7,8,9��8�̎��R�������ɕ��ׂ�Ƃ�
�אڂ���2�����݂��ɑf�ɂȂ�悤�ȕ��ו��͉��ʂ肠�邩�H
����𗝋l�߂ʼn����铪�]�͏^�ł���B
2,3,4,5,6,7,8,9��8�̎��R����אڂ���2�����݂��ɑf�ɂȂ�悤�ɕ��ׂ�8���̐��������B
��@234569789�@25678943�Ȃ�
����8���̐��������������ɕ��ׂ�Ƃ�333�Ԗڂɂ��鐔�������߂�B
>>860
��t����f���ŃA�i�t�B���L�V�[��Kounis�nj�Q�̋c�_�����Ă��邯��
�A�r���܂���W����A�N�Z�X�͂ł���B >>863
�]����҂����Ҕœ˂����܂ꂽ���e�Ƀ_���}�������ł��Ȃ�����w
�A�r�W�W�C�͐��w�ł��S������ɂ���ĂȂ����Ƃ��悭�������� 5,7��A�@2,4,8��B�@3,9��C�Ƃ���
B��B��B�����@�@B����BCB���A�@BCB����B���B�@��B��B��B���C�Ƃ���
�ꍇ1�@6�����Ԃɂ���Ƃ�
���̏ꍇ�A6�̗��ׂ�A������A6A�Ƃ�����ɂȂ�A���̗��D�Ƃ���
�@�́���D��C���u���d����3�ʂ肾����ꍇ�̐���3*3!*2!*2!=72
�A�́���D��C��u���d����2�ʂ�ŏꍇ�̐���48
�B�͇A�Ɠ��l������ꍇ�̐���48
�C�͇@�Ɠ���������ꍇ�̐���72
�ꍇ2�@6�����[�ɂ���Ƃ�
���̏ꍇ�A��Ԗڂ�A�����ĎO�Ԗڈȍ~�̕��т��@�`�C�ɂȂ�
�@�́���A��C���u���d���͏ꍇ1�̂Ƃ��̇@�Ɠ���
�A�́���A��C��u���d���͏ꍇ1�̂Ƃ��̇A�Ɠ���
�B���ꍇ1�̂Ƃ��̇B�Ɠ����ŇC�����l
�@
�ꍇ3�@6���E�[�ɂ���Ƃ�
���̏ꍇ��7�Ԗڂ�A��������8�Ԗڂ�6������A1~6�Ԗڂ��@~�C�ŕ\��
���̏ꍇ�ɂ�����@�`�C�̏ꍇ�̐��͖��炩�ɏꍇ2�̂Ƃ��̂���Ɠ��l
�擪��B�ł���ꍇ�̐��́@�ꍇ1�܂��͏ꍇ3�ɂ�����@�A�B�̂��ꂾ����(72+48+48)*2=336
�ꍇ1�Ő擪��C�ł���ꍇ�̐��́@�C��CB��B��B�́���D��C��u���d����2��3!*2!*2!���|����48
�ꍇ3�Ő擪��C�ł���ꍇ�̐��́@�C��CB��B��B�́���A��C��u���d����2��3!*2!*2!���|����48
���킹�āA�擪��C�ł���ꍇ�̐��́@96
�擪��4�ȉ��ł���ꍇ�̐��́@112+96+112=320
�䂦�ɐ擪��5�ł����̒��ł�13�Ԗڂ�����悢
52����n�܂��́@52CBCB76�@��2!*2!��4�ʂ�
53����n�܂��́@53BCBC76�@��4�ʂ�
54����n�܂������l��4�ʂ肾����13�Ԗڂ�56����n�܂�ŏ��̂���
�ꍇ1�̇C�ɂ�����DBCBCB�Ł@56723498
�擪��5�͏ꍇ1�ɂ�����C��567BCBCB�Əꍇ3�ɂ�����C��5BCBCB76��
3!2!*2��24�ʂ�@�擪��7�����l�@�擪��6�͏ꍇ2������240�ʂ�
�擪��2�ł���ꍇ�̐����珇�ɕ��ׂ�Ɓ@112,96,112,24,240,24,112,96�@�v816
�ԈႦ���@
�擪��2�ł���ꍇ�̐����珇�ɕ��ׂ�Ɓ@
112,48,112,24,240,24,112,48�@�v720������
�擪��5�ȉ��ł���ꍇ�̐���296������擪��6�ł�����т�37�Ԗڂ�����悢
652�ɑ������т́@��B��B���@����B��B�@�́���7��C�������d��������
�O��3�ʂ���2�ʂ�ŏꍇ�̐���5*2!*2!=20
653�ɑ������т́@B��B��B�@�́���7��9������d���ŏꍇ�̐���2!*3!=12
�擪��654�ɑ������т����������ɕ��ׂ�Ɓ@
32789�@32798�@32978�@32987�@37298�@������333�Ԗڂ�65437298
�v���O�����ɗ������
> sort(z)
[1] 23456789 23456798 23458976 23459876 23476589 23476598 23478956 23479856
[9] 23495678 23495876 23497658 23497856 23498567 23498576 23498756 23498765
...
[305] 65238947 65238974 65273498 65273894 65274389 65274983 65278349 65278943
[313] 65279438 65279834 65294378 65294387 65294738 65294783 65297438 65297834
[321] 65298347 65298374 65298734 65298743 65327498 65327894 65329478 65329874
[329] 65347298 65347892 65349278 65349872 65387294 65387492 65389274 65389472
[337] 65432789 65432798 65432978 65432987 65437298 65437892 65438729 65438792
....
[705] 98325476 98325674 98327456 98327654 98345276 98345672 98347256 98347652
[713] 98523476 98543276 98567234 98567432 98723456 98743256 98765234 98765432
�z�肵��������
> z[333]
[1] 65387294
65437298��341�Ԗ�
> which(z==65437298)
[1] 341
���Đ�����̂łȂ����l�߂œ����o���铪�]�Ɋ����B
�ǂ����������Ȃ̂��͂悭�킩��B
���̃v���O�������Ԉ���Ă��邩�������̂ő�����ł̌��؊�]�B
>>13
���܂�R�ł̓��v��͂ł�FDA�͔F����قǕ��y���Ă���B
�������̐V�^�R���i�W�Ƀy�[�p�[��R���g���Ă���̂��������B
�������Z��̃p�����[�^����j��R�̃p�b�P�[�W��fitdistrplus���g���Ă����Ȃ��B
8�����������R-user
�R�[�h�����J����Ă����̂ʼn���R�ő��点�Ă݂��B
R�̂��܂��@�\�ł��������̂�����B
2,3,4,5,6,7,8,9��8�̎��R����אڂ���2�����݂��ɑf�ɂȂ�悤�ɕ��ׂ�8���̐��������B
��@234569789�@25678943�Ȃ�
����8���̐��������������ɕ��ׂ�Ƃ�333�Ԗڂɂ��鐔�������߂�B
�A�r���܂���W���ᗠ���e�^�҂̃V���c��ɂ͖����B >>867
��652�ɑ������т́@��B��B���@����B��B�@�́���7��C�������d��������
���ꂪ�ԈႢ
652�ɑ������т́@��B��B���@����B��B�@��B����B�@��3�p�^�[��������
���́���7��C�������d���͂��ꂼ��3,2,2�@�ꍇ�̐���(3+2+2)*2!*2!=28
�䂦��653����n�܂�9�Ԗڂ̂��̂������ɂȂ�
653B��B��B�Ł���7��9�����č������3!2!=12�ʂ肾����
�傫�����ɂȂ�ׂ��@89472�@89274�@87492�@87294�@
��4�Ԗڂ�����������9�Ԗڂ�����@65387294 >>871
m3�ł��o�J�ɂ���Ă�A�r�W�W�C
�����ł��o�J�ɂ��ꂽ�����H >>871
���C�s���ĂȂ��̂ɂȂ�Ő���̎��i�Ȃ��Ƃł��Ȃ��d�����ł����H >>874
�]����Â̓u���b�N�W���b�N�Ȃ�ł�w ��t����̌f���ɂ͔A�r���܂���W�̓A�N�Z�X�ł��Ȃ�����Ȃ��B
�f���̓��e�͌��J���܂���A�ɓ��ӂ��ăA�N�Z�X���邱�ƂɂȂ��Ă��邪�A�R�s�y��\���Ă���ᔽ�҂�����B
���������s�����Ȃ�Ƃ��v��Ȃ��̂͗������w�����V���c��Ȃ̂��낤�Ɛ������Ă���B
>>874
����Ɛ��_�Ȃ̑[�u���@���炢���ȁB���i���Ȃ��Ƃł��Ȃ��̂́B
�����t�Ƌ����Ȃ��Ă�����������̂Ɠ����B
�ӂ��������Ȃ炻��Ȃ�̎��i���K�v�����ǂˁB
����̎��i�Ȃ��Ƃł��Ȃ��d���@���ĉ�����H
���R�̈�t����f���͔A�r���܂���W���A���V�ɂ��Ȃ��̂ŋƊE�l�^�̋c�_���ł���B >>877
�C���A�a�@���g�킹�Ă������H
���������ق��Ă��炦����H >>872
�ǂ����A���l�߂̌��_�ƃv���O�����ł̃J�E���g�����v�����悤�Ȃ̂�
�������v���O�����ł������悤���B >>879
���O��Ƃ��̕a�@�ł͏�����O�Ȋw��̔F���ł��Ȃ��l�Ԃɓ������g�킹�Ă����H >>880
m3�ň������ꂽ�������o�C�g��ł�������Ζ��𑝂₵�Ă���ƑŐf���ꂽ�B m3�̈�t����f���ɂ͐E��̌����Ȃ���Ï]���ҁ��A�r���܂���W�����炵�ɗ��Ȃ�����ƊE�l�^�ŋc�_�ł���(�E�́E)��!!
>>882
���̕a�@�ł͂ǂ������������œ����Ă��H
���������Ί�O�Ȉ�̌������͖����Ȃ���ȁH
�w��F��ザ��Ȃ���ȁH
���C�s���ĂȂ����� ���߂�A���̖��̓������ł����Ȃ�̂��킩��Ȃ��̂ŋ����Ă�����

�}�̔��a�G�̎��̒��������߂�Ɠ���
16�~2�~90/360��8�ɂȂ�Ǝv���Ă���
������8��+16cm�ɂȂ�Ə����Ă�������
����16�Z���`���ĉ��Ȃ́H������+16���t�����R���{�C�ł킩��Ȃ��̂ŋ����Ă����� >>883
m3�ł����X�J���H����Ă܂������ǁHw >>885
����ǂ݊ԈႦ�Ă�H
�G�͔��a����Ȃ��Ĕ��~�̌`�������}�`�̖��O�ł��傤
���a��16cm�Ȃ���~����16��cm
���~������ʂ̒����͔�����8��cm
����ɒ���������16cm��������8��+16(cm) 3x3�̏��ڂƁA���ڂ̒��̕����ɂ��Ă̖��B
�����̈ړ��������ȉ��̂悤�ɒ�`����B
�y��`�z
�ړ��O�̍��W��(a,b)�A�ړ���̍��W��(c,d)�Ƃ���Ƃ��A
�ړ������́A|c-a|+|d-b|�Ƃ���B
���������ƁA�}�ɂ����镶��A,B,C�̈ړ������̑��a�� 5 �ƂȂ�B
A�̈ړ������F|3-1|+|2-1|=3
B�̈ړ������F|2-2|+|1-1|=0
C�̈ړ������F|1-3|+|1-1|=2
�}:https://imgur.com/StWK5NB
3x3�̏��ڂ�A�`I��9���������ׂ��Ă��āA�����̕��������ׂĈړ�����Ƃ��A
�ړ������̑��a�̍ő�l�����߂�B >>887
���[�����������ȂA�����悭�킩��܂�������肪�Ƃ��������܂���
�߂���߂���v�l�̃h�c�{�n�}���Ă܂��� �p��H�̎���ł�
1, 2, 4, 8, 16...��\�����邽�߂Ƀf�[�^�ߖ�̂���
�t���̕��ꂪ2�̉��悩�ŕ\�����悤�Ǝv������ł���
�����ł�����Ə��Ԃɗp����m�F���čs����
1/1, 1/2, 1/4, 1/8, 1/16�@���t��
0, 1, 2, 3, 4�@���t���̕��ꂪ2�̉��悩�i���H�H�j
1, 2, 4, 8, 16�ɑ���0, 1, 2, 3, 4�͂ǂ��������ƕ\�������ł��傤���H
f(x) = 1/log2�݂����Ȃ��Ƃł��傤���H
�킩��ɂ����ăA�z�Ȏ���ł��݂܂���
���݂܂���C�������Ă����̂Ŏ�艺���܂�
�P��log2�ł���
�������X���Ⴂ�Ŗ{���ɐ\����L��܂���ł���
>>886
��t����f��������A�N�Z�X�ł��Ȃ������ɁB
�|�C���g�����܂��Ă����̂ŃA�}�]���M�t�g����5000�~���Ɍ��������B >>884
���͑��Ƒ�w�𖼏�邾���ŏ\���Ȃ̂�B >>893
�u�I���́~�~��w���̈�t�����猤�C�͉���ĂȂ����Ǒ��v�A���������p�������Ǘ�����������Ȃ����ǑS���ł���v
�ł����H
�A�z�`wwwwwwwwww >>892
m3�Ȃ�A���^�܂߈�҂���Ȃ��Ă��A�N�Z�X�ł��邾���Hw
����ɂ����ł��t���{�b�R�����w
�]���w���Ȃ��w��������Ă邼w >>895
�����ɏ�������m3�̈�t����f���ɏ�������
�����Ȃ����炱���ŃA���V���������Ȃ��́H
�E��������Ȃ���Ï]���ҁ��A�r���܂���W���Ď������Ȃ̂��H >>896
m3�ł��܂�ő���ɂ���Ȃ�����킴�킴�����Ŕ������Ă�Hw ������ƕ����������Ǥ���p�ӎO�p�`���������Ƃ���
��ӂ�10cm���Ƃ�����c��̈�ӂ�10cm�̓�悪�����ɂȂ�킯�H

>>898
�c��̈�ӂ͕K����2���|�����l�ɂȂ�
��ӂ�10cm�Ȃ�c��̈�ӂ�10��2cm >>898
�ǂ�ȎO�p�`�̂ǂ̈�ӂł����̓�ӂ𑫂���������蒷���Ȃ�Ȃ�
�Εӂ̒�����c�ŏc����a,b�ł��钼�p�O�p�`���l����
�����4�R�s�[����c�Ő����`�����悤�ɕ��ׂ�ƈ�ӂ�a+b�̐����`���ł���
���̖ʐς�(a+b)^2�����@4�̎O�p�`ab/2*4�ƈ�̐����`c^2�@����Ȃ�̂�
2ab+c^2�Ƃ�������̂Ł@c^2=a^2+b^2
a=b=10�@�̂Ƃ��@c^2=2*10^2�@������@c=10��2 ����e�X�g������A�O�p�`�̑����̏ؖ����Łu3�g�̕ӂ̔䂪�������v�Ə�������s�����ɂȂ�A�u���ׂē������v�������琳���������͕̂�����܂����B
�s�����Ƃ������͏�̕��ł͂��ׂē������Ɠ��`�ɂ͂Ȃ�Ȃ��Ƃ������Ƃ��Ǝv���܂������̂ł��傤���B
>>905
�S�ē��������Ă͍̂�����������i���������͑��ɂ����邯�ǁj
��蕶���ꎚ���ς����ɏ������ނ��\�Ȃ�摜�ŏグ�Ă݂� 3�g�̕ӂ̔䂪�������@�̈Ӗ���
3�g�̕ӂ̔䂪�i�S���j�������@�ȊO�Ɏ��Ȃ��Ǝv����
�搶�Ɍ���Ă��Ȃ��H
�u���ׂē������v�łȂ���
�����ȕ��͂Ƃ��Ă͕s�K���ł����
���f���ꂽ�̂ł͂Ȃ����B
��蕶�����Ȃ��Ƃ͂����肵�����Ƃ͌����Ȃ����B
�u�R�g�̕ӂ̔䂪�������v�̓_���Łu�R�g�̕ӂ̔䂪���ׂē������v����Ȃ���_�����ĈӖ��Ȃ̂��ȁH
���ȏ��ʂ�̕\��������������Ă������t�͈�萔����݂�����
�Ƃ͌�����{�I�ɂ͎̂��߂ɂ���Ă邾�낤���炻��Ȃ炻�̂ق������S
�̓_���ƃP���J���Ă����傤���Ȃ�
�����ւ̏������݂��������[���ŏȗ����Ă��܂�������A������ƋC��t�������������Ƃ͎v��
>>905
A�FB�FC�͑��������i2A�F2B�F2C�ł͍����ɂ͂Ȃ��ł���
A��B��C���������� �x���Ȃ�܂����A905�ł��B
�摜�\��̏��߂ĂȂ̂ł����Əo���Ă邩������܂��A���̖��̃G�̗��̓������u3�g�̕ӂ̔䂪�������v�Ə����ĕs�����ł����B
�ł́u3�g�̕ӂ̔䂪���ׂē������v�ƂȂ��Ă��܂��B
����ƃ��[�����ȗ����Ă��܂����Ƃ̂��ƂŐ\����܂���ł����B
https://imgur.com/6p6vBcy >>911
���傤���ˁ[��A�^���Ȃ������Ǝv���Ē��߂� >>911
�O�p�`�̑��������̕����͋��ȏ����ƂɁA�N�ゲ�Ƃɔ����ɕς���Ă��肻�̒��x�̈Ⴂ���o�c�ɂ���̂͌l�I�ɂ͈Ⴄ�Ǝv��
�����e�X�g�O�ɂ�����L�`���Ɩ��L����悤�Ɏw������ꍇ�͂���ɏ]���K�v�����邾�낤
���j�̃e�X�g�Ől�����������ŏ����Ȃ���_���Ƃ����e����Ƃ��������Ŏw������s�ׂ͎��ۂɂ悭����b�������e�͈͓��� �����̏ꍇ�͏��w���ɂ͏d�v������l�����������Ɋ����v������Ӗ��͕����邯�ǂ�
�O�p�`�̑����������q�ׂ�Ƃ��̕����ɓ�̒��������Ӗ��͕�������
�u3�g�̕ӂ̔䂪�������v
���̕��͂�
�u3�g�̕ӂ̔�̂����̂����g�̔䂪�������v
�Ɖ��߂ł���Ƃ͎v���Ȃ�����
�ua,b,c���������v�Ƃ����ua=b=c�����藧�v�ȊO�̓ǂݕ��Ȃ��Ǝv��
>>916
���������̃p�^�[���ƈ��Ղɓ����ƍl���Ďv�l��~���鐶�k�̗\�h������ >>918
�ǂ����������ŗ\�h�ɂȂ�́H �Ȃ����
���̉��߂Ȃ�
�u3�ӂ̒������������v
��
�u3�ӂ̒����̂����ꂩ1�g���������v
�̈Ӗ��Ɏ���邩��~��
�u3�ӂ̒����̑S�Ă��������v
�Ə����Ȃ��ƃ_���Ƃ��������ɂ����Ȃ�Ȃ�
�܂�g��h�Ɓg�����h�̒P�ꂪ����Ă������ɂ����Ȃ�Ȃ�
�摜�̐����`�̒��ɂ��鐳���`B�̖ʐς��Ăǂ��v�Z����́H�����������Ă������i�G�͈Ӗ��Ȃ��j

�Q�̎O�p�`�̕ӂ̒����� a, b, c �� x, y, z ���Ƃ��Ă���B
�O�p�`�̍��������́u�R�ӂ̒��������ꂼ�ꓙ�����v����
a=x , b=y , c=z �݂����Ȏ��ɂȂ�B
���������Łu���ׂāv�������ꍇ�A������������
a:x = b:y = c:z �݂����Ȏ������v�����Ȃ����k���������Ƃ�����B
����őS�Ă�t����ƁA���������ƈႢ
a:b:c = x:y:z �Ƃ����ꍇ�����邩��C�����悤�Ƃ������ӊ��N�ɂȂ�B
��̎��Ɖ��̎��͓���ւ������A���̏ꍇ���߂ɖ��ł��ĕ��������ƂĂ��ȒP�ɂȂ鎞������B
>>921
B�̖ʐς͐����`�̖ʐς̔����B�c���̒��S����\���̕⏕���������āA�O�p�`���ړ�������킩��B
���������� 20�~20��2=200 >>922
a:x = b:y = c:z
�Ɖ��߂��ĂȂɂ��������H >>922
���������̂͗ޑ���R���ΐg�ɂ������Ȃ���ΐg�ɂ��Ȃ�
���������̕����̈ËL�̎d���̖��ł͂Ȃ��C�����܂� ���O�O���Ă݂�
�O�p�`�̑���������3�ӂ̒����ŗ^������@�Ƃ��Ă͂Ƃ��čl������̂�
a : b : c = p : q : r
��
a : p = b : q = c : r
���l�����邯�ǃO�O�����͈͓��ł͌�҂łƂ������������
���苳�ȏ��łǂ��Ȃ��Ă�̂��m��ǃO�O�����������炷��ƌ�҂Ȃ���
���Ƃ����琶�k�ɂ́u��҂̈Ӗ��ɂƂ�ꂩ�˂Ȃ�����_���v�Ƃ͌�����ȁA�ނ��낱�����̈Ӗ��ɂƂ��Ăق������炢�Ȃ�₩��
�������u�����܂ŋ��ȏ��ł̒�`�͌�҂őO�҂ł͂Ȃ��A����đO�҂̈Ӗ��Ɏ���Ȃ��悤�Ɂg�S�Ắh�����Ƃ��ׂ��A���ꂪ����Ό�҂̈Ӗ��ɂ����Ƃ�Ȃ��v�Ȃ炻��͂��邩�������A���邩�����������Ƃǂ��Ȃ���Ċ���
>>915
>�O�p�`�̑��������̕����͋��ȏ����ƂɁA�N�ゲ�Ƃɔ����ɕς���Ă���
����Ȃ��ƂȂ��B�ǂ̎���̂ǂ̋��ȏ��ł������B���Ȃ��Ƃ�����́u���ׂāv�͕K���t���Ă邵�A�K���t����ƏK���͂��B
�ؖ��͌����������߂���B�u3�g�̔䂪�������v�ƌ���ꂽ��펯�I�ɂ͂��ׂē������Ɖ��߂��邾�낤���A���߂����߂鎞�_�ŏؖ��Ƃ��Ă͕s�\���Ƃ������Ƃ��B >>923
��������o����Γ����̎l�p�ʐς��O���l�p�̓̈�ɂȂ闝�R�������Ă����� >>921
�����`B�̂P�ӂ̒��������Ƃ���Ɩʐς�x^2
���͒��p�ӎO�p�`�̎Εӂ̒����ł����邩��O�����̒藝����x^2=10^2+10^2=200 >>921
�Ђ��`�̖ʐς͑Ίp���~�Ίp����2������200 >>928
���̃X�N�[��TV�Ƃ�炪�Ԉ���Ă邾���B��������Ȃ�Ă���Ȃ���B >>929
�����̎l�p�ɑΊp���̕⏕��������ƁB 905�ł��B�v���̊O�����̃��X���t���Ă��ċ����܂����B
���̃T�C�g�ɒ��ׂɍs���Ē��������܂ŋ��ċ��k�ł��B
���X�����ꂽ�F�l���肪�Ƃ��������܂���
>>927
>�ǂ̎���̂ǂ̋��ȏ��ł������B���Ȃ��Ƃ�����́u���ׂāv�͕K���t���Ă邵�A�K���t����ƏK���͂��B
����͈Ⴄ�B�u�Q�g�̕ӂ̔�Ƃ��̊Ԃ̊p�v�Ȃ����ɔN�㖈�ɕ\��������Ă���B
���ȏ��ł͂Ȃ����A���n���w�}�𒆊w���̐��w���� 8�@�}�`�̑����x��菑�X�A���a40�ł�
https://dl.ndl.go.jp/info:ndljp/pid/1655793
�u�Ή�����O�g�̕ӂ̔䂪�������v�ƂȂ��Ă���A�u���ׂāv�͂Ȃ��B
�֓����w���w���̐��w�����@�킩�鍇���Ƒ����x��菑�X�A1959�ł�
https://dl.ndl.go.jp/info:ndljp/pid/2440110
�藝39�ł́u�O�g�̕ӂ̔䂪���ׂđ���������̎O�p�`�͂������ɑ����ł���v�ƂȂ��Ă��邪�A���y�[�W�̂܂Ƃ߂ł�
�O�p�`�̑��������Ƃ��āu�O�g�̕ӂ̔䂪�������v�ƂȂ��Ă���u���ׂāv���������Ă���B
���Ȃ݂ɁA����}���ق̃����N�͓o�^�K�v >>936
����́u���ȏ��v�ƌ����Ă��B
���͂͐������ǂ݂܂��傤�B���������Ƃ�����w >>924
�����ȎO�p�`�̂Q�̕ӂ����ꂼ��
2x-4 �� x+1 �C 42 �� 30 �ƂȂ��Ă���ꍇ
2x-4 : 42 = x+1 : 30 �Ɣ�̎������Ă���
2x-4 : x+1 = 42 : 30 �Ɨ��������āA�E�ӂ� 7:5 �Ɩ����������|�I�ɊȒP�Ȍv�Z���ł���B
�ǂ�������������ɂȂ邪�A�ԈႢ���l����Ɖ��̎��Ōv�Z�o�����ق����]�܂����B �ł��������ɏ��a40�N�Ƃ�1959�Ƃ��̋��ȏ��܂Œm���w
���Ȃ��Ƃ������ȍ~�̋��ȏ��ňႤ�\�����������Ƃ͂Ȃ��ȁB
>>937
���ȏ��ł��Ⴄ�悗�@�ł��A�m���߂悤�ɂ������N��������ȁB
���́u���ׂāv�����L����Ă���̂͂܂��������낤�B
�̂̎Q�l���ł͖��L����Ă��Ȃ����̂����邩�炻����Q�l�ɂ��ĉ��������k�����邾�낤���Ȃ��B
�܂������Ŏw���������@�ŏ����Ȃ��Ⴂ���Ȃ��͎̂d���Ȃ��Ƃ��Ă��B ���ȏ��̖��������Ă��Q�l�����ɂ͉���ڂ��Ȃ����獢��
>>939
���w�Z�̊����̋L�q�ȂA���ȏ��ɂ���āu����ׂ���ʁv�Ɓu����ׂ�ʁv�̋L�q������Ă��ăG���N�������邼�� >>940
���a40�N�̋��ȏ����钆�w���Ȃ�����w
�������Ɍ����ꂵ�߂���B >>943
�_��ɂȂ���Ă��Ƃ��悗
�����Ŏw�����ē������Œ肷��̂܂Ŕے�͂��Ȃ����B �̂ƍ��ňႢ������Ƃ������Ǝ��̂��{���ɂ͉��̊W���Ȃ��Ƃ����؋�����
��͎̂O�p�`�̍��������ȂO�ӑ����A��Ӛ�p�����A��p��ӑ����Ƃ�����Ă����Ƃ����b���ȁB
�������悗
����������
�O�Ӕ䑊���A��Ӕ��p�i��Ӕ��p�����j�A��p����
���ȁB�����ȏ������̍��ق��ł��邩��A����ňËL������̂����肩�H
>>946
����͍��ł��������B�����ł͋����Ȃ����A�����ł͌��\�����Ă�B��{�I�Ɍ������Z�͎��Ȃ����狳�ȏ��̕\�L�ɂ������K�v�Ȃ�����ȁB �܂��l������͈̂ꉞ�����ɂ�
a:b:c = x:y:z �� a:x = b:y = c:z
�ł͈Ӗ������Ⴄ��ƁA��҂Ȃ�u�������藧�ȈӖ��Ȃ�₩��g�S�Ắh���Ƃ��v����
��������������Ł~����搶�͂ǂ��Ȃ���Ďv��
�~����Ȃ�~����ꂽ���k���[���s���܂Ő������Ȃ���
�~�͂���A�����͂��Ȃ��ł͂Ȃ��Ȃ��Ƃ�������
>>943
�ӊO�Ɛe�Ƃ��c����̑������
�}���ِ}�����Ö{���ŌÂڂ����{��ǂނ悤�ȃK�L�͋���Ǝv���Ă����B ���ǂ̎���̂ǂ̋��ȏ��ł������B>>927
�����Ȃ��Ƃ������ȍ~�̋��ȏ��ňႤ�\�����������Ƃ͂Ȃ��ȁB>>939
�g�[���_�E�����܂��� �s�������[�������Ȃ��Ƃ��ł͂Ȃ��A��������Ȃ��}�`���܂�ł��܂��P�[�X������̂Ń_��
�݂����ȗ��R������Ȃ�m�肽���Ǝv�����̂ł����A�F�l�̃��X����������
���ׂĂ�����̂��ԈႢ�̂Ȃ��x�X�g�ȉł��邱�Ƃ͓��R�Ƃ���
���ƌ����āu3�g�̕ӂ̔䂪�������v���ԈႢ�ł��閾�m�ȍ����������ł��Ȃ��Ƃ��������ł��傤��
���ɊԈႢ���Ƃ���ƊԈႢ�{���炯�ɂȂ邩���
���݂̋��ȏ��̕����ƈႤ�Ƃ������R�ő��̖{���ԈႢ�Ă��͂������܂���
�u���ׂāv�̑���Ɂu���ꂼ��v���t���Ă�Ɩ��m�Ɂ~������
�����t���Ȃ��Ɓu���ׂāv�̈Ӗ��ɂȂ�����
>>951
�܂����l������ˁB�ԈႢ���ۂ��Ō����ΊԈႢ�ł͂Ȃ��B
�ł��e�X�g�Ō��_�����ȏ㐳�m�ɏ����ׂ����낤�B
�ԐM���œ˂�����ł���ԂɁu����͐M��������Ă邩�琳�����v�ƌ����ă��U���U�͂˂��邱�Ƃ�����܂��B �܂��ł������̒�`���u�g��k������ƃs�b�^���d�Ȃ� �v�Ȃ�u���ׂāv�͂���ȁB��`�����Ă��邱�Ƃ��������߂ɂ́B
a:b:c=x:y:z�ł͂��̂܂ܓǂނƁu�`�����v�Ƃ������Ƃ�����ȁB
�u�Ή�����ӂ̊g�嗦���ǂ��������v��\�����߂ɂ�a:x=b:y=c:z���������A����m�ɕ\������ɂ́u���ׂāv�Ɠ��ꂽ�����ǂ����Ƃ͊m���B
�u�R�g�̔䂪�������v�Ƃ����\�L���������ꍇ�A
a:b:c = x:y:z
�̗l�ȈӐ}�̌��y�Ƃ�
a:x = b:y = c:z
�̗l�ȈӐ}�̌��y�Ƃ�����B
����̏ꍇ�́A���ʓI�ɓ������e�ɂȂ�Ǝv���邪�A
0���܂ނ悤�ȏꍇ�ł́A�咣���قȂ��Ă��܂��B
�������A�u�R�g�̔䂪�S�ē������v�ƂȂ�A��҂��Ӑ}���Ă���Ǝ���B
�u�݂��ɑf�v�Ƃ������t�����邪�A�������̂�������Ȃ��B
�ua �� b ���݂��ɑf�v�Ȃ�A���͋N����Ȃ����A
�ua �� b �� c ���݂��ɑf�v�́AGCD(a,b,c)=1 ��\�����ƂɂȂ��Ă���͂��B
�������A������A���邢�́A�ǂݎ肪 GCD(a,b)=GCD(b,c)=GCD(c,a)=1�@���Ӑ}���Ďg���Ă���A
���邢�́A��ǂ��Ă��܂���������Ȃ��̂ŁA���ӂ��K�v�B
��҂��Ӑ}���Ă���ꍇ�́A�ua �� b �� c �͂ǂ̓���݂��ɑf�v�̗l�ɕ\���Ȃ��Ƃ����Ȃ����A
���̏��A�����ua �� b �� c ���݂��ɑf�v�ƕ\�����Ă��܂�����A���B
�u�Ӗ����m�肵�Ȃ��悤�ȕ\���͎g���ׂ��ł͂Ȃ��v�Ƃ������ƁB �u6��2(1+2)�v�ɒʂ��邩������Ȃ��B
�܂����w�����炢�����a,b,c>0�ɑ���
a:b:c = p:q;r �� a:p = b:q = c:r
�͎����ƌ����Ă������x���������ێȂǂ̏�ʂł͑S����莋����Ȃ�
���̓R�����g�����h�Ƃł��Ȃ����w���̊w�K�̒i�K�łǂ������������ǁA�R�����g�_���h�Ǝw������ɂ͑���̐��k��
�E a:b:c = p:q;r �� a:p = b:q = c:r�ɂ�a,b,c>0����͂Ȃ�
�E�������Ȃ���a,b,c>0�łȂ��ł͔��������A�Ȃ̂ňӖ������͈Ⴄ
�E���ȏ��̒藝��a:p = b:q = c:r�̑����Ȃ̂�a:p = b:q = c:r�̈Ӗ��ł��鎖���m��ł���\���ɂ��ׂ�
�Ƃ�������[����������łȂ��Ȃ�P�Ȃ鎩�Ȗ����ł����Ȃ�
�_�����A���R�͂킩��Ȃ��Ă������A�_�����A���R�͂ǂ������O�ɂ͕������Ȃ�_�����Ǝw������Ӗ��͂Ȃ�
�uAB:CD=BC:DB=CA:BC�@���R�g�̔䂪���������瑊���v�@�Ə����Ă���̂�����
AB:CD=BC:DB=CA:BC�@�̈Ӗ��ŎO�g�̔䂪�������ƌ����Ă�͖̂������Ǝv����
�m���ɂ��Ƃ̎���̕��͂�
�u3�g�̕ӂ̔䂪�������v
�Ȃ̂łł���Ȃ� a:b:c = p:q:r �̈Ӗ��ɂ͂Ƃ�Ȃ���
3�g�ƌ����Ă�̂�����
��������́u�����̂Ƃ��́g�S�Ắh���Ȃ��ƃ_���v�ƈӖ��������炸�Ґ����˂Ł~�����搶���n�Y���Ƃ��������悤���Ȃ��̂�����
�������m�̊���Z���炵��
��d�v�l�����B�������ĂȂ����w5�N���łׂ͉��d�����炢������Ȃ�
a:b:c = p:q:r �� a:p = b:q = c:r
�������łȂ��q���U���ɋ���
����͌o����P�Ɏw�����₷�����炾�Ǝv���Ă����ǂȁB
���̑��������⍇�������̏ꍇ�A�u���ꂼ��v�Ƃ��Ȃ��ƈӖ����ς�邩��K�v�B
����Ɓu3�g�̕ӂ̔䂪���ꂼ�ꓙ�����v�Ə����Ă��܂��q�����o���邩��u3�g�̕ӂ̔�̎�������(���ꂼ��ł͂Ȃ�)���ׂĂƕK�������Ȃ����v�Ǝw�������B�܂�A�u���ꂼ��v�Ə������Ȃ����߂ɁB
�����珑���Ȃ������猸�_�Ƃ����̂͐����i���Z���X���Ƃ͎v�����A�����Ǝw�����Ă��錸�_����������Ȃ��B
�S���������Ă�q�ɂƂ��Ă͖��f�Șb�Ȃ��A���������q�͕K���������ˁB
�ԈႦ�����Ă������q�������o����Ȃ�t�c�[�Ƀo�c�ɂ��������
����ɂ���Đ������F�����ł���悤�ɂȂ�̂�����傢�Ɍ��\�Ȃ���
������܂܁u���ׂāv�������ĔF�����������@����Ȃ������ǂ��Ȃ�
�Ȃ��
�u3�g�̕ӂ̔䂪���ꂼ�ꓙ�����v
���ƃ_���Ȃ�
�܂��g3�g�̕ӂ̔�h�Ƃ�
a:p�Ab:q�Ac:r
�Ƃ���
�����悤���Ȃ�
�g�������h�Ƃ͑����g�������h���W�Ȃ̂����炱��3�g����Q���Ƃ����̊W
a:p �� b:q�A b:q �� c:r�Ac:r��a:p
��3�̓W�ɂ��ďq�ׂĂ�Ƃ����������Ȃ��A�����ăR����̊W���g�������h�Ƃ�
a:p = b:q�A b:q = c:r�Ac:r=a:p�d①
���������Ă�Ƃ��������悤���Ȃ����A������k�����̈Ӗ��ŏ����Ă��낵
����①�ɂ��āu�S�ē������v�Ɩ������Ȃ��ƃ_���Ƃ����Ȃ�g3�ӑ����h�̂Ƃ���
a = p�Ab = q�Ac = r
�̂Ƃ����g�S�āh�����Ȃ��ƃ_���ɂȂ�
3�ӂ̔�̂Ƃ��̓_����3�ӑ����̂Ƃ��͏ȗ��ł͘b�̒��낪����Ȃ�
>>965
�u(3�g�̕�)�̔䂪�������v�Ɖ��߂����a:b:c=p:q:r�ɂȂ邩��Ba:p=b:q=c:r�Ɠ��l�Ȃ��ǁA�����̒�`�͑O�҂Ȃ�B
����Ɓu3�g�̕ӂ����ׂē������v��a=b=c=p=q=r�Ǝ��邩��A�����́u���ꂼ��v���������B >>967
�u�����̒�`�͌�ҁv�ł����B �����������������m���ɖ������Ă��炢�������A�Ƃ����̂Ȃ烏�U���U���������������K�v���Ȃ������A�Ƃ������ƂɂȂ�B�ua:p=b:q=c:r�A����đ����v�ŁB���ۑ�w�����Ȃ炱���OK�ł���H(�m���)�B���w���̏ؖ��ł͓����������������łǂ̂悤�ȑ������������Ă��邩�܂Ŗ������Ȃ���Ȃ�Ȃ��Ƃ������[���Ȃ���d���Ȃ��B
a:b:c=p:q:r��a:p=b:q=c:r���ĈႤ�́H
�����Ӗ����Ǝv���Ă��B
�Ⴄ�Ȃ��������ĉ������B
>>967
> �u(3�g�̕�)�̔䂪�������v�Ɖ��߂����a:b:c=p:q:r�ɂȂ邩��B
���̉��߂͑����������H
�ł��Ȃ��Ȃ�����
�܂�g3�g�̕Ӂh���g�R�̕Ӂh�Ɠǂ܂Ȃ��Ɛ������Ȃ����ǁg�R�̕Ӂh���g3�̕ӂ̂Ȃ��g�h�Ɠǂ��
�@�h(3�g�̕�)�̔�h�@���@�g3�ӂ̑g�̂Ȃ���h
�Ɠǂݑւ��ď��߂Đ����������
���߂āg3�g�h���g�O�g�݁h�Ȃ�M���M����������ǂݑւ������ǁA����ł��g�ӂ̂R�g�h�Ȃ�Ƃ������g�O�g�̕Ӂh�ł͌ꏇ���`���N�`�����H
����Ɂu���������Ӗ��ɂ��Ƃ�邩��_���v�Ƃ����w���ɂ̓f�����b�g������
��Ɉ�ӂɂ������Ȃ����͂������Ƃ����̂͌����ɂ͌��E������A������x�u�����������������ꂽ�炱�����̈Ӗ��ɂƂ�̂��ӂ��v�Ƃ����̂������Ă����Ȃ��Ƃ����Ȃ�
�g3�g�̕ӂ̔�h�Ƃ������t�̕��тȂ�ʏ�g3�g�́g(�ӂ̔�)"�̌ꏇ�ʼn��߂���̂����ʂ��Ǝv�����A���ۂ��̈Ӗ��ŏ����Ă�Q�l���Ƃ������蓾��A
�����������ʂɎg���Ă镁�ʂ̌ꏇ�Łg���������߂����邩��_���h�Ǝw�����邱�Ƃɂ͕��Q�����Ȃ� >>970
���l���Ă͓̂������Ă��ƁB��������B
>>971
����A������u���ׂāv�����Ȃ��� �ԈႢ���Ă̂̓i���Z���X���ƌ����Ă��(>>963)�B�ł��u���ꂼ��v�Ə������������ԈႢ�ɂȂ����Ⴄ����A�����āu���ׂāv�ƕK�������Ƌ������Ă�̂��ȂƁB >>965
�ua:p�Ab:q�Ac:r�����ꂼ�ꓙ�����v
�͂������ɕςł���B��������
a:p = b:q�A b:q = c:r�Ac:r=a:p�d①
���������Ă�Ƃ����͉̂��߂���B
�����͂���ς�
�ua:p�Ab:q�Ac:r�����ׂē������v
�Ƃ���̂����R�ł���B >>973
> �ua:p�Ab:q�Ac:r�����ꂼ�ꓙ�����v
> �͂������ɕςł���B
�����������Ƃ��ˁB
a:p���������āA
b:q���������āA
c:r��������
���ĈӖ��ɂȂ�B
�܂�a:p���������̎��_�łȂ�����Ęb����ȁB >>965
�Ȃ�ŁH
�g�S�ā~�~�h�͂���W���ɂ��Ă��̑S�Ă̌����~�~�Ƃ����Ӗ��ɂ����̂����H
����̌��Ȃ�g�S�ē������h�̂����炻�́g����W���h�Ƃ�{ a:p��b:q, a:q��c:r, b:q��c:r}�Ƃ���2���̑g�Ƃ����̂�Ȃ�
{a:b b:q, c:r}���S�ē����������̂܂܂Ƃ��Ă��܂���
a:p�������� ���� b:q�������� ���� c:r��������
�Ɩ��Ӗ��ȕ��͂ɂȂ��Ă��܂� >>977
������������Ǖs���R�ł�����Č����Ă�́B
�uA�Ƃa��C�����ꂼ�ꓙ�����v�Ȃ�Č����āuA�Ƃa�A�a��C�AC��A�����ꂼ�ꓙ�����Ƃ������Ƃ�����A3�Ƃ��������Ă��Ƃ��ȁB�v�Ȃ�ĉ��Ȃ���蕁�ʂ��Ȃ��ł���H�uA�Ƃa��C�����ׂē������v�ƌ����ł��啁�ʁB
�O�̂��߂�����x�����Ƃ����ǁA����͂��ׂĂ���ΕK�v���Ȃ�Č����ĂȂ���B�����Ă��Ӗ��͒ʂ�Ǝv���B�ł����ꂼ��͂�����������A�����������Ȃ��悤�ɂ��ׂĂƏ������Ă͎̂w���Ƃ��ăA�����Ȃ��Č����Ă��B
�Ă����������J��Ԃ��Ă��B�ӌŒn�ɂȂ�Ȃ���ȁB >>979
�C���A�s���R�ł͂Ȃ�
�ǂ��炩�ƌ����Ƃ��̕����{�`�������R�Ȃ�
���̂Ȃ炻�������g�S�������h�́g�S�Č݂��ɑ��������h�̏ȗ��ł����Ȃ�
�g�S�ā~�~�h�͂���W���̌����S�ā~�~�Ƃ��������������Ɏg����̂��{�`�Ȃ̂Łg�S�ē������h��{a:x, b:y, c:z}"�Ƃ����W���ɒ��ڎg���͈̂Ӗ����ʂ�Ȃ�
���X���̏ꍇ�́g�S�ē������h�Ƃ����̂��u�S�Č݂��ɑ��������v�Ƃ������t�̏ȗ��Ƃ������߂ł��Ȃ��A����������g�S�Č݂��ɑ��������h�Ƃ����̂��߂�ǂ���������g�S�ē������h�Ƃ����ȗ��������������F�߂��Ă��邾��
������{a:x, b:y, c:z}���S�ē������Ƃ�{a:x=b:y, c:z=a:x, b:y,=c:z}���S�Đ�������Ƃ��������ȗ����Č����Ă���Ƃ����������ł��Ȃ��A����͕s���R�ł��Ȃ�ł��Ȃ��A�ނ��낱�����̕��������I�ȉ���
�����s���R�ł���Ǝv���Ă��܂����o�̕����ȗ��`�ɂȂ肫���Ă��邾��
����������w���w��ł��������ɂ��������ȗ��������\���Ɋ���Ă����̂͂������ǁA�u�ȗ��`�̉��߂̕������R�v�Ǝv���̂̓_�����Ǝv���A�����Ă����͏��w���̊��o�̕����D��Ă���ꍇ���炠��
��l�͂��܂�ɂ��ȗ������ꂽ�\���̕����悭�g�����炱�����̕����g���R�h�Ǝv���Ă��܂��̂͂��傤���Ȃ����ǁA����͖{���s���R�Ȋȗ��\���ł����Ȃ� ���ꂼ����Ă̂͊e�X���Ă��ƁB
3�g�̕ӂ̔䂪���ꂼ�ꓙ�����Ƃ������Ƃ́D�D�D
�܂��ӂ̔䂪3�g����܂��i��@A:P, B:Q, C:R�j�B
����3�g���ꂼ�ꂪ�������Ƃ������ƂɂȂ�܂��B
�����AA:P���������āAB:Q���������āAC:R���������Ƃ������Ƃł��B
�Ӗ��s���ł��B
>>977>>980�́u���ꂼ��=�S�āv�Ǝv���Ă���̂� �g���ꂼ��h���g�S�āh���W���Əq����Ȃ�����
�{��
���̏ꍇ�́g�W���h�Ƃ͒��ړI�ɂ�
{a:p, b:q, c:r }
�ŏq��́g�������h�ł��̂܂ܓK�p�����
a:p �͓������Ab:q�͓������Ac:r�͓�����
�ƂȂ��ĈӖ��s���ɂȂ��Ă��܂��A�Ӗ��s���ł���̂͂�����̏ꍇ�́g���݂��Ɂh�Ƃ�����
�܂�{a:p, b:q, c:r }���瑊�݂��ɓI��œ����閽��
{ a:p = b:q, a:p = c:r, b:q = c:r }
���S��������
�Ƃ����{�`�I�ɂ͉��߂ł��Ȃ��A�����猵���Ɍ��t���ȗ����Ȃ��ŏ�����
�u{a:p, b:q, c:r }�݂͌��ɑ��������v
�ƂȂ邵���̈Ӗ��ɂƂ�̂����`���
>>980
�͂��͂��A���������B
���Ⴀ���́u���O�p�`�Ƃ�3�̕ӂ����ꂼ�ꓙ�����O�p�`�ł���v�Ƃ������ĂȂ�B
����͂���ȕςȌ��������Ȃ����ǂˁB >>985
�������Ȃ�
�I���͂������̕����s���R���ƌ����Ă��
�Ȃ�ŕs���R�ȕ��g����
�u�s���R�����ǂ߂�ǂ��������ɂ͏ȗ����鎖��������Ă�ꍇ������v�Č����Ă�̂ɁH
�N�͎������s���R���ƌ����Ă�����I���Ɋ��߂Ă�� >>986
�ǂ������s���R���͐l���ꂼ��̌���Z���X�̖��ł����ē���ǂ���������Ȃ���B���Ƃ���ł͌���Z���X���Ⴄ���Ă��Ƃ��ˁB�D���ɂ��Ȃ�B
����ƁA�����l�̂��Ɠ������Ƃ������݂̂��Ƃ��Ȃ���B�܁A������Z���X���낤�ˁB >>986
��H������Ƒ҂Ă�H
���������āu���O�p�`�Ƃ�3�̕ӂ����ꂼ�ꓙ�����O�p�`�ł���v���s���R�ƌ����Ă�H
���ꂶ�Ⴀ�̌�����(�u3�����ׂē������v�͖{���u3�����ꂼ�ꓙ�����v�Ə����ׂ�)�Ƃ͋t����H���v�H ���n�I�����Ȍ��t�I�т�
����I���ʂȌ��t�I�т�
�̘b�ɉ߂������܂ł����܂ł��K�`���K�`���K�`���K�`�����邹����
���O�炪���܂ł����܂ł��K�`���K�`���K�`���K�`������Ă�
�ǂ�����Ď���X���҂Ō�����A�Ȃ�Č�����C�ŋ����A�q���ɗ@����C�ŋ����H
�X�������������Ă�˂���A������l������Ă患
>>981
3�g�̕ӂ̔䂪����ԓ������Ƃ������Ƃ́D�D�D
�܂��ӂ̔䂪3�g����܂��i��@A:P, B:Q, C:R�j�B
����3�g����Ԃ��������Ƃ������ƂɂȂ�܂��B
�����AA:P���������āAB:Q���������āAC:R���������Ƃ������Ƃł��B
�Ӗ��s���ł��B
�Ƃ������������� >>989
����I�Ȍ����Ƃ��Ă̓A�����������ɂ͊ԈႢ������_�����Ęb����Ȃ��ł��� �O>>847
>>888
�^�������ɂ��ƁA
�����3����������B
8�~3=24
���Ƃ͉ߕs�����E�B
��24 �������āu�������v�A���邢�́A�O������āu�S�ē������v�͈�a���Ȃ����A
�O������āu�������v�A���邢�́A�������āu�S�ē������v�͈�a������A�Ƃ����b���������͂��Ȃ̂����A�A�A�A�B
������A�ߑO���ɐႪ�~��n�߂��B
��͂˂Ɉ��̃y�[�X�ō~��B
����Ԃ����߁iAM12���j�҂�����ɓ����o���A1���Ԃ�2�}�C���̏�����������A�����1���Ԃ�1�}�C���̏�������������B
��͂��~��n�߂��H
>>990
�����Ȃ��ȁB
A:P�Ƃ�����ƁAB:Q�Ƃ�����ƁAC:R�Ƃ����䂪
�������Ƃ������ƂɂȂ�B
�����AA:P = B:Q = C:R �ł���B >>993
���O������āu�������v�͈�a������A�Ƃ����b���������͂��Ȃ̂����A�A�A�A�B
�O�g�̕ӂ̔䂪�������Ɉ�a��������Ƃ����b���Ă�l�͂��܂���
�O�Ӕ䑊���Ƃ������t�Ɉ�a�������ɂ��Ă�l�����܂��� >>998
�����_�u�X�^����B
����͌�����B����͌����Ȃ��B���ꂼ��ɓ����͂���Ɍ��܂��Ă邾�낤�B
�����A���ꂼ��̈Ӗ���������Ȃ��l���������B 905�͂Ƃ�ł��Ȃ����̂𓊉����Ă����Ȃ�
lud20230202020754ca
���̃X���ւ̌Œ胊���N�F http://5chb.net/r/math/1653324466/�q���g�F5ch�X����url��
http://xxxx.5ch
b.net/xxxx �̂悤��
b�����邾���ł����ŃX���ۑ��A�{���ł��܂��B
TOP�� TOP�� �@
�S�f���ꗗ ���̌f���� �l�C�X�� |
>50
>100
>200
>300
>500
>1000��
�V���摜
�@���u�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 59 YouTube����>3�{ ->�摜>33�� �v�������l�����Ă��܂��F
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 51
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 57
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 61
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 56
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 52
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 60
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 58
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 55
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 53
�E�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 54
�E�咆�w�Z�̓���1���ڂ̎Z���Ɨ��Ȃ̖�肪���J�@�P���������͉�����H
�E�����{�œ�ւ̓咆�w�Z�̓���1���ڂ̎Z���̖�肪���J�@���O��͉�����H
�E���E�̏����w���̗����w�͒����A���{�͎Z���E���w�łT�ʈȓ������w���Ȃ͂U�ʂɃ_�E�� [���ꁚ]
�E�����w���̍D���ȋ���1�ʂ́u�Z���E���w�v�ł������ȋ���1�ʂ��u�Z���E���w�v�����ӕs���ӂ̓�ɉ��i�� [�f�r���]�A��]
�E���w���w�̖������Ă���ǎВ{��肷���Ċw�Z�̑S�ē��e�Y��ĉ��������S�R�킩���
�E�y���n����z�u�����̂�2�{�̑Ίp���A�ǂ��炪�����H�v���w���̐������ɏՌ��c�Z���E���w�̊ԈႢ���Ȃ��q�ǂ����� [���炢�ށ�]
�E�y���w�O�N�z���w�̖��̉������������낭������
�E���w�Z�̎Z�������w�Z�̐��w�Ő��ђ����������z������������������
�E�y�Љ�z�����w�Z�̉^����A�l���̖��ŃJ�����������֎~�Z��
�E�����l�u���{�̏��w�Z4�N�̎Z���̖�肪������ėo�Ă����c�v�@�����̔���
�E���������w4�N���̟N��C�������A�A���`�ɗ��܂�u���O������x�ށ@�}�g��w�������w�Z�̎Z���̖��ɋ��
�E���������w4�N���̟N��C�������A�A���`�ɗ��܂�u���O������x�ށ@�}�g��w�������w�Z�̎Z���̖��ɋ��
�E�y�ߕ�z�@�g���b�R�����e�[�}�Ɏ��Ɓ��ی�҂��u�`��@�����w�Z�Z�����Ӎ߂�
�E�y�摜�z�����̒��w�Z�̐��w��肪���������@���ꂪ������ΊԈႢ�Ȃ��V��
�E�y�e���r�z���ۗ���@���w���̂��뒆�w���ɗ��܂������w�̖��ł������g���ށh [���S������]
�E�y����z���������w�Z���l���w���u�R�O�l��ڎw���v�@�����c���ȑ� [�Ǎ��̗��l��]
�E�y����z �����k���s�A�����w�Z���H�̐H�c�����莋�@ �����E�ی�҃A���P�[�g���{�����P��
�E���ʂ̂�5�l���A1�l���́u�g���b�R���v�@�����w�Z�Ŏ����ɂ��������ŕی�҂��玶���Ă��܂�
�E�����w�Z���H�ɏܖ�������{���@�����̋ƎҁA�Œ��S�J���� �Ǝҁu�i���I�ɂ͖��Ȃ��Ǝv�����v
�E���}�}�A�����w�Z�ւ̃P�[�^�C���������ɖҔᔻ�@�u����B���ۊm�F���ړI�Ȃ�A�V���o�[�l�ނ��ق��ȂǕ��@�͂���v
�E���w2�N�̐��w�̖������ā`
�E���w���ł������鐔�w�̖����o���Ă�
�E���w�Z�̎Z���̖��A�l�p�`�̖ʐς��u���~�c�v�Ōv�Z������O�p�ɂȂ����B���������Ă邩�킩��
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�5
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�2
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�9
�E�����̒��w�������ɏo���ꂽ�_���I�v�l�\�͂�₤���w�̖�肪�������Ƙb��ɂ���������������������������
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�8
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�7
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�12
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�11
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�10
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�4
�E�y���M�����z���ʂ̂�5�l���A1�l���E�E�E�B���ƂŁu�g���b�R���v�B�⍑�s�̏����w�Z���ی�҂ɎӍ߁�6
�E�5�l�����Ȃ��邩�1�l�����Ȃ��邩������w�Z�̎��ƂŢ�g���b�R��裁��ی�҂ɢ�q�����s�������Ă邶��Ȃ����I��ƍR�c����w�Z���Ӎ�
�E�����Ăق������w�̖��̉摜��\�����X��
�E�咆�w�Z�̓�����1���ڂ̎Z�������J�@���O�������H
�E�咆�w�Z�̓�����1���ڂ̎Z�������J�@���O�������H
�E�y �����w�Z�z�S���w�̓e�X�g�@�Ȋw�̋������߂���Ƃ� [�k��做]
�E���w�Z�̖�蕶���`���܂��傤�@���w�Z���`���Ȃ����@���Z���`����@��w���`����
�E��l�E�Љ�l�̎Z���E���w��蒼�� PART 1
�E���w�̖��̏o�T�������Ăق���
�E���̐��w�̖��̉��������ڂ���������
�E�^��w��������̐��w�̖��̉�����
�E���w�p�̎Z���ł�����z�����w�Z�̎��Ƃ����ʼn�����
�E���̐��w�̖��̉�����肢���܂��B�����Ȃ��ł�
�E���̒��w�Z�̋K�����̖�蕪��������܂����H
�E�V���K�|�[���̏��w�Z�ŏo�����Z���̖��������Ă��� [���f�]�ڋ֎~]
�E�y�N��z�}��u��������w�̎��Ɨ������ɂ���A�����w�Z���H���������v
�E��֒��w�̓����������Ă݂����Ǐ��w��������Ȃ̂킩��̂����Ă������炢������B�Z���Ɨ��Ȃ͂܂���������������B
�E���w�Z�����w���w�̒m���ŒP���Ɂu����Ȃ̏K���������H�v���ĂȂ�悤�Ȃ���ȍ~�܂������g��Ȃ��m���Ƃ��������狳���Ă���
�E�y����z���������w�Z�����̕��ώc�Ǝ��Ԃ�1������100���Ԉȏ�A�������u�x�e���ԃ[���v�c���É���w�̒����Ŕ��� [�{��������]
�E�y�Љ�z�����w�Z���H�ɂP���U�O�O�O�~�̃X�e�[�L�@���ꌧ���ǒ�
�E���c�j�R���@�����w�Z�̃X�}�z�������݁u����B�e�������ߖh�~�ɂȂ�v
�E�y����z���������@�����w�Z�ւ̃X�}�z�������݂Ɂu�����X�}�z�̎��̑����A�����߂̉����ɂȂ�v
�E���ɐ��w�̖����o���X��
17:46:42 up 7 days, 4:10, 0 users, load average: 9.28, 9.42, 9.69
in 2.4862821102142 sec
@2.4862821102142@0b7 on 121907
|
































